浅谈初中数学辅助线之妙用

陈红光 朱月祥

【摘要】在初中数学的几何问题中，人们解决这类型的题目往往会用到辅助线.添加辅助线是为了更好、更方便地解决问题.因为题目中给出的已知条件一般解决不了问题，而通过添加辅助线，便会得到一些新的条件，非常有助于解决问题，这是初中生在解决初中几何问题时的有效策略.因此，遇到困难的几何体时，辅助线来帮你！我们需要学会巧妙地利用辅助线.

【关键词】初中数学；辅助线；方法；妙用

众所周知，添加辅助线给几何题的解决有着不可忽视的地位.由于题目的变化无穷，所以辅助线的添加方法也是形形色色的.粗略地看那些辅助线似乎没有条理，无据可依，其实不然.在众多的几何题中，必然会存在着两样东西，一是图形，二是条件，也有隐含的条件.因此，我们作辅助线时可以根据图形的特殊性和条件的特殊性进行添加，这样题目将会迎刃而解.本文将针对初中几何题目，谈谈辅助线的妙用.

一、辅助线在三角形中的妙用

辅助线在三角形中的添加，是根据不同的问题作出不一样的辅助线来.如：

（一）在直接证明不出三角形三边关系时，可以延长某边或者是连接两点，构成三角形，从而使得结论中出现的线段在一个或多个三角形中，最后运用三角形三边的不等关系来证明.

（二）在直接证明不出三角形的外角大于任何和它不相邻的内角时，可以延长某边或者连接两点，构成三角形，使得小脚位于这个三角形的内角，要证明的大角在三角形的外角的位置上，最后利用外角定理求解.

（三）题目中有出现角平分线时，一般是在角的两边取相同的线段，从而构造全等三角形.

（四）题目中有出现以线段中点为端点的线段时，一般是延长加倍这条线段，从而构造全等三角形.

（五）题目中有出现三角形中线时，一般是延长加倍中线，从而构造全等三角形.

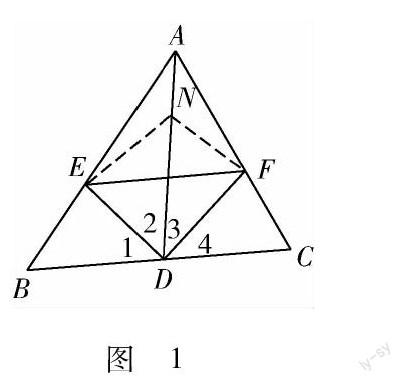
图1例如：如图1，已知AD为△ABC的中线，且∠1=∠2，∠3=∠4，求证：BE+CF>EF.

分析要证BE+CF>EF，可利用三角形三边关系定理证明，须把BE，CF，EF移到同一个三角形中，而由已知∠1=∠2，∠3=∠4，可在角的两边截取相等的线段，利用三角形全等对应边相等，把EN，FN，EF移到同一个三角形中.

证明在DA上截取DN=DB，连接NE，NF，则DN=DC，

在△DBE和△DNE中：

∵DN=DB（辅助线的作法），∠1=∠2（已知），ED=ED（公共边），

∴△DBE≌△DNE（SAS），

∴BE=NE（全等三角形對应边相等）.

同理可得：CF=NF.

在△EFN中EN+FN>EF（三角形两边之和大于第三边）

∴BE+CF>EF.

点评当题目中有角平分线时，通常可考虑在角的两边截取相等的线段，构造全等三角形，然后用全等三角形的性质得到对应元素相等.

二、辅助线在平行四边形中的妙用

正方形、矩形、菱形都属于平行四边形，它们的两组对角、对边以及对角线都具有一些相同的性质，因此，给这些平行四边形添加辅助线时的方法是差不多的，都是为了让线段垂直或平行，然后构造出全等或相似的三角形.一般常用的方法是连接对角线、平移对角线，延长一边中点与顶点的连线等，这样可以将平行四边形转化成三角形、矩形等图形，有利于解决问题.

三、辅助线在圆中的妙用

在圆中添加辅助线的办法通常有：

（一）可以根据垂径平分定理，过圆心作弦的垂线.

（二）可以根据同圆或者等圆中的圆心角、圆周角、弦、弧的相互转换关系，连接圆上相关的点来解决问题.

（三）当题目中有直径这一条件时，通常考虑“直径所对的圆周角是直角”来添加辅助线.

（四）当题中有切线时，通常连接过切点的半径或直径，利用切线与它垂直的特点.有时也作过切点的弦，沟通弦切角与圆心角、圆周角之间的关系.

（五）当题中有两圆相切时，首先考虑的是过切点作两圆的公切线，由此沟通弦切角与圆周角之间的联系.有时也作两圆的连心线，利用切点在连心线上沟通圆心距与两圆半径之间的关系.

（六）两圆相交时，作两圆的公共弦，以两圆的公共弦作为“桥梁”沟通两圆的圆周角和其他角之间的关系.

总而言之，在几何题中添加辅助线是有规律可循的，学生需要对这些图形添加辅助线作一个系统的归纳总结，这样才能开拓思路，提高解决几何题型的技巧.

【参考文献】

[1]徐青.几何问题解决的图式水平及其特点研究[J].安阳师范学院学报，2012（01）.

[2]王娜.辅助线对高中生解决空间几何问题的影响[D].河南大学，2012.

[3]宋蓓.初中数学解题策略的研究及应用[D].天津师范大学，2013.