对一道中考压轴题的分析与思考

李小兰

[摘要]代数与几何图形的综合题是初中生学习数学的一个难点，也是中考的一类热点问题.而运用数形结合方法解题是一个比较好的途径.主要针对学生解题的失误，结合了一些例子分析了数形结合在数学教学中的应用，对教师的“教”和学生的“学”有很好的促进作用.

[关键词]中考压轴题 思考 数形结合

[中图分类号] G633.6 [文献标识码] A [文章编号] 16746058（2015）080045

2011年又一次课改后，各省的中考压轴题很大程度上都围绕着函数展开命题，如何将函数问题考出特色，考出新意，成了命题者不懈的追求.2012年玉林市数学中考试卷第25题正是朝着这个方向努力，并且做到了初中代数与几何的综合考查.只可惜阅卷结果令人痛心，大部分考生只在第一个问题上得分，个别考场没有一个考生着笔第二、三个问题.许多考生在解题中出现很多问题，这值得我们教师深思.笔者也走访了本县的部分毕业班，发现了一些问题，下面通过反思师生的失误反观我们的教育教学.

一、题目呈现

【例1】 如图1，在平面直角坐标系xOy中，梯形AOBC的边OB在x轴的正半轴上，AC∥OB，BC⊥OB，过点A的双曲线y=kx的一支在第一象限交梯形对角线OC于点D，交边BC于点E.

（1）填空：双曲线的另一支在第 象限，k的取值范围是 ；

（2）若点C的坐标为（2，2），当点E在什么位置时，阴影部分的面积S最小？

（3）若ODOC=12，S△OAC=2，求双曲线的解析式.

二、解析

（1）由概念得出答案：三，k>0.

（2）由点C的坐标为（2，2），可得A点的坐标为（k2，2），E点的坐标为（2，k2），∴S阴影部分=S△ACE+S△OBE=18（k-2）2+32，可求E点的坐标为（2，1），即当点E在BC的中点时，阴影部分的面积S最小；

（3）设D点坐标为（a，ka），可得C点坐标为（2a，2ka）和A点坐标为（a2，2ka）.∵S△OAC=2，得12×（2a-a2）×2ka=2，解得k=43.

三、错误分析

（1）此题的第二个问题应该属于中档难度的题目，可部分班级平时数学成绩优秀的学生却无从下笔，笔者归纳了访问到的教师和学生的一些说法，并进行了原因分析.

①生1：没见过此类题目，题目求三角形的面积却没给出任何线段的长度.

②生2：只知道点C的坐标为（2，2），没有办法求出点E和点A的坐标.

③师：学生函数题目练了很多，但就是不懂利用坐标求线段长.

分析：本题蕴含了数形结合的思想方法，数形结合是解决此题的关键.由于几何图形与函数图形结合在一起，学生分析问题需要进行“几何图形——数量关系——函数图形”之间的互相转化.同时考虑到动静转换原则，此题可以把动态的点E想象成静态的点E，即得点E的坐标为（2，k2）.学生在平时的学习中没有归纳总结解题方法，教师在教学过程中也没有着重培养学生的数形结合思想，导致学生在考试中失分.

四、教学思考

笔者有幸参加了当年的中考阅卷，这道题得分率较低的情况值得我们深思，根据这类问题的错误分析，我们应在教学中采取相应的策略.

1.培养学生数形结合的解题意识

在课堂教学中，注意选择一些非常典型的、能很好地发挥数形结合思想方法优势的例题进行讲解，在精讲过程中，注意用问题引导学生运用数形结合思想方法解题.讲解完毕后，还可以对数形结合思想方法进行总结和反思.通过对一道题的总结和反思，我们得到一类问题的解题方法，从而大大深化了我们对知识的理解，丰富了我们的知识，提高了我们的解题能力.

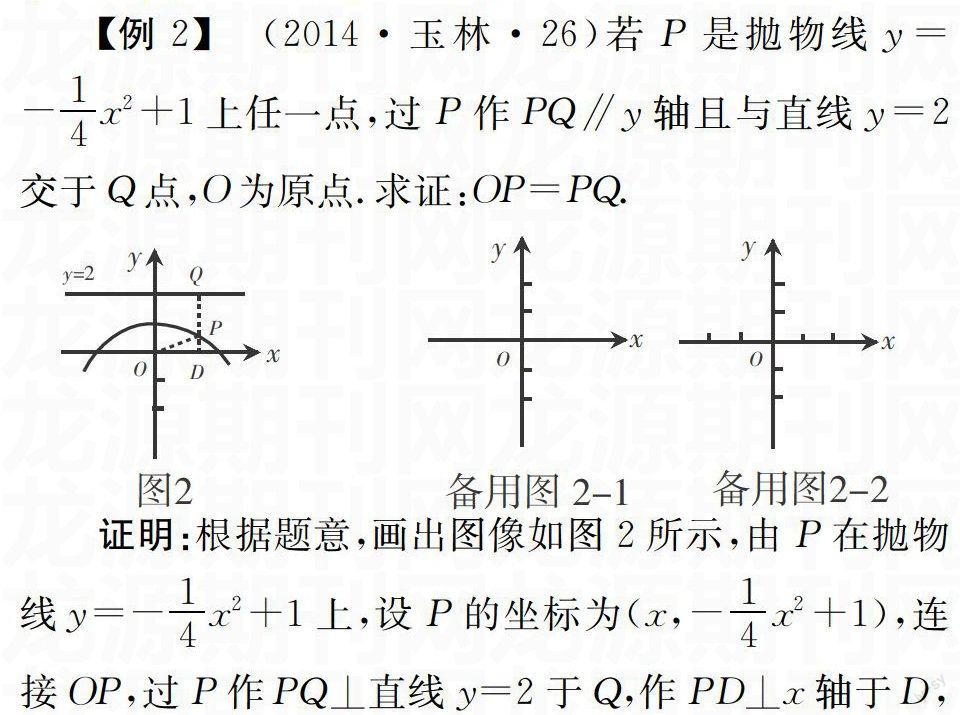
【例2】 （2014·玉林·26）若P是抛物线y=-14x2+1上任一点，过P作PQ∥y轴且与直线y=2交于Q点，O为原点.求证：OP=PQ.

分析：此类题目是以形助数的几何问题.首先应画出大致的示意图.发现图中几何条件较少，所以考虑用坐标转化求出OP、PQ的值，再进行比较.这里也有数学技巧，讨论动点P在抛物线y=-14x2+1上，则可设其坐标为（x，-14x2+1），进而易求OP、PQ.

2.数形结合求解问题的主要途径

利用数形结合求解问题，必须采取一定的切入途径，这是解题得以成功的重要保证，这里我们只介绍罗增儒的观点.

罗增儒在总结了数式与图形对应的基本数学方法基础上提出了三个主要途径：①通过坐标系、直角坐标系；②转化；③构造.

【例3】 （2014·湖南岳阳）如图3，已知点A是直线y=x与反比例函数y=kx（k>0，x>0）的交点，B是y=kx的图像上的另一点.BC∥x轴，交y轴于点C.动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C.过点P作PM⊥x轴，PN⊥y轴，垂足分别为M，N.设四边形OMPN的面积为S，P点运动的时间为t，则S关于t的函数图像大致为（ ）.

分析：本题运用转化思想在“几何图形——数量关系——函数图形”之间互相转化，但关键是通过坐标系构造出动态的四边形OMPN，同时运用了动静转换原则，列出四边形OMPN的面积S与运动时间t的函数关系式，最后，由函数的图像得出答案B.

3.渗透数形结合思想，培养数学思维能力

（1）由数思形，培养思维的灵活性.思维的灵活性是指多方位、多角度思考问题的灵活程度.

【例4】 已知a、b均为正数，a+b=2，求a2+4+b2+1的值.

分析：这是一道代数计算题，单从代数方面思考显得深奥难解，而利用逆反原则则可“化数为形”，从而使问题快速获解.这样有效地提高了学生思维的灵活性.

分析：如图4，先画线段AB=2，在线段AB上截取AE=a，BE=b，过A作AC⊥AB，且AC=2，过B作BD⊥AB，且BD=1，则CE=a2+4，DE=b2+1，原题即求CE+DE的最小值.易得a2+4+b2+1=13.

（2）由形思数，培养思维的严密性.

【例5】 等腰三角形一腰上的高等于腰长的一半，求顶角的度数.

分析：因为题目中没有绘出图形，学生在画图时往往不能准确地理解题意，画出所有符合条件的图形，犯了“以偏概全”之错.此题学生往往会漏掉等腰三角形是钝角三角形的情况.因此，教师应有针对性地加强这方面的训练，促使学生逐步养成思维的严密性.

（3）数形兼顾，培养思维的创造性.

创造性思维是一种综合性思维.法国遗传学家F·雅各布说：“创造就是重新组合.”数形结合中，由数想形，可培养学生的联想解题思维；由形想数，可培养学生的创造性思维，激发学生的求知欲及学习兴趣.数形结合把发散思维和收敛思维有机结合起来，有利于培养学生的创新能力.

【例6】 如图5，在等腰梯形ABCD中，∠B=60°，PQ同时从B出发，以每秒1单位长度分别沿BADC和BCD方向运动至相遇时停止，设运动时间为t（秒），△BPQ的面积为S（平方单位），S与t的函数图像如图6所示，则下列结论错误的是（ ）.

A.当t=4秒时，S=43

B.当4≤t≤8时，S=23t

C.AD=4

D.当t=9秒时，BP平分梯形ABCD的面积

分析：本题考查了动线、面积、一次函数、二次函数的图像和性质等知识，解题的关键是利用数形结合思想、转化思想、分类思想、方程思想、函数思想、动静转换法等.

华罗庚先生说过：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休.”的确，数形结合是一种重要的数学思想和一柄双刃解题利剑.教师只有在平时的教学中落实数形结合思想的渗透，学生才能见数思形、见形思数、见形助数、以数辅形，真正利用好这柄双刃解题利剑，而不仅仅是为了做题而做题.让我们的学生从“题海战术”中得以解脱，真正实现素质教育.

（责任编辑 钟伟芳）