利用玀atlab探讨迭代算法

董华楠

【摘要】本文利用计算机，借助Matlab工具，对求方程数值解常用的二分法、不动点法和牛顿法进行探析比较，得出直观结论，为相关知识的理解和运用提供了依据.

【关键词】Matlab；方程数值解；迭代法

很多数学问题都可归结为方程问题求解，一般方程又很难求得其解析解，而处理某些实际问题时需要近似解即可，所以研究方程的数值解法是有效解决问题的关键.在求解非线性方程的方法中，迭代法是求非线性方程（非线性方程组）数值解的一种重要的方法.而二分法、不动点迭代法和牛顿迭代法等都是较常用的迭代方法.因此，深入了解和掌握不同迭代方法的特点与差别，有助于相关问题的解决.

引言

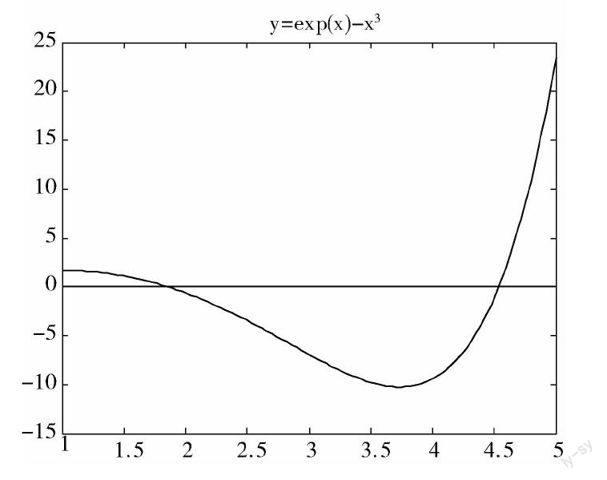
检验和比较不同迭代算法的常用方法就是针对特定模型（方程）进行迭代逼近计算，借助计算机是行之有效的手段.在此，通过编写Matlab程序，分别用二分法、不动点法和牛顿迭代法求非线性方程ex-x3=0的数值解，观察其逼近速度，进行比较分析，从而得出结论.

行的Matlab软件是安装在Win7系统下的R2011b版本.

由上表中的数字对比，可显然看出，三种迭代算法中，牛顿迭代法速度最快，不动点迭代法次之，二分法较慢.虽然在选取迭代初值或区间时有一定的主观因素，但基本上能反映出三种迭代法的主要差别.

四、结论

综合上述结果，同时结合三种迭代方法的各自结构特点，可以得出：二分法简单易用，对f（x） 要求不高，只要连续即可，但无法求复根及偶重根，且收敛速度慢，多用于为其他求根方法提供初始近似值；不动点迭代法逐次逼近，将隐式方程归结为显式计算，显式关系式的结构直接影响到点列的敛散性，选取不当则得不到方程的数值解（即使方程有根）；牛顿迭代法正是将局部线性化的方法用于求解方程，牛顿迭代法的最大优点是收敛速度快，具有二阶收敛.了解了三种迭代法的特点，便于有效地加以运用.

【参考文献】

[1]王家文，王皓，刘海.Matlab7.0编程基础[M].机械工业出版社，2005：143-154.

[2]苏金明，阮沈勇.Matlab实用教程[M].电子工业出版社，2005：94-101.

[3]于润伟.Matlab基础及应用[M].机械工业出版社，2003：107-112.