基于背景加权空间直方图的目标跟踪

刘 芳，余旺盛

（1.中国人民解放军空军94188部队，陕西 西安710077；2.空军工程大学 信息与导航学院，陕西 西安710077）

引言

视觉跟踪技术广泛应用于视频监控、智能交通、工业控制以及视觉导航等诸多民用和军事领域，是计算机视觉领域研究的热点和难点问题［1－2］。近年来，针对视觉跟踪技术的理论研究取得了快速的发展，常用的跟踪算法通常可以分为基于区域的跟踪［3］、基于特征的跟踪［4］、基于变形模板的跟踪［5］以及基于模型的跟踪等［6］。众多跟踪算法中，Mean Shift跟踪算法具有理论完备、原理简单以及性能相对稳定等优点，是视觉跟踪领域的重要研究内容。然而，传统的 Mean Shift跟踪算法［7］采用简单的颜色直方图模型对目标进行描述，导致算法容易受到背景颜色的干扰，鲁棒性降低。针对这一问题，Comaniciu等人提出了一种背景加权策略［8］，利用目标周围的背景信息对颜色直方图模型进行加权修正，以此提高目标前景的可分辨性。然而，Ning等人［9］指出如果同时对目标模型和目标候选模型进行加权修正，反而达不到预期的效果，并提出只对目标模型进行加权修正的改进背景加权目标跟踪算法。Birchfield等人［10］则从传统颜色直方图模型空间信息缺失的角度出发，提出了空间直方图（spatial histogram）概念，通过在传统颜色直方图模型中增加像素分布的空间矩特征，增强了颜色模型的特征分辨能力［11］。分析发现，背景颜色的干扰是影响跟踪鲁棒性的外因，目标模型空间信息的缺失是影响跟踪鲁棒性的内因。实际跟踪中，内外因通常同时起作用，对跟踪造成干扰。上述研究仅从单一角度出发寻求解决问题的途径，因此改进后算法的性能提升有限。对此，本文提出一种基于背景加权空间直方图模型，同时考虑影响跟踪鲁棒性的内因和外因，取得了较好的跟踪效果。

1 背景加权空间直方图

背景加权空间直方图的主要思路是将背景加权直方图与空间直方图进行融合，在空间直方图中引入背景加权策略，以提高特征的鲁棒性。

1.1 空间直方图

空间直方图是一种融合了像素空间分布高阶矩信息特征的直方图，由于引入了空间分布信息，其区分度得到显著增强。对于每一个直方图子区间，空间直方图需要统计3个信息：1）当前子区间内像素出现的频率；2）当前子区间内所有像素的坐标均值向量；3）当前子区间内所有像素坐标的协方差矩阵。空间直方图可表示如下：

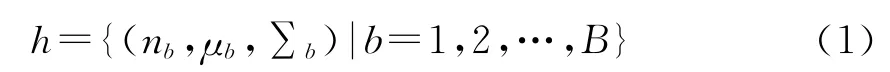
式中：B为空间直方图子区间的个数；nb、μb和∑b分别为子区间b中的像素出现的频率、像素坐标的均值向量以及协方差矩阵，其各自的计算公式如下［10］：

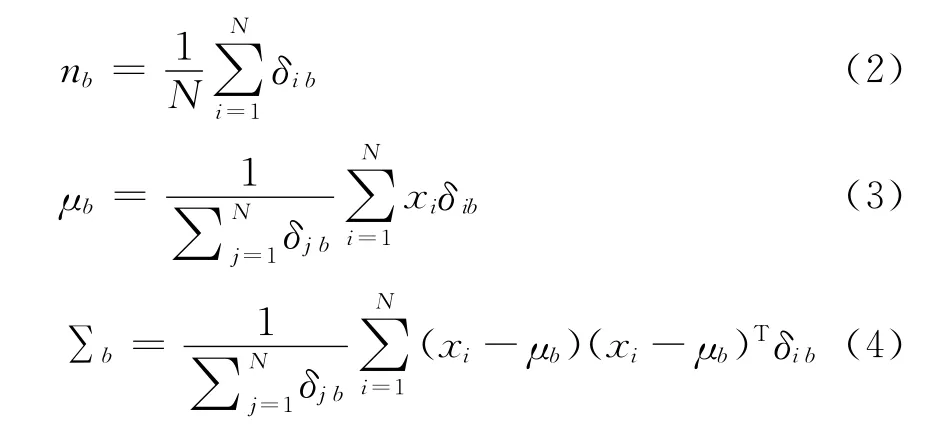
式中：N 为像素的个数；（3）式和（4）式中，xi为像素i的坐标。为适应图像中不同位置和大小图像区域的特征描述，需要将像素的坐标值进行归一化处理，即将所有像素的坐标值映射到［－1，1］区间内［12］。

1.2 背景加权空间直方图

为增强跟踪区域背景和前景的可区分性，

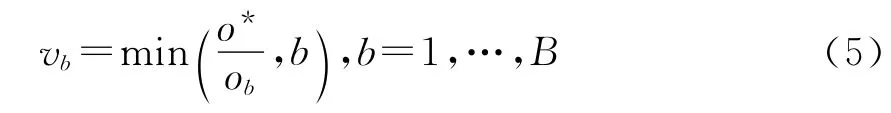
则利用背景权向量修正后的背景加权直方图可以表示为｛n′b＝C·vbnb｜b＝1，…，B｝，这里C 为归一化的常量。

由于背景信息仅对直方图的颜色分布造成干扰，因此对应于空间直方图，只需利用加权向量对直方图数据中的颜色分量进行修正，修正后的加权空间直方图可表示为

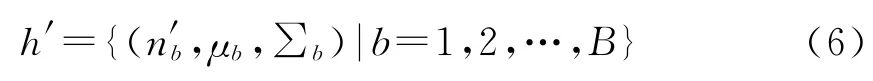
式中，n′b＝C·vbnb为修正后的颜色分量。

1.3 相似性度量

由于引进了像素的空间分布信息，空间直方图的数据结构在原有直方图数据的基础上发生了变化，传统的相似性度量方法不适应空间直方图的相似性度量。Birchfield等人在研究空间直方图的应用时提出了一种类似于Bhattacharyya系数的相似性度量准则。

对于空间直方图h＝｛（nb，∞b，∑）｜b＝1，2，…，B｝和h′＝｛（n′b，μ′b，∑′b）｜b＝1，2，…，B｝，其相似性度量可用如下公式表示：Comaniciu等人提出了一种背景加权策略。其基本思想是通过统计紧邻目标的背景区域内像素的颜色概率分布，计算出一组能够抑制目标中所含背景信息的权值向量，利用该向量对颜色直方图模型进行加权修正即可得到分辨率更高的目标模型。取3倍面积于目标的环形区域为背景区域，设｛nb｜b＝1，…，B｝和｛ob｜b＝1，…，B｝分别为目标和背景区域的归一化颜色直方图，计o＊为｛ob｜b＝1，…，B｝中的最小正数，定义如下权值：

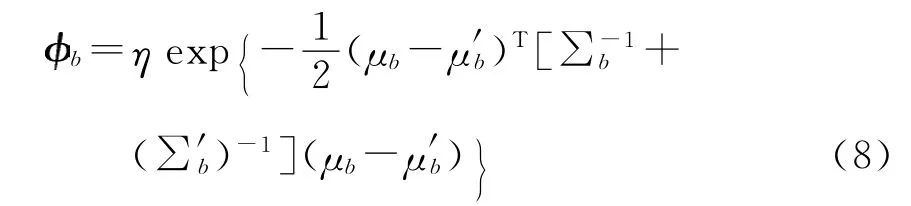
式中η为高斯归一化常量。

2 本文跟踪算法

2.1 基本原理

在跟踪视频的第1帧中以矩形框标定被跟踪的目标，计算目标区域的空间直方图和背景加权向量，得到背景加权直方图，记为q＝｛（nqb，μqb，∑qb）｜b＝1，2，…，B｝。依据Ning等人的研究结果，仅需对目标模型进行背景加权。假设p（y）＝｛（npb（y），μpb（y），∑pb（y））｜b＝1，2，…，B｝为以点y为中心的目标候选模型，其中：

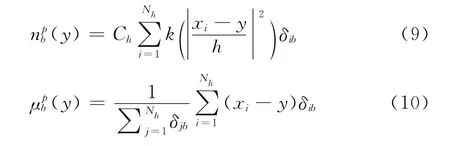
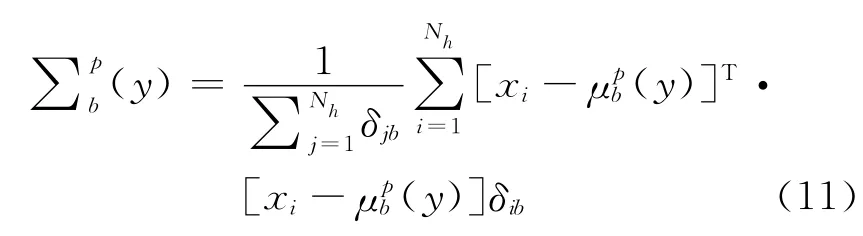
则目标模型与目标候选模型之间的相似性度量为

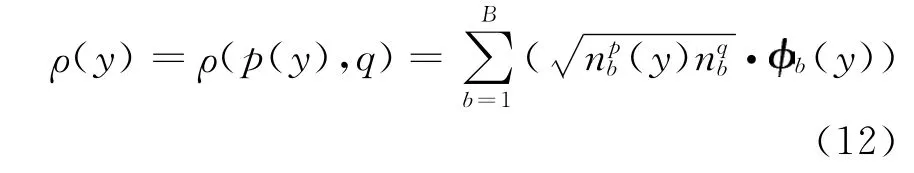
将ρ（y）在pb（y0）和μpb（y0）处进行二维泰勒展开可得：

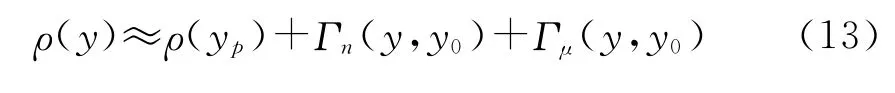
式中：

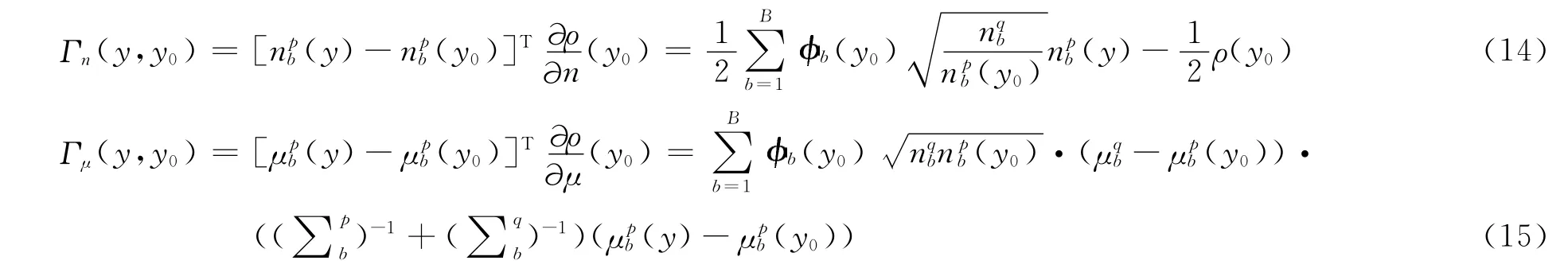
将上两式代入ρ（y），对y求偏导数并整理可得：

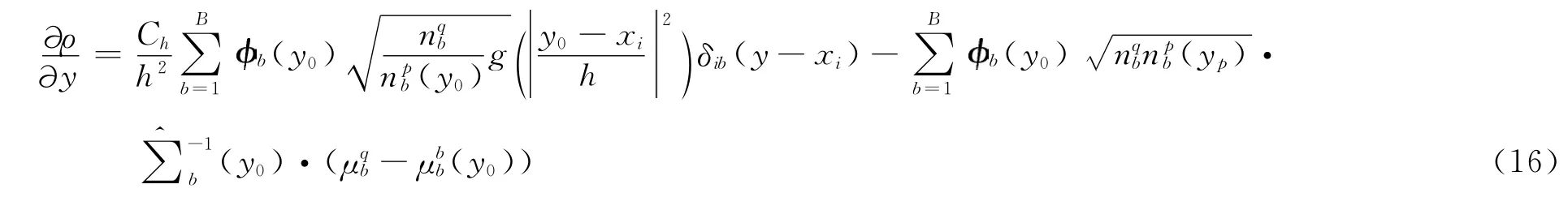
令∂ρ／∂y＝0，可得：

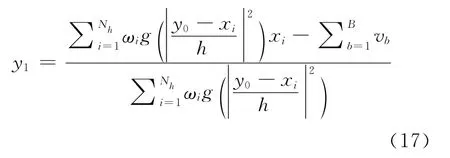
式中，

2.2 算法步骤

本文综合背景加权直方图与空间直方图各自的优势构建鲁棒的目标模型，在Mean Shift跟踪框架下实现对目标的跟踪。当视频输入时，在第1帧中标定需要跟踪的目标，记目标的初始位置为y1，以3倍于目标区域的环形区域为背景区域，计算目标区域的空间直方图和背景加权向量，得到目标的背景加权空间直方图，记为当下一帧输入时，开始跟踪流程，具体步骤如下：

第1步：在当前帧中，以y0为中心，计算与目标模板等大小图像区域的空间直方图，将其记为

第2步：将p（y0）的各分量代入（18）式和（19）式得到ωi和vb，进一步代入（17）式得到迁移后的新位置y1。

第3步：计算ε＝‖y0－y1‖，将其与预先设定的阈值ε0进行比较，若ε≤ε0，转至第5步；否则进入第4步。

第4步：若当前循环次数N达到预先设定的阈值N0，则进入第5步；否则，令y0＝y1，返回第1步。

第5步：以y1为当前帧中目标的最终位置，输出跟踪结果。

在跟踪的过程中，目标自身的颜色特征相对稳定，但随着跟踪的推进，目标所处的背景会发生较为明显的变化。因此定义模型更新规则如下：当前帧跟踪完成后，计算背景区域的归一化颜色直方图，将其与目标模型的背景颜色直方图进行相似性度量，若相似性度量值小于ε′0，则用当前背景区域的归一化颜色直方图更新目标模型的背景加权向量，进而对目标模型进行更新。

综上所述，本文算法与传统Mean Shift跟踪算法的本质区别是引入了描述空间分布信息的空间直方图，并通过背景加权策略进一步增强跟踪的鲁棒性。算法的具体流程如图1所示。

3 实验与分析

为充分验证本文所提算法的跟踪性能，选择了仅利用背景加权直方图的Mean Shift跟踪算法［10］、仅利用空间直方图的 Mean Shift跟踪算法［11］以及压缩感知跟踪算法［13］作为对照实验。文献［10］算法和文献［11］算法分别用于验证仅考虑背景干扰和仅考虑空间信息时的跟踪效果，文献［13］算法为近年来性能相对优越的跟踪算法。在本文实验中，参数ε0均设为0.1，迭代次数ε′0设为15。本文中模型更新的阈值参数ε′0设为0.6。实验采用的测试视频来自OTB2013数据库［14］，跟踪实验所采用的仿真平台为MATLAB2011。

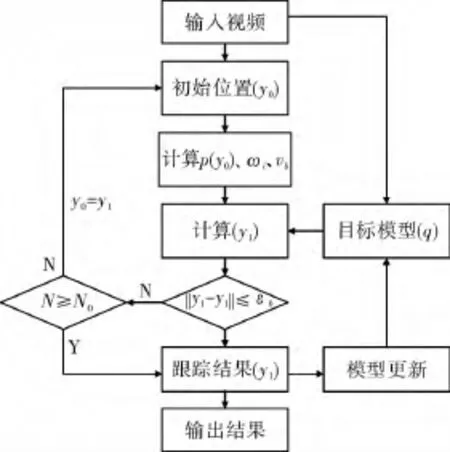
图1 本文算法跟踪流程图Fig.1 Tracking flow chart of proposed algorithm

3.1 实验结果

图2所示为本文算法与参考算法跟踪的部分实验结果，图中不同算法的跟踪结果以不同颜色的矩形框以示区别，其中文献［10］算法、文献［11］算法、文献［13］算法和本文算法依次为蓝色、青色、红色和绿色。

图2 跟踪的部分实验结果，自上至下依次为Basketball，Bolt，David3，MountainBike序列（彩图在网上）Fig.2 Some experimental results of tracking，the sequences from top to bottom are Basketball，Bolt，David3，MountainBike sequentially（colour images are online）

第1组测试视频为“Basketball”序列，跟踪目标为篮球运动员。由于球场上相似目标较多，给跟踪带来一定的难度。文献［10］中仅利用了目标所处的背景信息，当目标遇到相似背景干扰时则容易丢失目标，如第500帧、第600帧等。文献［11］中算法过分依赖于目标颜色的空间分布信息，导致跟踪算法在第500帧、第600帧中出现偏差。文献［13］算法的跟踪效果不够理想，在大多数结果中均出现了严重的偏差。相较而言，本文算法取得了更加稳定的跟踪结果。

第2组测试视频为“Bolt”序列，跟踪目标为短跑运动员。目标的快速运动以及相似目标的干扰是跟踪的难点。文献［10］和文献［11］中算法在前100帧中基本能够完成对目标的有效跟踪，但之后即逐渐偏离目标的真实位置，直至最终丢失目标。文献［13］中算法在跟踪开始不久后即丢失目标，跟踪失败，其主要原因是受到背景区域中相似目标的干扰。在该视频序列中，本文算法能够自始至终地以较高的精度完成对目标的跟踪。

第3组测试视频为“David3”序列，跟踪的目标为行人。目标的短时遮挡以及背景区域的相似颜色分布是跟踪的主要难点。文献［10］中算法过于依赖目标的背景加权分量，导致跟踪的效果不甚理想，一开始不久即丢失目标。由于目标的相对结构信息未发生明显变化，因此文献［11］算法取得了较为理想的跟踪结果。文献［13］算法采用的是Haar特征，目标与背景区域中汽车存在较为相似的特征分布，因此在跟踪的过程中受到干扰，如第150帧、第200帧等。

第4组测试视频为“MountainBike”序列，跟踪的目标为山地自行车运动员。目标的非刚性形变和低对比度是跟踪难点。文献［10］算法通过背景加权分量抑制了目标区域内的背景因素，取得了较为理想的跟踪结果。文献［11］算法整体跟踪效果较好，但在最后阶段受到目标非刚性形变的影响而出现跟踪偏差。文献［13］算法在图中第40帧之后的所有结果中均跟踪失败。

3.2 性能分析

为进一步对所提出的算法以及参考算法的跟踪性能进行定量分析，选择了跟踪中心位置误差［15］（center location error）进 行 评 估。 其 评估标准是跟踪所得结果与目标真实结果的中心位置之间的欧氏距离，距离越小，表明算法的跟踪精度越高，反之表明算法的跟踪精度越低。平均中心位置误差是对跟踪性能进行统计评估的指标，数值越小，表明跟踪综合性能越优。图3所示为所有算法对4组测试视频进行跟踪所得的中心位置误差比较曲线图。从图中可以明显看出，本文所提算法比参考算法具有明显的优势。

图3 跟踪结果的中心位置误差（单位：像素）比较Fig.3 Comparison of center location error of tracking results

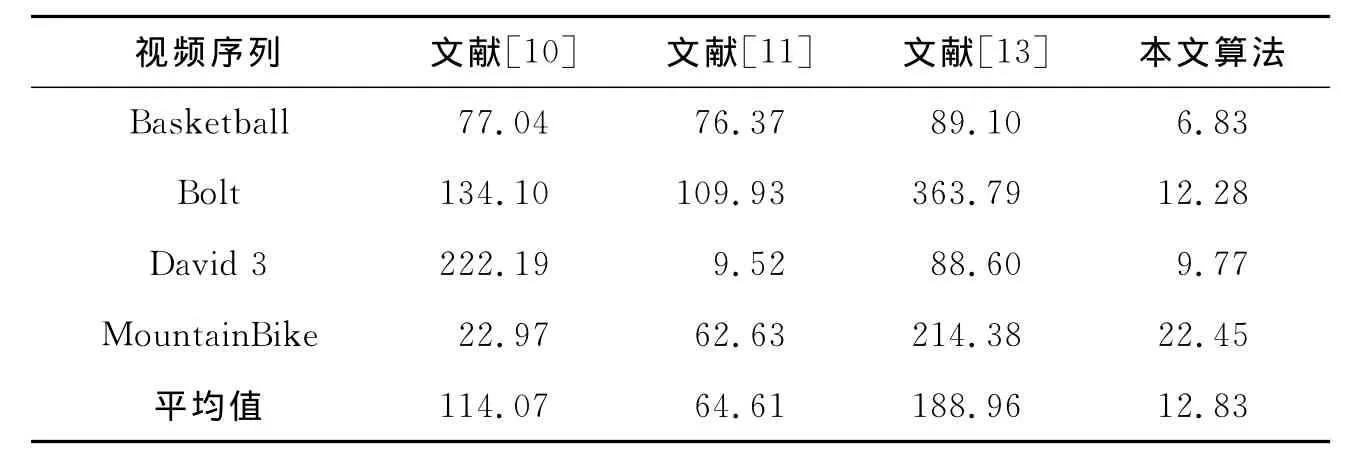
表1 跟踪结果的平均中心位置误差比较 像素Table 1 Comparison of mean center location error of tracking results

表1为几种算法所得的平均中心位置误差的比较，由表中数据可以看出，本文算法在Basketball、Bolt和 MountainBike序列中均取得了最优结果，在David3序列中取得了次优结果，表明本文所提算法比参考算法的综合跟踪性能更加优越。

在跟踪的时间开销方面，由于综合了2种特征，导致跟踪的效率较文献［10］和文献［11］算法略有降低，但总体上依然能够达到10fps左右。在编程实现时，文献［13］算法部分时间开销较大的环节采用了C＋＋优化，因此运行速度能达到19fps左右。跟踪时程序运行的具体速度如表2所示。由此可见，本文算法牺牲了一定的时间开销，以此获得了跟踪性能的提升。

表2 不同算法的跟踪速度比较 f／sTable 2 The comparison of tracking speed of different tracking algorithms

4 结论

本文提出了一种综合目标背景加权直方图和空间直方图的目标跟踪算法，针对二者的优势取长补短，完成了对目标的鲁棒跟踪。所提算法比采用背景加权直方图的跟踪算法具有更加优越的空间变化适应性能，比采用空间直方图的跟踪算法具有更加优越的背景抑制性能。仿真实验和定量分析结果表明，本文所提算法提高了跟踪的精度和鲁棒性，具有一定的理论意义。

［1］ Smeulders A W M，Chu D M，Cucchiara R，et al.Visual tracking：an experimental survey ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2014，36（7）：1442－1468.

［2］ Hou Zhiqiang，Han Chongzhao.A survey of visual tracking［J］.Acta Automatica Sinica，2006，32（4）：603－617.侯志强，韩崇昭.视觉跟踪技术综述［J］.自动化学报，2006，32（4）：603－617.

［3］ Henriques F，Caseiro R，Martins P，et al.Exploiting the circulant structure of tracking－by－detection with Kernels ［J］.Computer Science ，2012，575：702－715.

［4］ Li Xiangjun，Li Liangfu.Particle filter algorithm based on posterior probability measurement ［J］.Journal of Applied Optics，2011，32（4）：646－651.李向军，李良福.基于后验概率度量的粒子滤波跟踪算法研究［J］.应用光学，2011，32（4）：646－651.

［5］ Leymarie F，Levine M D.Tracking deformable objects in the plane using an active contour model［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1993，15（6）：617－624.

［6］ Leotta M J，Mundy J L.Vehicle surveillance with a generic，adaptive，3Dvehicle model ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（7）：1457－1469.

［7］ Comaniciu D，Ramesh V，Meer P.Real－time tracking of non－rigid objects using mean shift［C］.USA：IEEE Press，2000：142－149.

［8］ Comaniciu D，Ramesh V，Meer P.Kernel－based object tracking［J］.IEEE Transactions on Pattern A－nalysis and Machine Intelligence，2003，25（5）：564－77.

［9］ Ning J，Zhang L，Zhang D，et al.Robust mean－shift tracking with corrected background－weighted histogram ［J］.IET Computer Vision，2012，6（1）：62－69.

［10］Birchfield S T，Rangarajan S.Spatiograms versus histograms for region－based tracking ［C］.USA：IEEE Press，2005：1158－1163.

［11］Yao Zhijun，Liu Juntao，Lai Chongyuan，et al.An improved Jensen－Shannon divergence based spatiogram similarity measure for object tracking［J］.Acta Automatica Sinica，2011，37（12）：1464－1473.姚志均，刘俊涛，赖重远.一种改进的JSD距离的空间直方图相似性度量及目标跟踪［J］.自动化学报，2011，37（12）：1464－1473.

［12］Conaire C O，O'connor N E，Smeaton A F.An improved spatiogram similarity measure for robust object localization ［C］.USA：IEEE Press，2007：1067－1072.

［13］Zhang K，Zhang L，Yang M.Real－time compressive tracking ［C］.Berlin：Springer－Verlag，2012：864－877.

［14］Wu Y，Lim J，Yang M H.Online object tracking：a benchmark［C］.USA：IEEE Press，2013：2411－2418.

［15］Yu Wangsheng，Tian Xiaohua，Hou Zhiqiang，et al.Visual tracking algorithm based on feature matching of key regions［J］.Acta Electronica Sinica.2014，42（11）：2150－2156.余旺盛，田孝华，侯志强，等.基于关键区域特征匹配的视觉跟踪算法［J］.电子学报.2014，42（11）：2150－2156.