视觉技术辅助的无人机自主着陆组合导航研究

蔡 鸣，孙秀霞，徐 嵩，刘 希，刘 日

（空军工程大学 航空航天工程学院，陕西 西安710038）

引言

自主着陆是影响无人机能否安全回收从而重复使用的重要因素之一［1］。在着陆过程中，导航系统发挥着至关重要的作用，但目前广泛使用的惯性导航系统（inertial navigation system，INS）会产生随时间积累的误差，全球定位系统（global position system，GPS）在战时的实用性受到限制，因此须将不同导航系统有机结合构成组合导航系统，扬长避短［2］。随着计算机视觉技术的飞速发展，其在无人机领域内的应用与日俱增，如运动目标检测［3］与空中加油的锥套跟踪［4］，与此同时，基于视觉（vision）的导航方法逐渐成为该领域内的研究热点。由于视觉导航方法不需要接受外界信号，以之取代GPS与INS构成组合导航系统，可以大大增加导航系统的自主性［5－6］，目前主要应用于自主着陆［7］、长僚机配合［8］等相对导航中。

文献［9］研究了无人直升机自主着舰中基于视觉图像处理的运动状态估计问题，利用色标在图像中的线、点等几何信息作为求解依据；文献［10］设计了一种仅依靠视觉传感器数据的无人机俯仰角与高度估计方法，并利用自适应卡尔曼滤波提高高度参数的估计精度。但以上文献中都用到了人工预置的辅助着陆图像，在缺少无人着陆场景信息的情况下适应性受到限制。

射影几何理论中，多视图几何作为一个重要理论被广泛研究，旨在利用同一特征在多个投影图像之间的对应关系解决视觉问题。在利用图像处理技术成功实现各幅图像之间特征匹配的前提下，多视图几何与辅助特征形状无关［11］。本文基于单目摄像机两个时刻所拍摄地面图像之间的双视图几何关系，设计了Vision／INS组合导航方法，有效地减少了对辅助着陆特征的要求，在能够任意实现前后时刻图像特征匹配的场景中均可适用。

Vision／INS组合导航系统中，常用的滤波算法包括扩展卡尔曼滤波（extended kalman filter，EKF）和无迹卡尔曼滤波（unscented kalman filter，UKF），但分别由于近似误差较大与计算效率低等原因导致滤波性能降低甚至失效。作为一种UKF方法的改进形式，本文采用平方根无迹卡尔曼滤波（SR－UKF），有效地避免以上缺点，为组合导航提供了更高效、准确的滤波技术。

1 Vision／INS信息融合方案

本文所设计的Vision／INS信息融合方案如图1所示。

图1 Vision／INS组合导航方案Fig.1 Integrated navigation scheme for Vision／INS

2 滤波模型

2.1 坐标系选取

在本文中选取东－北－天坐标系为导航坐标系，机体坐标系为前右下方向。为简便解算过程，假设摄像机坐标原点与机体坐标系原点重合。对于摄像机而言，采用针孔模型描述投影关系，如图2所示。

图2 摄像机针孔模型Fig.2 Pinhole camera model

图2中Ocxcyczc为摄像机坐标系，Ouxuyu为图像像素坐标系，［u0v0］为光心Oc在图像平面上的投影，称为主点，Pn＝［xn，yn，zn，1］T为导航坐标系中某点的齐次坐标，其图像平面上的对应投影点的齐次坐标为Pu＝［u，v，1］T。两者之间的射影关系可以表示为

式中：s为比例因子；Kcam为摄像机内参数矩阵；［R T］为摄像机的外参数矩阵；R和T＝－R˜C分别为摄像机坐标系到导航的旋转矩阵和平移向量；˜C为光心Oc的非齐次坐标。

2.2 过程方程

将INS误差与惯性元器件漂移作为滤波器的状态量，表示为X＝［ΔPosTΔVTΔΨTΔT

εT］，其中ΔP∈R3、ΔV∈R3和ΔΨ∈SO（3）分别表示位置误差、速度误差和姿态误差，ε∈R3和Δ∈R3分别表示陀螺漂移和加计零偏。由文献［12］可知，连续系统的过程方程为

其中，

式中：［fn×］表示由fn＝fb构成的反对称矩阵；为机体系到导航系的方向余弦阵；fb为比力；eV和eΨ表示速度和姿态角的测量高斯白噪声。考虑离散模型，对（2）式进行一阶近似离散化可得：

其中，

2.3 基于双视图几何的量测方程

选取感兴趣特征在图像坐标系上投影点的像素坐标作为滤波器的观测量，基于双视图几何关系构建量测方程。

若tk－1时刻的摄像机系相对于导航系的旋转矩阵和平移向量分别为 Rtk－1＝I3×3、Ttk－1＝03×1（即将其视为导航系）、诱导平面π上某一世界特征点Pn在图像平面上投影点齐次坐标，tk时刻摄像机系相对于导航系的旋转矩阵和平移向量分别为Rtk，tk－1和Ttk，tk－1，则tk时刻图像平面中对应投影点的齐次坐标可以表示为

其中 Htk，tk－1称为单应矩阵，且

式中：n为诱导平面π的单位法向量；d为诱导平面到tk－1时刻摄像机坐标系原点的距离［13］。

从定义中可以看出，双视图几何中所有量都定义在前一时刻的摄像机坐标系下，不适用于导航问题。若将（6）式表达的双视图间的单应矩阵约束作为量测方程的基础，应用到Vision／INS组合导航系统中，必须将在导航坐标系中描述的参数转换到tk－1时刻的摄像机坐标系下，实行一次坐标变换。

若tk－1时刻某个时变参数在导航系中的非齐次坐标为，则通过坐标变换将其转换到tk－1时刻的摄像机系（用表示）后，有

式中：Rtk－1＝Eulr2DCM（Ψtk－1）为tk－1时刻导航系到摄像机系的方向余弦阵（Eulr2DCM表示将欧拉角转换为方向余弦阵的函数）；为tk－1时刻摄像机光心在导航系中的非齐次坐标，当机体系与摄像机系重合时，有＝Postk－1。

为了使单应矩阵适用于组合导航，需要对以下矢量进行代换。

1）在tk－1时刻摄像机系中摄像机的平移向量的

由于平移向量与光心位置的关系为

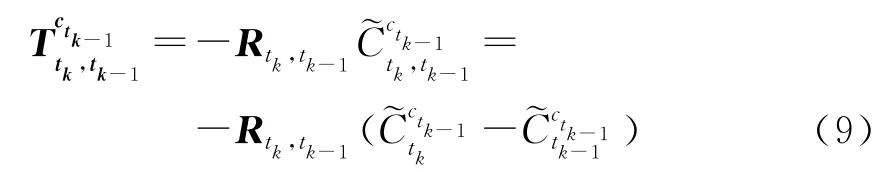
其中

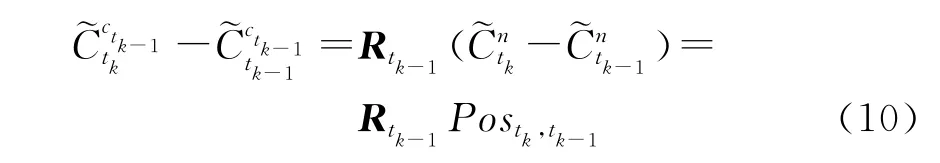
则

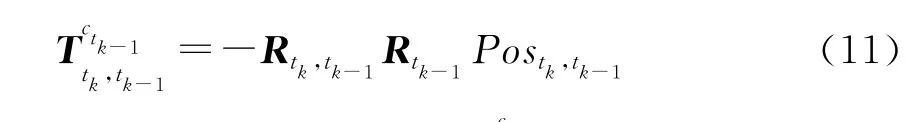
首先将导航系原点坐标On＝［0 0 0］T变换到tk－1时刻的摄像机系中，有

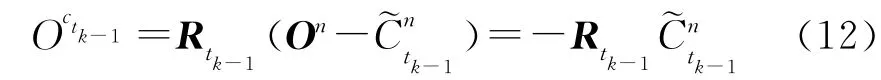
由于特征点所在平面为导航系坐标系的Onxnyn平面，所以诱导平面的法向量在导航系中的坐标为nn＝［0 0 1］T，则其在tk－1时刻的摄像机系中的坐标为

经过上面的坐标变换，将（11）式和（13）式带入（7）式中，单应矩阵可改写为

将其与不同时刻的导航参数通过以下形式相联系：

所以（7）式最终可表示为

综合所得，由双视图几何中单应矩阵关系决定的量测方程为

式中：函数H（·）表示由（16）式和（17）式构成的非线性运算；Vk∈R2为图像量测的高斯白噪声。

3 基于SR－UKF的算法实现

传统UKF算法中，在利用前一周期的状态估计值与误差方差矩阵获取Sigma点集时，需要对误差方差阵进行开方，若方差矩阵的阶数过高，采样过程会增加计算机的计算负担，降低运行效率。另外，由于计算机在数值运算过程中存在舍入操作，可能使误差方程矩阵非正定，导致开方运算失败以致滤波失效。因此，Rudolph［14］提出了SRUKF，在不改变运算复杂度的前提下提高了UKF的运算效率，并且避免了误差方差矩阵出现非正定的情况。

SR－UKF的主要思想是利用误差方差阵的Cholesky分解矩阵代替其自身参加滤波算法的迭代更新，避免每次Sigma点采样时的矩阵开方。在滤波算法的迭代更新过程中，主要用到的3个数学工具分别为矩阵的QR分解、Cholesky因子更新以及有效最小二乘法。应用于本文的滤波器模型，具体算法流程如图3所示。

图3 组合导航滤波算法流程图Fig.3 Flow chart of integrated navigation filtering algorithm

1）初始化

令初始时刻的INS参数误差与协方差矩阵的Cholesky分解因子为

同时，定义SR－UKF中所用的权值式中：λ＝α2（n＋k）－n；α决定点集中的采样点到均值的距离，通常赋予较小正值（10－4≤α≤1）；k≥0用于保证方差阵的半正定性；β≥0用于包含状态量分布的高阶成分。

2）Sigma点计算与时间更新

Sigma点计算与时间更新公式为

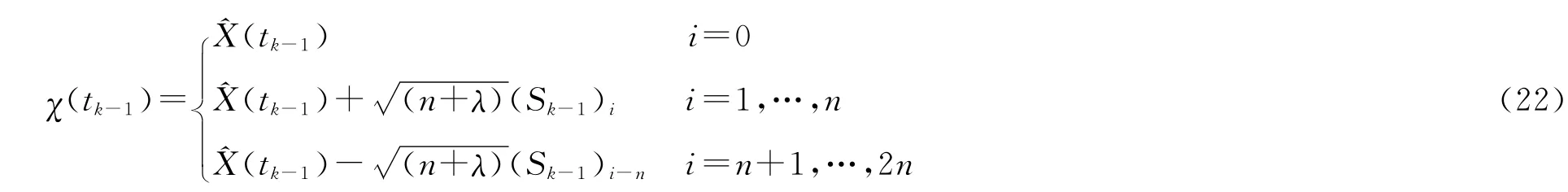
其中（Sk－1）i为矩阵Sk－1的第i列，即：

式中：矩阵Q表示系统过程噪声Wk的方差阵；qr（·）返回矩阵QR分解所得R阵中的上三角矩阵；cholupdate（·）表示Cholesky一阶更新。因此有：

其中R表示量测噪声Vk的方差阵。因此有

3）量测更新

量测更新公式为

4 仿真结果与分析

在Matlab仿真环境中，首先利用轨迹发生器生成无人机着陆运动轨迹，如图4所示。

图4 无人机着陆轨迹与跑道特征点标识Fig.4 UAV landing trajectory and track feature points identification

无人机从偏离跑道中心线45°方向进入对准阶段，其初始位置为Pos（t0）＝［－51.65 505 42.63］Tm，初始速度为V（t0）＝［7 －7 0］Tm／s，经过9s后对准跑道中心线，并继续匀速飞行5s准备进入下滑阶段。图4中起点A与终点B之间的轨迹为无人机的着陆轨迹，地面两条平行线为跑道边缘，周围对称分布9×11个地面特征点。基于着陆轨迹，可以计算理想的导航参数变化曲线，如图5所示。

图5 无人机着陆理想导航参数Fig.5 UAV landing ideal navigation parameters

将加计零偏和陀螺漂移视为常值偏差，其设定如表1所示。

表1 惯性测量单元常值漂移Table 1 Constant drift of inertial measurement unit

将加计零偏、陀螺漂移和图4所示的理想加速度与角速度（欧拉角的微分）相加，从而模拟加速度计与陀螺在实际工作中的输出值利用捷联惯导算法解算得到INS位置、速度、姿态角误差，分别如图5（a）、5（b）、5（c）中的虚线所示。

在Vision／INS组合导航仿真实验中，设定滤波器状态初始值为

其中，

初始状态的协方差阵为

令W 与V均为高斯白噪声，其方差阵分别为

选择INS解算周期为0.1s，SR－UKF的滤波周期为1s，即INS每解算10次进行1次校正；进行100次蒙特卡洛仿真后，得到组合导航的参数误差曲线如图6中实线所示。

图6 组合导航与惯导误差对比Fig.6 Navigation and inertial navigation error comparison

从误差曲线对比图中可以看出：

1）本文设计的基于双视图几何的Vision／INS组合导航系统输出的经过校正的位置和速度参数的误差明显减小，精度有了很大程度的提高，其误差最大值与在同一时刻INS误差的比较列写于表2。

表2 位置与速度误差比较Table 2 Position and velocity error comparison

2）导航参数误差保持在一定的平稳水平，体现了本文所设计的INS／Vision组合导航可以有效地抑制INS误差随时间积累导致的发散。

3）对于姿态角而言，滚转角与俯仰角误差精度提高较为明显，而偏航角误差与INS基本保持在同一水平。

将理想着陆轨迹、INS单独工作时的导航轨迹、本文的组合导航轨迹比较列于图7中。从图7可以看出，与INS相比，组合导航获得的轨迹与真实轨迹十分接近。

最后，为了验证本文中所使用的双视图几何约束，选取第34s这一时刻，将利用特征点世界坐标与理想轨迹计算所得的理想图像点，以及利用第33s的图像点与双视图几何滤波器所估计的观测图像点在图8中进行了比较。从图8中可以看出，利用双视图几何滤波器计算得到的图像点与真实图像点相差不多，体现了算法的正确性。

图7 3种着陆轨迹的对比Fig.7 Contrast of three landing trajectories

图8 真实图像点与双视图几何滤波器估计图像点对比Fig.8 Contrast of true image points and two－view geometry filter estimated image points

5 结论

本文以无人机自主着陆为工程背景，设计了一种Vision／INS组合导航方案。针对地面特征须人工预置的条件约束，基于双视图几何设计了滤波器，并利用SR－UKF估计INS误差，有效地实现视觉信息与惯性信息的融合。与INS相比，组合导航系统的参数精度显著提高，且具有良好的自主性。

［1］ Zhang Jianhong，Zhang Ping.Autonomous precise landing control law for UAV［J］.Journal of System Simulation，2009，21（3）：743－748.张建宏，张平.无人机自主精确着陆控制律设计及仿真研究［J］.系统仿真学报，2009，21（3）：743－748.

［2］ Liu Jianye，Zeng Qinghua，Zhao Wei，et al.Navigation system theory and application［M］.Xi'an：Northwestern Polytechnical University Press，2010.刘建业，曾庆化，赵伟，等.导航系统理论与应用［M］.西安：西北工业大学出版社，2010.

［3］ Dong Jing，Fu Dan，Yang Xia.Real－time moving object detection and tracking by using UAV videos［J］.Journal of Applied Optics，2013，34（2）：255－259.董晶，傅丹，杨夏.无人机视频运动目标实时检测及跟踪［J］.应用光学，2013，34（2）：255－259.

［4］ Wang Xufeng，Dong Xinmin，Kong Xingwei，et al.MS－KF fusion algorithm for drogue tracking［J］.Journal of Applied Optics，2013，34（6）：951－956.王旭峰，董新民，孔星炜，等.MS－KF融合算法用于锥套跟踪［J］.应用光学，2013，34（6）：951－956.

［5］ Roumeliotis S，Johnson A，Montgomery J.Augmenting inertial navigation with image－based motion estimation［J］.IEEE International Conference on Robotics and Automation，2002，4：4326－4333.

［6］ Li Jian，Li Xiaomin，Qian Kechang，et al.Motion state estimation for micro UAV using inertial sensor and stereo camera pairs［J］.Acta Aeronautica et Astronautica Sinica，2011，32（12）：2310－2317.李建，李小民，钱克昌，等.基于双目视觉和惯性器件的微小型无人机运动状态估计方法［J］.航空学报，2011，32（12）：2310－2317.

［7］ Gao Yangjun，Sun Xiuxia，Liu Yukun，et al.A hybrid iterative quasi－sliding mode control strategy for autolanding of UAV［J］.Flight Dynamics，2013，31（6）：521－525.高杨军，孙秀霞，刘宇坤，等.无人机自主着陆的双环混合迭代滑模控制［J］.飞行力学，2013，31（6）：521－525.

［8］ Wang Xiaogang，Guo Jifeng，Cui Naigang.A relative navigation method based on INS／Vision for UAV［J］.Journal of Harbin Institute of Technology，2010，42（7）：1029－1032.王小刚，郭继峰，崔乃刚.INS／Vision相对导航系统在无人机上的应用［J］.哈尔滨工业大学学报，2010，42（7）：1029－1032.

［9］ Qiu Liwei，Song Zishan，Shen Weiqun.Computer vision scheme used for the automate landing of unmanned helicopter on ship deck［J］.Acta Aeronautica et Astronautica Sinica，2003，24（4）：331－335.邱力为，宋子善，沈为群.用于无人直升机着舰控制的计算机视觉技术研究［J］.航空学报，2003，24（4）：331－335.

［10］Pan Xiang，Ma Deqiang，Wu Yijun，et al.Estimating pitch attitude and altitude of unmanned aerial vehicle vision－based landing［J］.Journal of Zhejiang U－niversity：Engineering Science，2009，43（4）：1029－1032.潘翔，马德强，吴贻军，等.基于视觉着陆的无人机俯仰角与高度估计［J］.浙江大学学报：工学版，2009，43（4）：1029－1032.

［11］Hartley R.Multiple view geometry in computer vision［M］.London：Cambridge University Press，2003.

［12］Indelman V，Gurfil P，Rivlin E.Real－time mosaic－aided aerial navigation：II.sensor fusion［C］／／AIAA modeling and simulation technologies conference，2009.Reston，VA：AIAA，2009.

［13］Wu Fuchao.Mathematical technique of computer vision［M］.Beijing：Science Press，2008：89－91.吴福朝.计算机视觉中的数学方法［M］.北京：科学出版社，2008：88－91.

［14］Der Merwe R A，Wan E A.The square－root unscented kalman filter for state and parameter estimation［C］／／Proceedings of IEEE international conference on acoustics，speech and signal，Salt Lake City，Utah，USA，2001.USA：IEEE，2001：3461－3464.