三轴光电侦查平台可周转指向光束姿态算法设计

尹 剑，高教波，张琬琳，陈 红

（西安应用光学研究所，陕西 西安710065）

概述

某三轴可旋转光电侦查载体平台在工作时，发射一束指向光束，该光束可以在载体平台平面上进行全周转动，旋转的角度可以测得。光电平台在进行后续定位计算及图像处理时，需要知道该光速的姿态角，即该光束的坐标在地理坐标系下的方位轴转过角度和俯仰轴旋转的角度。

这个问题可以用坐标系加以描述，如图1所示，地理坐标系（g系）采用东、北、天坐标系标记为E、N、D；载体坐标系（b系）标记为X、Y、Z，其中，Y沿机体纵向轴向前，X沿机体横轴指向右，Z与X、Y构成右手定则沿机体垂直向上；光束坐标系（u系）标记为X1、Y1、Z，其中光束坐标系的Z轴与载体坐标系的Z轴为同一个轴，且光束坐标系只围绕Z轴在载体X、Y轴平面的旋转。如图1所示，α角即为光束坐标系绕Z轴转过的角度。

图1 坐标示意图Fig.1 Coordinates system

图2对实体平台进行坐标系抽象，其中ψ、θ、γ分别为载体平台坐标系航向角、俯仰角和横滚角，也就是载体坐标系相对于地理坐标系3个轴旋转的角度；Ψ1、θ1就是光束的坐标系相对于地理坐标系的两轴旋转角度，分别为航向角、俯仰角即光束的姿态角。

图2 旋转角度示意Fig.2 Diagram of circumrotation angle

1 采用四元数法算法

1.1 算法描述

四元数是一个由4个元构成的数，其形式为

在刚体定点转动理论中，根据欧拉定理，动坐标系相对参考坐标系的方位，等效于动坐标系绕某一个等效转轴转动一个角度θ。如果用u表示等效转轴方向的单位向量，则动坐标系的方位完全由u和θ两个参数确定。用u和θ可构造一个四元数如转动后的矢量用r′表示，则以四元数描述的r′和r的坐标变换关系为，其中

根据这个性质，可用四元数表示地理坐标系到光束坐标系的变换关系：

设载体平台四元数为

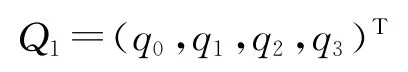
根据四元数性质，由于光束绕Z轴旋转角度为α，可知旋转四元数为Q2＝（p0，p1，p2，p3）T，式中：p0cos（α／2）；p1＝0；p2＝0；p3＝－sin（α／2）。

于是，旋转后的四元数为

Q3＝（r0，r1，r2，r3）T

其中Q3＝Q1⊗Q2，展开成矩阵形式为

则Q3就是光束的四元数，利用（1）式，根据这个四元数求得光束坐标姿态矩阵，然后利用这个姿态矩阵进行姿态角转换如下，

就可以求出光束坐标系的姿态值。其中，（1）式和（2）式见文献［1］。

1.2 算法仿真

利用四元数算法，模拟平台水平和侧倾90°两种情况时光束坐标绕Z轴从0°到360°进行旋转，计算结果与预期值一致。

当光电平台水平时，光束坐标Z轴从0°到360°进行旋转，四元数算法求得光束的姿态值，如图3所示。

当光电平台横滚90°时，光束坐标Z轴从0°到360°进行旋转，用四元数算法求得光束的姿态值，如图4所示。

图3 平台水平时四元数算法光束姿态仿真Fig.3 Quaternion algorithm simulation for horizontal platform

图4 平台侧倾90度时四元数算法光束姿态仿真Fig.4 Quaternion algorithm simulation for vertical platform

2 采用坐标变换算法

2.1 算法描述

根据上述该问题的坐标变换描述，地理坐标系（g系）绕负D转ψ角，绕E轴转θ角，再绕N轴转γ角，得到光电平台机体坐标系（b系），利用坐标变换算法，其姿态矩阵为

在平台坐标系（b系）的基础上，光束坐标系绕Z轴继续旋转角度为α，得到光束坐标系（u系），变换算法如下：

其中，

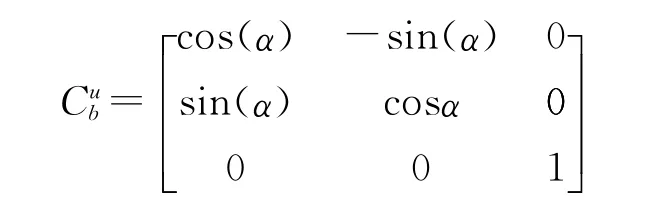
则有：

根据（2）式就可以得到光束姿态值如下：

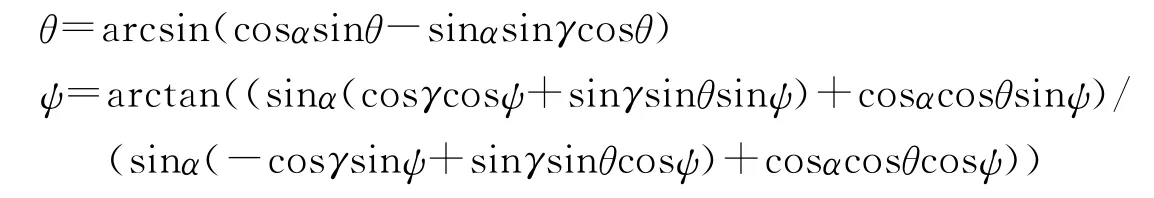
2.2 算法仿真

利用坐标变换算法，模拟平台水平和侧倾90°两种情况时光束坐标绕Z轴从0°到360°进行旋转，当光电平台水平时，光束坐标Z轴从0°到360°进行旋转，用坐标变换算法求得光束的姿态值，如图5所示。

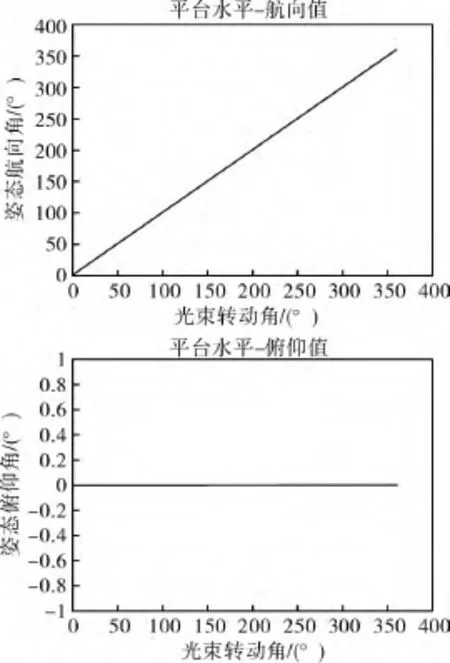
图5 平台水平时坐标变换算法光束姿态仿真Fig.5 Coordinate transformation algorithm simulation for horizontal platform

图6 平台侧倾90°时坐标变换算法光束姿态仿真Fig.6 Coordinate transformation algorithm simulation for vertical platform

当光电平台横滚90°时，光束坐标Z轴从0°到360°进行旋转，用坐标变换算法求得光束的姿态值，如图6所示。

3 结论

针对某三轴可旋转光电侦查平台上光束旋转的姿态计算问题，分别采用了四元数算法和坐标变换算法进行了推算。经过仿真验证，这两种算法都能够得到正确结果。相比较而言，坐标变换算法形式简单，便于理解和实现。但是，坐标变换算计算过程中大量使用三角函数计算，而三角函数计算在工程实现时采用级数展开的方式，展开的级数的多少因计算机及处理器的不同而有差异，因此计算量大，实时性差；而四元数算法使用的三角函数计算很少，从而更易于工程应用。

［1］ Qing Yongyuan.Stapdown inertial navigation［M］.Xi'an：Northwestern Polytechnial University Press，2006.秦永元.惯性导航［M］.西安：西北工业大学出版社，2006.

［2］ Yang Peigeng，Gong Zhibing.Photoelectricity inertial technology ［M］.Beijing：Ordnance Industry Press.1999：195－199.杨培根，龚智炳.光电惯性技术［M］.北京：兵器工业出版社，1999：195－199.

［3］ Deng Zhenglong.Inertial technology［M］.Harbin：Harbin Institute of Technology Press， 2006：140－180.邓正隆.惯性技术［M］.哈尔滨：哈尔滨工业大学出版社，2006：140－180.

［4］ Hu Xiaoping.Self navigation theory and application［M］.Changsha：National University of Defense Technology Press，2002.胡小平.自主导航理论与应用［M］.长沙：国防科技大学出版社，2002.

［5］ Jin Yimin，Tao Zhong，Sun Zhijia.Mathematical simulation and shafting errors of shafting movement ［J］.Journal of Applied Optics，2003，24（S）：37－46.金毅民，陶忠，孙治家.轴系运动的数学仿真与轴系误差 ［J］.应用光学，2003，24（S）：37－49.

［6］ Zhang Ronghui，Jia Hongguang，Chen Tao，et al.Attitude solution for strapdown inertial navigation system based on quaternion algorithm ［J］.Optics and Precision Engineering，2008，16（10）：1964－1970.张荣辉，贾宏光，陈涛，等.基于四元数法的捷联式惯性导航系统的姿态解算［J］.光学精密工程，2008，16（10）：1964－1970.

［7］ Li Xiaoguang，Wang Zhaonan，Wang Zhi，et al.Research on location compute method of object［J］.Optics and Precision Engineering，2006，14（6）：1076－1081.李晓光，王兆楠，王智，等.一种目标位置解算方法［J］.光学精密工程，2006，14（6）：1076－1081.

［8］ Zhang Wanlin，Yin Jian，Guo Shuanyun.Temperature compensation for Q－MEMS gyro［J］.Journal of Applied Optics，2010，31（4）：549－552.张琬琳，尹剑，郭栓运，Q－MEMS陀螺零偏补偿技术研究［J］.应用光学，2010，31（4）：549－552.

［9］ Liu Junfeng.Three dimensional rotation represented by quaternion［J］.College Physics，2004，23（4）：39－43.刘俊峰.三维转动的四元数表述［J］.大学物理，2004，23（4）：39－43.

［10］Liu Haiying，Wang Huinan，Liu Xinwen.Attitude measurementising quaternion based on UKF［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2006，38（1）：37－42.刘海颖，王惠南，刘新文.基于UKF的四元数载体姿态确定［J］.南京航空航天大学学报，2006，38（1）：37－42.

［11］Yang Yanjuan.Study on the crucial technology of SINS［D］.Harbin：Harbin Engineering University，2001.杨艳娟.捷联惯性导航系统关键技术研究［D］.哈尔滨：哈尔滨工程大学，2001.