三维形貌测量激光雷达光学系统设计

张欣婷，亢 磊，安志勇

（1.长春理工大学 光电信息学院，吉林 长春130012；2.中国北车长春轨道客车股份有限公司，吉林 长春130083；3.长春理工大学，吉林 长春130022）

引言

近些年来轨道交通业的不断发展，对人们的出行带来了极大的方便，尤其是北车集团长春轨道客车股份有限公司研制的CRH380高速动车组出现后，大大提高了运行速度、缩短了旅途中所占用的时间，这也是动车组大受欢迎的原因之一。但是，由于列车在高速行驶的过程中所受的阻力过大，难免会引起车头的变形。尽管CRH380的车头形状已经在低速动车组的基础上加以改进，设计成了子弹头型，以减小阻力，但是出于安全考虑，仍然需要经常对其三维形貌进行检测，而且不仅需要在列车出厂前对其面型进行检测，在使用和运行过程中也同样需要进行检测。针对上述需求，在现有三维形貌测量的基础上，研制出了一款基于激光雷达原理的、用于大尺寸三维形貌测量的系统。本文主要对其光学系统和与光学系统有关的相应技术展开研究。

在大尺寸物体的三维形貌测量领域，快速获取高精度的测量数据己经成为一个重要研究方向，其中有很多关键性技术问题有待解决。目前国内在这一领域主要是应用三坐标测量机，但三坐标测量机只能针对一些中小尺寸的产品进行测量，且对环境要求较高，通常在室内恒温条件下测量。而大尺寸的测量多数是在室外，甚至是在野外恶劣条件下进行，三坐标测量机则无法满足其要求。因此，现在更多使用的是国外的进口仪器，主要是英国雷尼绍公司、德国GOM公司、日本罗兰公司和英国泰勒霍普森有限公司的相关产品。国内天津大学叶声华教授所在的精密测试技术及仪器国家重点实验室也对激光雷达做了深入研究并取得了显著成果。但国内产品无论是测量精度、效率、实时性，还是数据处理等，都与国外产品存在着较大的差距。

本设计主要是针对上述问题，利用激光差频干涉原理，采用基于迈克尔逊干涉仪的光路结构，设计了一种新型三维面型激光测量系统。该系统实现测距的同时，再根据轴角编码器给出的距离和水平角、俯仰角，通过球形坐标系和笛卡尔坐标系的转换得出被测点的（X，Y，Z）坐标。本文主要介绍激光测距部分的发射／接收光学系统设计［1］，并给出最终的实验测量数据。

1 发射光学系统设计

由于该激光雷达要求能测量2m～18m范围内的三维面型，测量精度达到0.02mm／m，因此在激光发射系统中，为了增大作用距离，就要提高发射系统的准直性。若要达到此目的，需要加准直扩束系统来减小激光器出射光的发散角，扩束比越高，发射系统的准直性也越高。当出射光束腰在焦平面上时，该发射系统可达到最大扩束比。本系统采用3个倒置的伽利略望远镜构成3次扩束准直，再通过对前组物镜的微小移动进行离焦，使系统在2m～18m范围内均能在目标上形成能量最集中、尺寸最小的光斑，以保证获得最大的回波能量进入接收系统。

1.1 高斯光束参数的确定

高斯光束经单薄透镜成像公式和物像比例公式［2－3］

式中：z0为瑞利长度，且

若激光器的激光管腔长为l，两反射镜半径分别为R1和R2（出射面半径），由激光光学可知

束腰距出射面的距离为

当薄透镜焦距f一定时，将（2）式对s0求一阶偏导数，得到

由（6）式可以得出结论，当s0＞f时，ω0随s0的减小而单调增加；当s0＜f时，ω1随s0的增大而单调增加；当s0＝f时，ω1达到极大值，由（2）式可求出

将s0＝f代入（1）式，得s1＝f。

另外，远场发散角θ0与准直扩束后的激光的距离z′处的光斑直径D有：

可见，将高斯光束中入射光束和出射光束的束腰比作为几何光学中近轴光线的聚焦点，高斯光束经透镜变换后的聚焦特性与普通几何光学中近轴光线的聚焦特性的差异是很大的。当入射高斯光束的束腰位于透镜左方焦点附近时，出射高斯光束的束腰并不在无穷远，而是位于透镜右方焦点附近。ωi达到极大值时，远场发散角θ0达到极小值，是理想的准直扩束条件。

由上述公式的约束条件，最终确定发射光学系统的入瞳直径为8mm，经过扩束准直后的透镜口径为60mm，旋转反射镜口径为60mm。

1.2 设计结果

发射光学系统只采用两种普通光学玻璃BK7和SF8共9片透镜，设计成无焦系统。利用Zemax软件［4］当中的多重结构来移动第一片负透镜，对系统进行微小的离焦，第一片透镜和第二片透镜之间的距离在28.203mm～14.671mm之间变化时，系统在2m～18m的范围内均能汇聚成能量集中的光斑。发射系统光路如图1所示，使用了3次扩束准直，达到了8倍的扩束比。中间的分束镜可将回波光束沿垂直方向反射，实现发射、接收共光路。

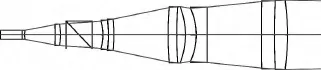
图1 发射光学系统Fig.1 Launching optical system

图2所示为作用距离为18m时发射系统的点列图，图2中显示艾里斑为568.4μm（小于18 m的测量范围内，艾里斑均小于该值，本文不再一一给出图形），经计算，满足该三维形貌测量的精度要求。

图2 点列图Fig.2 Spot diagram

图3为作用距离为18m时发射系统的波像差图，图中显示其峰谷值为0.049 7λ，满足瑞利判据所要求的小于0.25λ的要求。

图3 波像差Fig.3 Wave aberration

1.3 变倍曲线

利用Zemax软件中的宏语言ZPL进行编程，并对该发射系统的无焦变倍曲线进行仿真，在2m～18m范围内，给出系统第一片负透镜连续变动与其焦距的变化曲线，其结果如图4所示。横坐标为测量距离，纵坐标为系统焦距。当发射系统焦距在28.203mm～14.671mm之间变化时，可实现测量距离2m～18m。

图4 发射系统变倍曲线Fig.4 Launching system zoom curve

从图4中可以看出，该发射系统的变倍曲线较为平滑，可以实现平稳的连续变倍，即在2m～18m之间的任意距离，均能获得能量最集中的光斑。

2 接收光学系统设计

接收系统设计成与发射系统共光路的形式，共用棱镜后面的部分，棱镜前采用耦合透镜将由目标返回的光线耦合进光纤。

2.1 激光雷达测距方程

激光雷达的测距方程会因为探测目标的不同而具有特殊的变化，其探测目标主要为点目标、扩展目标和线性目标［5－6］。

当接收到的是被测目标的全部反射光束时，可以认为该目标是扩展目标。本系统的被测距离为2m～18m，对于激光雷达来说属于近距离测量，因此大气影响可近似考虑为单程传输影响，通常也被看做是扩展目标。此时使用激光雷达的另一种表示形式：

式中：Pt为激光器发射光功率；Pr为探测器接收光功率；σ为目标的散射截面；D为目标口径；ηA为大气传输系数（接收光学系统的透过率）；ηO为光学系统传输系数（发射光学系统的透过率）。

针对扩展目标，由朗伯散射，得：

式中：θ为激光器发射光的衍射角；ρ为平均反射系数（目标反射率）。

将（11）式代入（12）式，有：

因为

将（13）式和（14）式代入（10）式，有：

本文利用雷达方程对系统的回波能量进行计算。因为该系统是用来测量大尺寸三维形貌的，本设计最终进行的实验是针对动车组子弹形车头面型的，因此这里选取相关参数时以子弹形车头为准。

首先，动车组在进行面型检测这一步骤时，车体表面是铝合金，而并未喷漆。通过查找材料手册，铝合金这种材质的反射率为73%～87%，镜面铝材质的反射率甚至高达95%，我们保守地取80%。其次，选取接收口径的大小。理论上，接收口径越大，所接收的回波能量越多，但通过实验发现，当接收口径达到某个最佳值之后，信噪比就会开始下降，也就是说接收口径不能过大。一般远距离传输的激光雷达，在选择接收口径时，要求略大于横向相干距离的2倍，根据经验，在85mm～100mm左右。本设计属于近距离测量，能量损失会相对减小，因此这里选取60mm为接收口径的尺寸。既保证了足够的回波能量，又不至于使系统体积过大。再次，反射目标的半径取1m，这也是个比较保守的数值，对于大尺寸测量来讲已经足够。最后，给出激光器发射功率Pt＝5mW；发射光学系统的透过率ηt＝90%，接收光学系统的透过率ηr＝90%。将以上条件代入（15）式，可得回波功率为

从计算结果可以看出，该回波功率是在μW量级，而接收该功率的探测器选取的是PIN光电二极管，它具有极高的响应力和灵敏度，完全可以探测到该回波信号，说明该设计比较合理。

2.2 设计结果

本设计选用的光纤数值孔径NA＝0.125。图5所示为接收系统光路，通过分束镜实现了前面所述的发射、接收共光路。

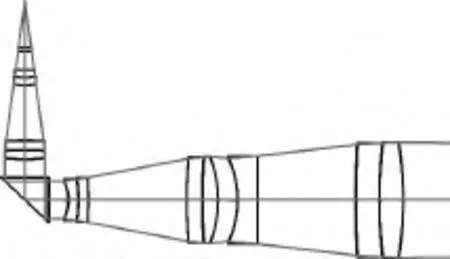
图5 接收光学系统Fig.5 Receiving optical system

图6所示为接收系统点列图，图中显示艾里斑为568.4μm，3个视场的的均方根半径均远小于艾里斑。

图6 点列图Fig.6 Spot diagram

图7为接收系统波像差图，图中显示其峰谷值为0.041 5λ，满足瑞利判据所要求的小于0.25λ的要求。

图7 波像差Fig.7 Wave aberration

3 实验结果

为了实现三维形貌测量，实验时在空间上同时选取多个点进行同一组测量，标定每一个点的三维坐标值。本实验进行了两组测量：第一组选定空间上的5个点，分别标定为P1～P5，测得三维坐标（X，Y，Z）的具体数值，针对这5个点测量500次。第二组选定空间上的6个点，分别标定为J1～J6，同样测量500次。为了更准确地反映系统的测量精度，这5个点的位置尽量不要太集中。测量完成后，分别对这两组的测量进行重复性测量分析等相关计算，可实现测量精度0.1mm／m。由于篇幅有限，这里只列举两组的一次测量数据，如表1所示［10－11］。

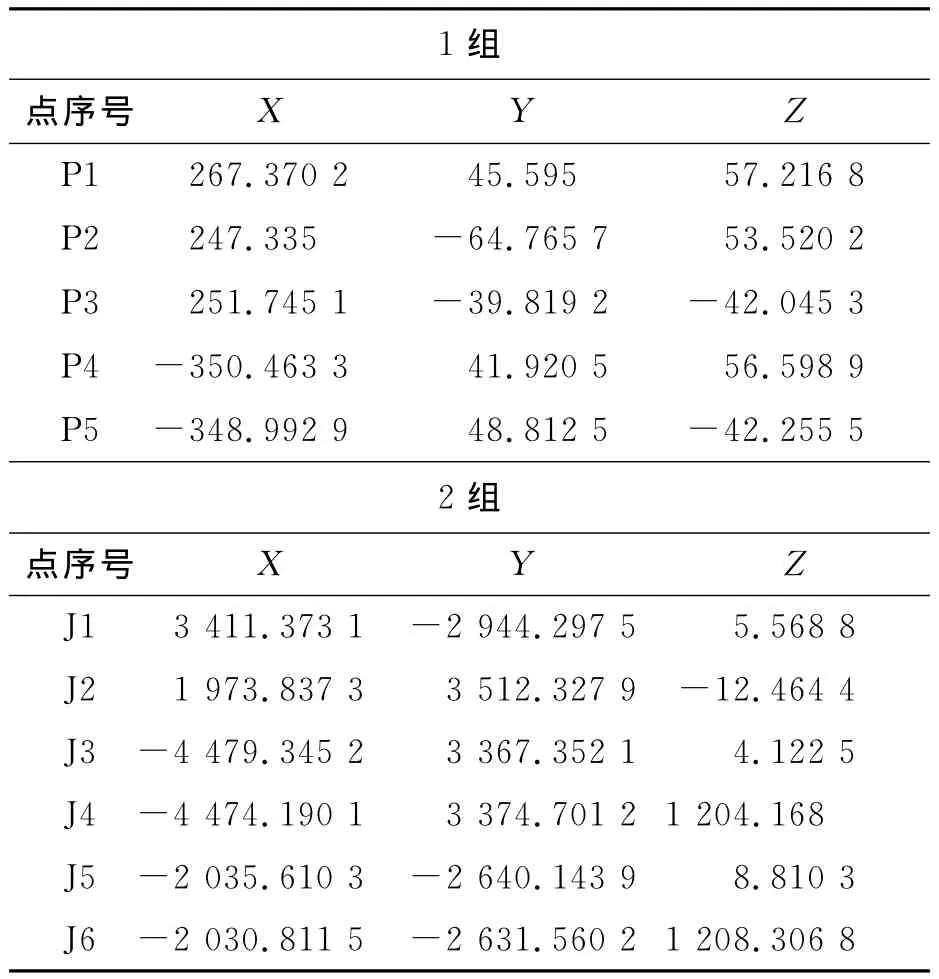
表1 三维坐标测量数据 mmTable 1 Three－dimensional coordinate measurement data

4 结论

本文设计了用于三维形貌测量的激光雷达发射／接收光学系统。发射系统根据高斯光束准直理论，确定光学系统的相关参数，设计了可用于2m～18m范围内的激光测距系统，同时利用Zemax的宏语言编程，绘制出变倍曲线。接收系统则根据激光雷达测距方程，确定目标的相关参数，以获取最大的回波能量，并通过光学系统将回波光束耦合进光纤。该系统的设计完成，可以解决长春轨道客车厂新型列车子弹型车头的面型检测及车体外形测量技术问题。这种光学三维形貌测量方法具有非接触、测量速度快、精度高、在计算机控制下实行自动化测量等优点，尤其对汽车产业、轨道客车等产业的发展具有重要意义。

［1］ Albert B.Laser radar systems［M］.Boston：Artech House，1992.

［2］ Xiao Zexin，Engineering optics design［M］.Beijing：Electronic Industry Press，2002.萧泽新.工程光学设计［M］.北京：电子工业出版社，2002.

［3］ Zhang Le.Study on emitting and receiving optical systems of lidar［D］.Changsha：National University of Defense Technology，2004.张乐.激光雷达发射和接收光学系统研究［D］.长沙：国防科学技术大学，2004.

［4］ The ZEMAX Chinese user manual［M］.Shanghai：The Infotek Optoelectronics Technology（Shanghai）Co.，Lt，2005.ZEMAX中文使用手册［M］.上海：讯技光电科技（上海）有限公司，2005.

［5］ Guo Yulan.Wan Jianwei，Lu Min，et al.Three dimensional laser radar target pose estimation［J］.Optics and Precision Engineering，2012（4）：843－850.郭裕兰，万建伟，鲁敏，等.激光雷达目标三维姿态估计［J］.光学精密工程，2012（4）：843－850.

［6］ Mei Zhiyu.Analysis of stray light of coherent laser radar optical system ［D］.Changchun：Changchun U－niversity of Science and Technology，2012.梅志宇.相干激光雷达光学系统杂散光分析［D］.长春理工大学.2012.

［7］ Tan Xuechun.Laser radar simulation device and experimental research［D］.Changchun：Changchun University of Science and Technology，2012.谭雪春.激光雷达模拟样机系统与实验研究［D］.长春：长春理工大学，2012.

［8］ Pan Hongtao.Research on ladar of irfrared laser dual－mode seeker ［D］，Harbin ：Harbin Institute of Technology.2009.潘洪涛.红外激光双模制导中激光雷达技术研究［D］.哈尔滨：哈尔滨工业大学，2009.

［9］ Qu Zengfeng，Jin Chenfei，Zhao Yun，et al.Theoretical analysis of structure and operation range calculation of a novel fiber lidar［J］.Infrared and Laser Engineering，2009，38（2）：300－303.屈增风，靳辰飞，赵远，等.新型光纤激光雷达的结构理论分析与作用距离计算［J］.红外与激光工程，2009，38（2）：300－303.

［10］Sun Guoqiang.Error analysis and correction of 3D radar［D］.Hefei：Hefei University of Technology，2012.孙国强.三坐标雷达误差分析与修正［D］.合肥：合肥工业大学，2012.

［11］Jiang Haijiao.Lai Jiancheng.Wang Chunyong，et al.Research on ranging property of laser radar and its range accuracy［J］.Chinese Journal of Lasers，2011，38（5）：0514001－1－0514001－7.姜海娇，来建成，王春勇，等.激光雷达的测距特性及其测 距 精 度 研 究 ［J］.中 国 激 光，2011，38（5）：0514001－1－0514001－7.