LC空间中极大极小不等式问题的相关研究
2015-05-26叶久龄
叶久龄
一、引言及预备知识
1.引言
关于KKM定理的研究是目前非线性问题研究的热点内容之一,目前常见的研究,有些是空间条件复杂化,有些是集合条件复杂化,但采用加强空间条件以减弱集合条件的研究尚属少见,作者利用该思想进行了相关研究.关于本文KKM定理的研究,学者Yang Z.,Pu Y.J.仅仅是在假设局部凸空间的前提下,对应紧凸集给出了相应的KKM定理,但对LC空间上对应H-紧、H-凸集的研究尚属少见.作者在LC空间上对应H-紧、H-凸集给出了相应的KKM定理,并在该KKM定理的基础上在LC空间上给出了相关的极大极小不等式应用,具有一定的理论意义.
2.预备知识
定义1.1[1]:若S中的恒等映像与常值映像同伦,则称S是可缩集.
注:拓扑向量空间中每个凸集都是可缩集.
定义1.2[1]:设E是Hausdorff拓扑空间,是E的非空可缩子集的某个族,A与A'是E中一切有限子集,若满足则称为H-空间.
定义1.3[2]:设D是H-空间中的一个非空子集.若,则称D是H-凸集;若A是可缩的,则称D是弱H-凸集;若且是紧、弱H-凸集合,则称D是H-紧集.
定义1.4[3]:设E是基γ的一致空间,且基γ具有满足下列条件的一致结构:
注:为了叙述方便,我们将l.c.-Hausdorff空间简称为LC空间.
定义1.5[2]:设F是一个集值映射,若对Y的任意闭(开)子集是闭(开)的,则称F:E→2Y上半连续(下半连续).若F即是上半连续又是下半连续,则称F连续.
定义1.6[4]:设X是LC空间 中的非空H-紧、H-凸子集.若对任意具有闭值的上半连续映射f:X→X都存在不动点,则称X具有不动点性质.
二、LC空间中的KKM定理
定义2.1[5]:设 是LC向量空间,X是E的非空H-紧、H-凸子集,F:X→E是一个集值映射,若对有限子集 ,存在一个连续函数: ,使得对任意λ∈△n,存在一个i∈J(λ)使得 ,则称F是广义KKM映射.
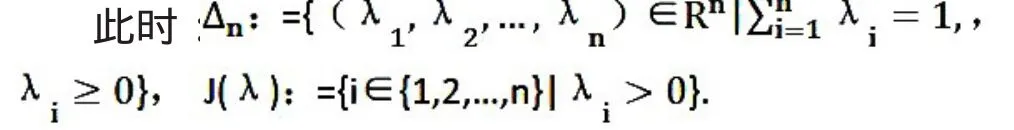
引理2.1[6]:设是LC空间,若是非空H-紧的,T:E→2D是上半连续集值映射且对每个x∈E,T(x)是闭H-凸集,则T有不动点.
注:因为连续集值映射显然是上半连续的,所以引理2.1对连续映射也成立.
三、常值形式的Ky Fan极大极小不等式
定义3.1[7][10]:设X是LC向量空间 中的一个非空H-紧、H-凸子集,若对任意有限子集 {y1,y2,…,yn} X,存在连续映射:,使得,存在 α∈(- ,+ ),α≥则称 f(x,y) 关于 y∈X是 α-拟凹的.此时 λ=(λ1,λ2, …λn)∈ ,J(λ):={i∈{1,2,…,n}|λi>0},:={(λ1,λ2,…λn)
定理3.1:设X是LC向量空间 中的一个非空H-紧、H-凸子集.若函数f:X×X→R∪{+ }满足:
(1)对于y∈X,f(x,y)关于x∈X是下半连续的;
(2)对于x∈X,f(x,y)关于y∈X是α-拟凹的;
则存在x*∈X使得对于任意y∈X,f(x*,y)≤α.
证明:若 α=+ ,结论显然成立.设- <α+ ,若集值映射F:X→2X满足:对于y∈X,F(y)={x∈X|(fx,y)≤α}.又由条件(1)可得,对于y∈X,(fx,y)关于x∈X是下半连续的,则F(y)在X中是闭的.由条件(2)可得,对于任意有限子集{y1,y2,…,yn} X,存在一个连续映射,使得∈,存在α≥mini∈J(λ)f((λ),y)i,此时 λ=(λ1,λ2,…λn)∈,J(λ):={i∈{1,2,…,n}|λi>0}.则 ,使得 α≥mini∈J(λ)f((λ),y)i=f((λ),yi0).由F的定义可得 (λ)∈F(yi0),则F是广义KKM映射.再由定理2.1可知,.若令 ,则存在x*∈X使得对于任意y∈X,(fx*,y)≤α.
四、函数形式的Ky Fan极大极小不等式
定义 4.1[8]:设是一个 LC 空间,B E,YE.若对于任意B的有限子集{e1,e2,…,en},存在一个连续映射:使得 (f))≥mini∈J(λ)(fei,(λ))对于任意的 λ=(λ1,λ2,…λn)∈ 成立,此时:{i∈{1,2,…,n}|λi>0}.则称函数 f:E×Y→R 在 B 上是广义拟凹的.
定理4.1:设X是LC向量空间 中的一个非空H-紧、H-凸子集.若函数f:X×X→R满足如下条件:
(1)对于任意给定的y∈X,f(x,y)关于x∈X是下半连续的;
(2)对于任意给定的x∈X,f(x,y)关于y∈X在X上是广义拟凹的;
(3)对于任意x∈X,存在给定的γ∈R,使得f(x,x)≤γ.
则存在x*∈X使得对于任意y∈X,f(x*,y)≤γ.
证明:设集值映射 F:X→X 为:对于 y∈X,F(y)={x∈X|f(x,y)≤γ}.则对于任意给定的y∈X,由条件(1)成立可得,F(y)在X中是闭的.又因为对于任意给定的x∈X,由条件(2)成立可得,对于任意X的有限子集{y1,y2,…,yn},存在一个连续映射: →X,使得对于任意λ=(λ1,λ2,…λn)∈,存在f((λ)),(λ)≥mini∈J(λ)f((λ),yi).
此时::={(λ1,λ2,…λn)J(λ):={i∈{1,2,…,n}|λi>0}.
若存在一个 λ0∈ 使得对于任意i∈J(λ0)有,则对于任意i∈J(λ0)有 (f(λ0),y)i>γ.因此 (f(λ0),(λ0),)≥mini∈J(λ0)(f(λ0),y)i>γ.
由于这与对于任意x∈X,f(x,x)≤γ矛盾,则对于任意λ∈,存在i∈J(λ)使得(λ)∈F(yi).由定理2.1可得 .则存在x*∈X使得对于任意y∈X,f(x*,y)≤γ.
五、向量形式的Ky Fan极大极小不等式
定义5.1[9]:设是一个Hausdorff拓扑空间,Z是一个带有锥P的Hausdorff拓扑空间,P是一个非空凸闭的尖锥且int P≠ ,并有A M,Y M.若对于任意有限子集{a1,a2,…,an} A,存在连续映射:→Y,使得对 λ=(λ1,λ2,…λn)∈ ,存在 i∈J(λ)使得 f((λ))∈(fai,(λ))+P,此时 :=({λ1,λ2,…λn) ,λi≥0},J(λ):={i∈{1,2,…,n}|λi>0}.则称函数 f:M×Y→Z 在 A 上是 P-拟凹的.
定义5.2[9]:设是一个Hausdorff拓扑空间,Z是一个带有锥P的Hausdorff拓扑空间,P是一个非空凸闭的尖锥且int P≠ .若对于在Z中任意具有0元的开邻域V,在X中存在一个x0的开邻域U,使得对于任意 x∈U,f(x)∈f(x0)+V+P.则称向量值函数 f:M→Z在x0∈X上是P-连续的.若在X的每一点上f都是P-连续时我们称f在X上是P-连续的.
定理5.1:设X是LC向量空间 中的非空H-紧、H-凸子集.Z是一个带有锥P的Hausdorff拓扑向量空间,P是一个非空凸闭的尖锥且int P≠ .若映射f:X×X→Z满足如下条件:
(1)对于任意给定的y∈X,f(x,y)关于x∈X是P-连续的;
(2)对于任意给定的x∈X,f(x,y)关于y∈X在X上是P-拟凹的;
(3)对于任意x∈X,f(x,x)int P.
则存在x*∈X使得对于任意y∈X,f(x*,y)int P.
证明:设集值映射 F:X→X 为:y∈X,F(y)={x∈X|f(x,y)int P}.对于任意给定的y∈X,设X的网{xα}满足xα→X,xα∈F(y).若x F(y),则f(x,y)∈int P,因此在Z中存在0的开邻域V使得f(x,y)+V int P.由条件(1)可得,对于任意给定的y∈X,X中x的开邻域 U 使得对于 x0∈U,f(x0,y)∈f(x,y)+V+P int P+Pint P,则存在α0使得对于任意α>α0有f(xα,y)∈intP.由于这与 xα∈F(y)矛盾,则 F(y)在 X 中是闭的.
对于任意给定的x∈X,由条件(2)可得,对于任意有限子集{y1,y2,…,yn} X,存在连续映射:→X,使得对 λ=(λ1,λ2,…,λn)∈,存在i(0λ)∈J(λ)使得此时 :=({λ1,λ2,… λn),λi≥0},J(λ):={i∈{1,2,…,n}|λi>0}.若存在 λ0∈,对于任意 i∈J(λ0),使得(λ0)(y)i,则对于任意i∈J(λ0),(f(λ0),y)i∈int P.因此 f(((λ0)),((λ0)))∈f((λ0),+P int P+P int P.由于这与对于任意x∈X,(fx,x)P矛盾,则对于任意 λ∈,存在 (iλ)∈J(λ)使得(λ)∈F(y(iλ)).由定理2.1可得,,则存在x*∈X使得对于任意y∈X,f(x*,y) int P.
[1]Wu X.,Yuan X.Approximate selections,fixed points,almost fixed points of multivalued mappings and generalized quasivariational inequalities in H-spaces[J].Nonlinear Analysis TMA.,1999,(38):249-258.
[2]Horvath,C.D.Extension and selection theorems in topological spaces with a generalized convexity structure[J].Ann.Fac.Sci.Toulouse,1993,(2):253-269.
[3]Horvath C.D.Contractibility and generalized convexity[J].Math.Anal.Appl.,1991,(156):341-357.
[4]Granas,A.,Dugundji,J.Fixed Point Theory[J].Springer,New York,2003.
[5]Yang Z.,Pu Y.J.Generalized Knaster-Kuratowski-Mazurkiewicz TheoremwithoutConvexHull[J].OptimTheoryAppl.,2012,(154):17-29.
[6]Hou,J.C.A Further Generalization of Brouwer-Schauder-Tychonoff Fixed Point Theorem[J].Acta Mathematic Sinica,2002.987-990.
[7]Fu J.Y.,Wang S.H.Generalized Strong Vector Quasi-equilibriumProblemwith Domination Structure[J].J Glob Optim,2013,(55):839-847.
[8]Hou,J.C.Characterization of the existence of pure-strategy Nash equilibrium[J].Appl.Math.Lett.,2009,(22):689-692.
[9]Luo X.Q.Generalized Quasiconcave Mapping and Vector-Valued Minimax Inequalities[J].College Mathematics,2011,27(6):47-51.
[10]Zhang Y.,Cai G.H.,Wang S.H.,Fu J.Y.A minimax inequality equivalenttothegeneralizedKKMtheorem[J].JournalofNanchang University(NaturalScience),2014,38(5):413-416.
