适度拓展教材空间 促进学生数学理解
2015-05-25韩焱龙
韩焱龙


[摘 要]教材是教学的主要课程资源,但不是唯一资源。因此,教师应立足学生实际,创造性地活用教材,对教材进行适度的挖掘、延伸和拓展,做到拓之有理、拓之有据、拓之有度,方能激发学生的学习兴趣,让学生在习得知识、掌握技能的同时,更好地深化数学理解,提升数学素养。
[关键词]认知冲突 核心问题 数学理解 适度拓展
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2015)14-036
叶圣陶先生曾经说过:“教材只能作为教学的依据,要教得好,使学生受益,还得靠老师的善于运用。”这句话告诉我们,教材是教学的主要课程资源,但不是唯一资源。因此,教师要从数学学科固有的知识体系和学生实际出发,创造性地活用教材,对教材进行适度的发掘、延伸和拓展,才能让学生在习得知识、掌握技能的同时,更好地深化数学理解和提升数学素养。下面,笔者就如何处理教材,谈一些自己的实践与思考。
一、适度链接,方能“前后连贯”
数学教材是实施数学教学的重要资源,具有很强的实用性和可塑性。教材给我们呈现的往往只是一堂课中所学知识要点的基本素材,不会出示一个完整的、串联所有知识点的内容,这就需要教师创造性地整合、重组教材,进行适度链接,使教学变得前后连贯。
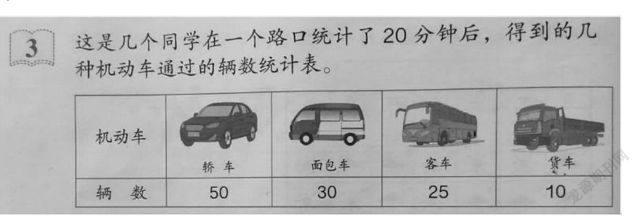
例如,在人教版四年级上册“ ‘以一当五’的条形图”中,教材只是呈现了需要“以一当五”的条形图实例。如下:
这样教学是孤立的,缺少前后链接。要让学生理解“以一当五”和“以一当多”产生的合理性与必要性,就必须通过比较,才会有一个系统、深刻的理解,还可以为后续的数据分析提供必要的素材。为此,教师需对例题进行改变。
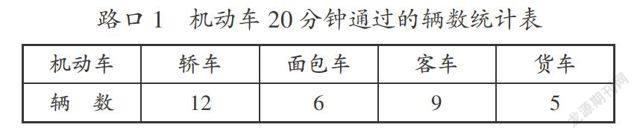
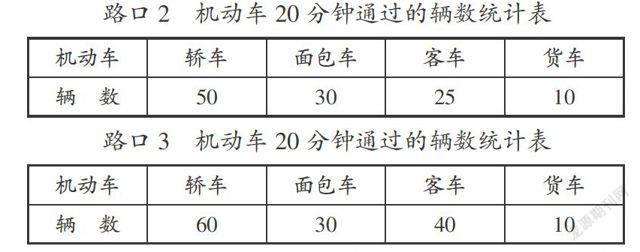
1.谈话引入:韩老师有一位朋友小王在交警支队工作,昨天领导派他到迪荡新城的三个十字路口采集数据,小王分别在三个路口统计了20分钟,得到了四种机动车通过的辆数。
2.把小王采集的数据填入统计表,再猜一猜:小王是用什么方法采集数据的?
3.根据数据特征确定制图时需“以一当几”,再完成三幅条形图。
4.补充教学内容,让学生进行数据分析:猜猜交警支队为什么要对三个路口进行车流量统计,再说说支队长会对数据作怎样的分析。如果你是支队长,你会采取什么措施?
统计课程的核心是发展学生的数据分析观念,而发展数据分析观念的首要任务是培养学生对数据的情感,使他们知道数据能帮助人们做事,通过数据进行判断比瞎猜要好,且这个数据自己也能够得到。
重组教材,适度链接,可以使教学前后连贯,促进学生的数学理解。同时,可以激发学生的学习兴趣,有利于学生对知识的整体建构和应用水平的提高。
二、适度超越,方能“深刻领悟”
在教学中,我们习惯被《数学课程标准》和《教师教学用书》中规定了的教学目标限制着,似乎脱离了这两根缰绳就是离经叛道。然而,笔者以为,在达成规定的教学目标外,适度超越教材,提出引人思考的核心问题,可以激发学生探究的欲望,提升学生的思维张力。
例如,在教学人教版五年级下册“3的倍数的特征”时,大多教师都会制订让学生发现、掌握3的倍数的特征的主要教学目标,而忽视了引导学生深入研究3的倍数的特征存在的合理性和科学性。
课堂教学中,在学生通过观察探究出3的倍数的特征后,教师不妨出示111这个数让学生思考:“111是3的倍数吗?为什么?”学生自然会说:“一加一加一等于三,所以111是3的倍数。”此时,教师不妨提出这样一个核心问题:“为什么各数位上的数的和是3的倍数,这个数就是3的倍数呢?”然后教师引导学生用“拆开来看余数”的方法深入研究以下问题:100除以3有余数几?10除以3有余数几?1除以3有余数几?111除以3会有余数吗?接着,教师再出示一些数,如222、531、789、456等,让学生用同样的方法进行研究,使学生通过不完全归纳法得出各数位上的数就是它们除以3的余数,所以各数位上的数的和是3的倍数,这个数就是3的倍数。
有时设置一个教材中没有提到的,《教师教学用书》中也没有要求的,但学生能通过思考解决的核心问题(知识的重难点或思维的“最近发展区”),让学生透过现象看本质,不仅能使学生彻底领悟知识存在的合理性和科学性,更重要的是课堂教学因此变得深刻,学生的思维习惯或许会由此而改变,质疑能力和数学素养也会由此得到提升。
三、适度跳跃,方能“困境突围”
在课堂教学中,教师提出的问题往往不止一个,在这一系列的问题中,常常会有一个起到统摄作用的核心问题,这个核心问题对知识的掌握具有核心意义,作用非同一般。因此,教师应适度跳出教材的限制,找准核心问题,在学生的认知范围内引发认知冲突,让学生在思辨中进行认知“突围”。这样不仅会促进学生的数学理解,还能使他们的思维向纵深发展。
例如,在教学人教版四年级上册“利用商不变的规律简便计算”时,教师对例9(780÷30)和例10(840÷50)进行了改进,出示240÷20和250÷20这一组便于比较的习题让学生列竖式计算,接着让学生讨论这一组题的异同点,再启发学生利用商不变的规律进行竖式计算。如下:
当学生发现“250÷20=25÷2”的商无法写时,都感到这太奇怪了,接着教师引导学生思考商无法写的原因。有的学生认为商不变的规律只是说商不变,并没有说余数不变;有的学生后来又发现被除数和除数都除以10,虽然商不变,但余数也要除以10,由10变1。于是,教师顺势抛出一个核心问题:“250÷20和25÷2是相等的,商一定能用同一个数来表示,这究竟是一个怎么样的数?”同时,教师在黑板上把余数和除数一连,再提问:“余数和除数之间有什么关系?”这时,学生顿悟:两个余数都是除数的一半,商可用我们没学过的小数12.5表示。
上述教学中,教师不拘泥于教材,有意把“250÷20=25÷2=?”融入教学中,让学生进入“陷阱”并探索突围,为学生构建了一个思维不断演进的生态场,使学生深刻理解学习内容,从而促进学生的思维向纵深发展。
四、适度念旧,方能“永不相忘”
从现有认知水平出发,进行知识迁移,是获取知识的最佳途径之一。迁移不仅可以使知识前后连贯、更易理解,还能使知识变得有厚度、更深远。
例如,教学人教版四年级下册“乘法运算定律”一课时,教材设置了一幅植树的情境图:“一共有25个小组,每组里有4人负责挖坑、种树,2人负责抬水、浇树。一共有多少名同学参加了这次植树活动?”在实际教学中,不少教师会照搬教材,复制情境,引导学生用两种不同的思路进行解答,从而得出25×(4+2)=25×4+25×2,为概括乘法分配律打下基础。
乘法分配律被称作乘法对加法的分配性质,既是沟通加法和乘法两种运算之间联系的运算定律,又是小学阶段学生最难理解和掌握的定律。如果能找出一个思维的“最近发展区”,沟通其与乘法分配律的联系,再让学生自主探索出乘法分配律,那学生肯定会学得容易且深刻。
为此,教师弃用教材情境,创编了这样一道题:“一副羽毛球拍要44元,购买25副羽毛球拍要多少元?”列式后教师先让学生估算,再用竖式计算,并让学生说出竖式中每一步的含义。
接着教师让学生说说怎么口算25×44,在学生获得对乘法分配律的理性认识后,再引导学生把竖式改写成横式,即25×44=25×(□+□)=25×□+25×□=□+□=□,进而得出乘法分配律。
这样多算结合,由旧推新,直接把竖式计算迁移到乘法分配律中,实现了旧知对新知的顺应,促进了学生的数学理解,这样的理解才会“永不相忘”。
总之,教师应充分认识教材的重要性和严肃性,但不要把理解教学内容等同于领会编者意图,因为后者怎么说也是他人的想法,可以借鉴,但不能盲从,我们得有自己的想法。但是,我们也要清楚,教材的发掘和拓展不是一种装饰,更不应该成为教学的累赘,而应该立足学生实际,体现学科精神,服务教学需要,做到拓之有理、拓之有据、拓之有度,方能激发学生的学习兴趣,促进学生的数学理解和提升数学素养。
(责编 杜 华)
