时滞Lorenz-like系统的Hopf分岔研究*

王志强，王书玲，吴然超

(安徽大学数学科学学院，合肥 230601)

时滞Lorenz-like系统的Hopf分岔研究*

王志强，王书玲，吴然超＊＊

(安徽大学数学科学学院，合肥 230601)

随动力系统学的发展，平衡点的稳定性以及Hopf分岔对于动力系统学研究愈显重要。首先研究时滞Lorenz-like系统存在平衡点的条件，在此条件下，通过分析系统在平衡点处的线性化系统特征根的分布情况，得出系统在平衡点处的稳定性;随着系统时滞参数的变化，时滞系统在平衡点处稳定性相应地会发生改变;以时滞为分岔参数，研究了时滞系统存在Hopf分岔的条件;最后利用Matlab程序进行仿真，验证了理论分析的正确性。

Lorenz-like时滞系统;稳定性;极限环;Hopf分岔

0 引 言

稳定性与分岔问题是动力系统研究中的重要课题之一，国内外已较好地掌握了相关的数学分析工具［1］，在稳定性与分岔的理论研究和工程应用方面取得长足的进展［2］。动力系统的分岔是指，在系统参数发生连续变化的情况下，如果系统相轨迹的拓扑结构发生了改变，称这种变化为分岔。考虑含参数的动力系统

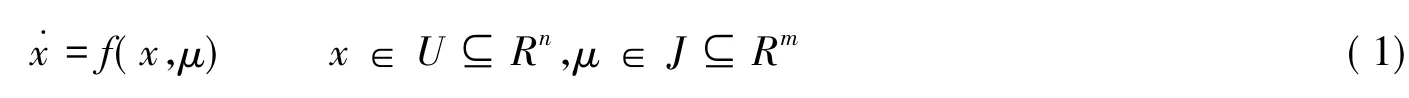
其中μ是实分岔参数，f是关于x和μ的函数。当参数μ连续变动时，如果上述系统的拓扑结构在μ0∈J处发生突然变化，称该系统在μ=μ0处出现分岔，μ0称为系统的一个分岔值，分岔值组成的集合称为分岔集。Hopf分岔是较为常见、应用较广泛的一种分岔类型［3］，它是指当分岔参数变化且经过分岔值时，从平衡状态产生孤立的周期运动的现象。从相图上看，这时有极限环从平衡点“冒”出来。

自从1963年气象学家Lorenz提出经典的Lorenz系统［4］以来，大量的混沌系统相继被提出，例如Chen系统［5］，Liu系统［6］，T系统［7］等。近年来，对这些系统分岔问题的研究已成为热点之一，其中关于Hopf分岔问题的研究有很好的结果，相关研究也被应用到物理学、生物学、化学等众多学科领域。在文献［8］中，提出了一个新的Lorenz类系统，并研究了它的分岔规律，系统的动力学方程为

其中x，y，z为状态变量，a，b，c，d为系统参数。系统含有6项，其中有4个线性项，与较其它的混沌或超混沌系统相比，系统的结构形式较为简单，这为电路实现带来方便。因此，系统在保密通信等领域具有潜在的应用价值。

在流体系统中，蒸气和流体在管道中的流动具有延迟;在通信系统中信号的传输会发生拥挤阻塞等现象;在种群生态系统中，捕食者在具有捕食能力之前大都需要一定的成长时间和成熟时间，因此，时滞在动力系统中是普遍存在的。基于这样的考虑，Lorenz类系统(2)中，给状态变量施加时滞得到一个三维时滞系统，称之为时滞Lorenz-like系统。

在Lorenz系统中考虑时滞现象，构造一个时滞Lorenz-like系统为

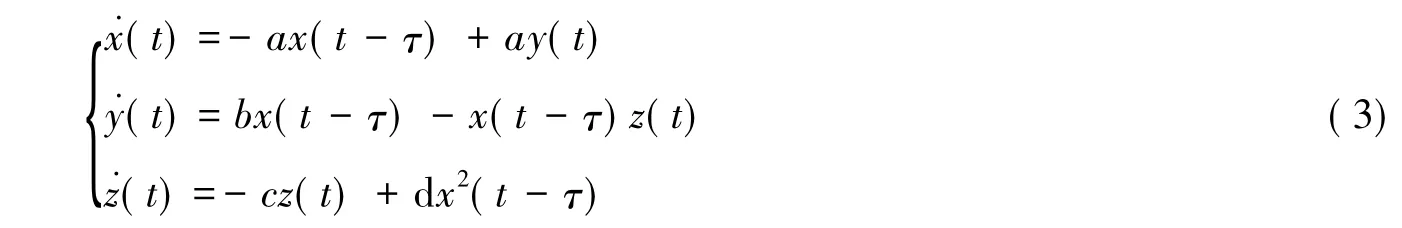
其中τ(＞0)为时滞，可以理解为蒸气或流体在管道中的流动延迟时间、信号传输的阻碍时间，也可以理解为捕食者的成熟所用的时间(生物生长周期)。

系统(3)具有3个平衡点，它们分别为

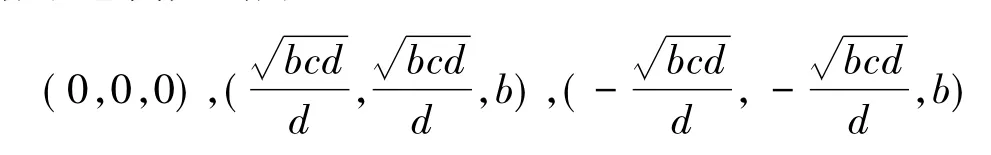
当系统(3)的参数a＞0、b＜0、c＞0、d＞0时，系统(1)具有唯一的平衡点O(0，0，0)。在此参数条件下，考虑系统(3)在平衡点O(0，0，0)处的稳定性以及Hopf分岔的存在性。

1 时滞Lorenz-like系统在平衡点的稳定性及其Hopf分岔

定理1 如果a＞0、b＜0、c＞0、d＞0，那么，

(1)当τ∈［0，τ0)时，系统(1)的平衡点O(0，0，0)是渐近稳定的;

(2)当τ＞τ0时，系统(1)的平衡点O(0，0，0)是不稳定的;

(3)当τ=τk(k=0，1，2，3，…)时，系统(1)在平衡点O(0，0，0)处发生Hopf分岔。

要证此定理，需要下述关于Hopf分岔存在条件的引理。

引理［3］假设系统 ˙x=f(x，μ)在平衡点x0(μ)处的Jacobian矩阵具有一对虚特征根λ1，2=α(μ)±iω(μ)和实数根λj(μ)。若对于μ=μ0，成立下列各式

则μ=μ0为系统的Hopf分岔值，在μ＜μ0(或μ＞μ0)时，系统将产生一簇围绕平衡点x0(μ)的极限环。

定理1的证明过程分为以下4个命题。系统(3)在平衡点O(0，0，0)处线性化系统为

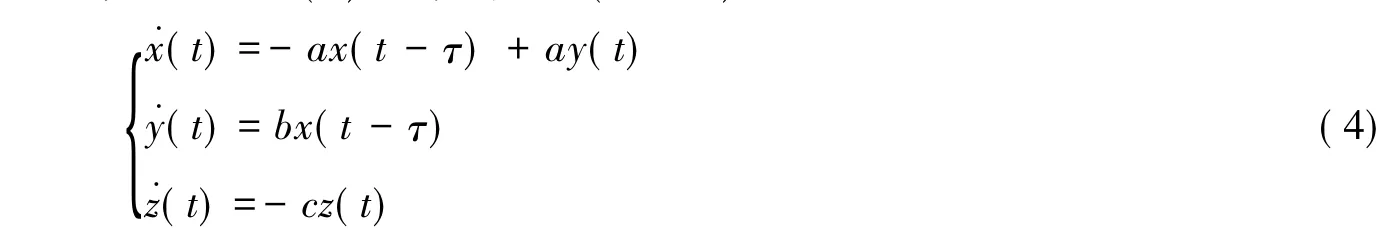
线性系统(4)对应的特征方程为

命题1 若τ=0，则系统(3)的平衡点O(0，0，0)是局部渐近稳定［9］的。

证明 当τ=0时，特征方程(5)转化为

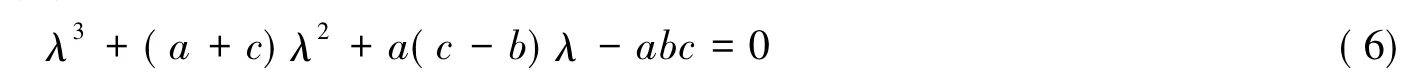
因为参数a＞0、b＜0、c＞0、d＞0，所以易知(a+c)＞0，a(c－b)＞0，－abc＞0。

根据Routh-Hurwitz定理［9］可知，特征方程(4)的所有根都具有负实部。所以当τ=0时，系统(3)的平衡点O(0，0，0)是局部渐近稳定的。

证毕。

命题2 当τ＞0时，方程(5)存在一个纯虚根λ=iω(ω为一个正常数)。

证明 由于只考虑虚根，方程(5)与以下方程等价

则虚部ω满足

于是，

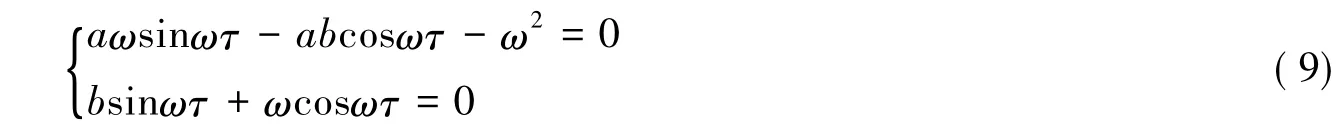
方程(9)可化为

接下来只需证，对于方程(10)至少有一个正实根。令u=ω2，则方程(10)可化为

设g(u)=u2－a2u－a2b2，不妨设g(u)=0的根为u1和u2，则由韦达定理易知

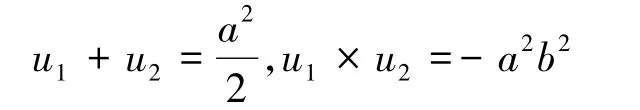
显然u1，u2满足u1×u2＜0，即g(u)=0必有一正实根，不妨设为u'＞0，此时有g(u')=0从而，显然方程(10)至少有一个正实根。

证毕。

命题3 存在τk≠0，使得方程(5)的特征根λ(τ)=α(τ)+iω(τ)，满足α(τk)=0，ω(τk)=ω0。

证明 设ω0为方程(10)的一个正实根，则方程(7)有一纯虚根iω0。又由方程组(9)得

将ω=ω0代入方程(12)，则时滞τ的值为

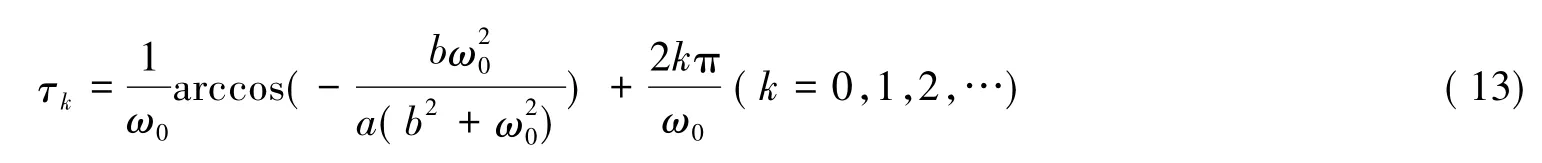
因此(iω0，τk)是方程(7)的解，即λ=±iω0是时滞 τ=τk时方程(5)的一对共轭的纯虚根。设τ0= min{τk}，则时滞τ=τ0是使得方程(5)出现纯虚根λ=±iω0时τ的最小值。

证毕

证明 在方程(7)两边同时对τ求导，得

易得，

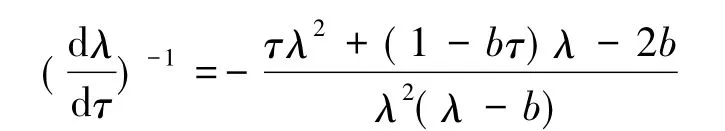
因为λ(τk)=iω0，所以有

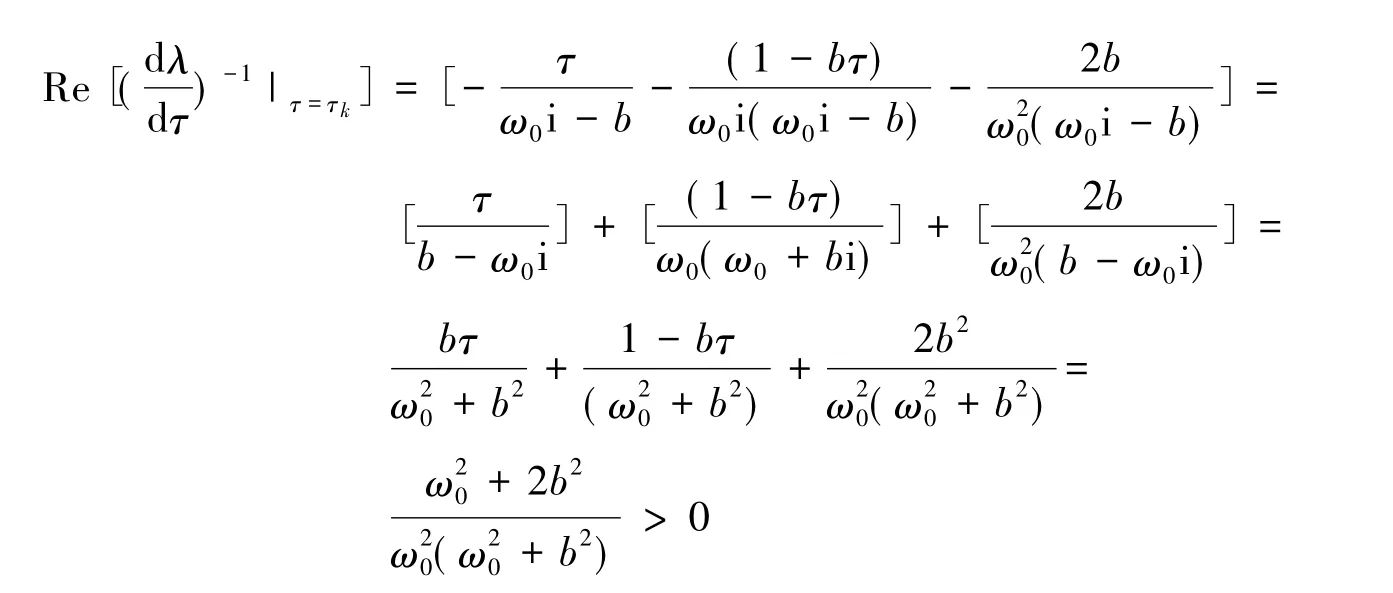
即

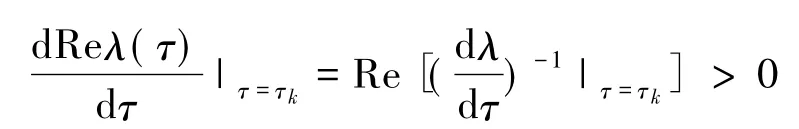
证毕。

综上所述，根据引理，定理1成立。

2 数值仿真

因为参数a＞0、b＜0、c＞0、d＞0，不妨取a=c=d=1，b=－1，这时系统为

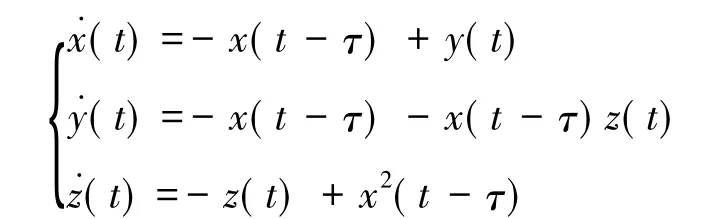
利用Matlab软件计算得，由ω4－a2ω2－a2b2=0，得ω0=1．272;再由，得τ0= 0．711 1。因此，由定理1可得下面的推论。

推论若a＞0、b＜0、c＞0、d＞0，则

(1)当τ∈［0，0．711 1)时，系统的平衡点O(0，0，0)是渐近稳定的;

(2)当τ＞0．711 1时，系统的平衡点O(0，0，0)是不稳定的;

(3)τ=0．711 1+1．572 3kπ (k=0，1，2，3，…)是系统的Hopf分岔值，即系统(2)在平衡点O(0，0，0)处发生Hopf分岔，产生极限环。

利用Matlab软件，给出时滞τ取不同值时的系统的状态变量随时间t的轨线图和相图。由图1可以看出，当时滞τ=0．7时，系统的状态变量x，y，z的值随时间t的逐渐增大而趋于平衡点O(0，0，0)，所以平衡点O(0，0，0)是渐近稳定的。由图2知，当时滞τ=0．711 1时，系统的状态变量x，y，z的值随时间t的增大永远保持周期震荡，说明系统在平衡点O(0，0，0)处发生了Hopf分岔，在相空间O－xyz上出现了极限环。

由图3可以看出，系统的状态变量x，y，z的值随时间t增大而逐渐远离平衡点，所以当时滞τ=0．72时，系统的平衡点O(0，0，0)是不稳定的。

3 总 结

研究了时滞Lorenz-like系统在平衡点处的稳定性与Hopf分岔。通过理论分析，给出了时滞Lorenz－like系统在平衡点处渐进稳定的条件，以及发生Hopf分岔的条件。数值模拟验证了理论分析的正确性。通过对时滞Lorenz－like系统的稳定性与Hopf分岔分析，说明该时滞系统具有较丰富的动力学性态，为系统在实际中应用提供理论基础。

图1 τ=0．7，x(t)=0．01，y(t)=0．02，z(t)=0．01 (t∈［－0．7，0］)时，x，y，z随t的轨线

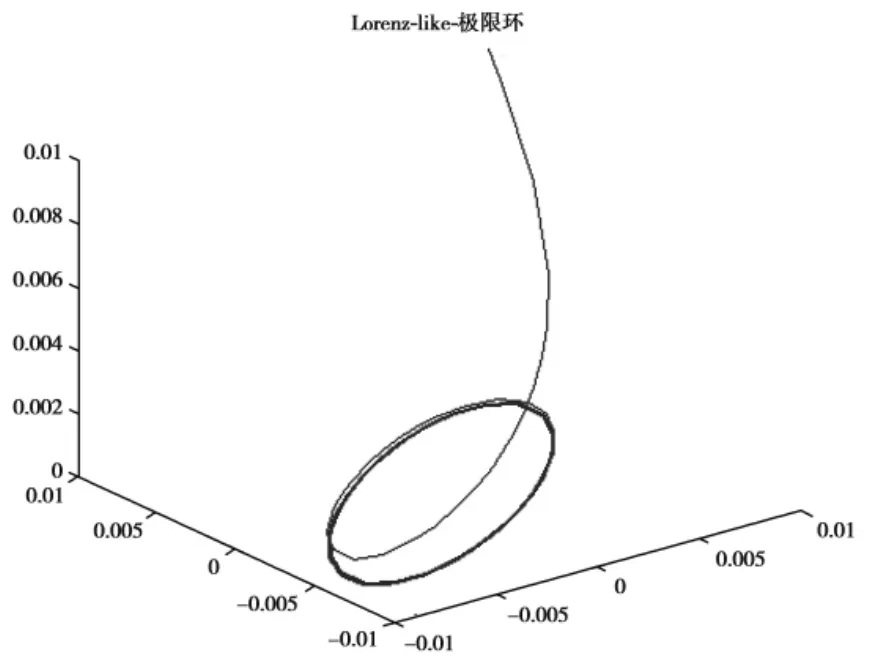
图2 当τ=0．711 1，x(t)=y(t)=z(t)=0．01 (t∈［－0．3，0］)时，系统的相图

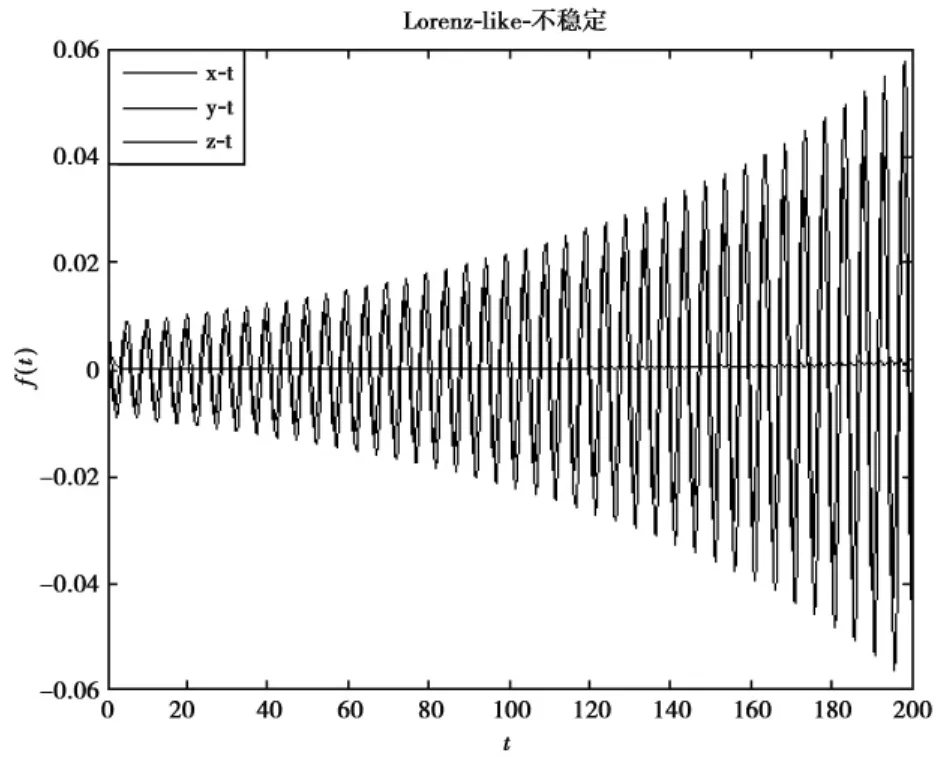
图3 当τ=0．72，x(t)=y(t)=z(t)=0．01 (t∈［－0．72，0］)时，x，y，z随时间t的轨线

［1］TAN C W，VARGHESE N，VARAIYA P．Bifurcation chaos and voltage collapse in power systems［J］．Proceedings of the IEEE，1995，83:1484-1496

［2］王庆红，周双喜．电力系统奇异摄动模型霍普夫分岔分析［J］．中国电机工程学报，2003，23(8):1-6

［3］HASSARD B，KAZARINOFF N，WAN Y．Theory and Application of Hopf Bifurcation［M］．Cambridge:Cambridge University Press，1982

［4］ROSSLER Q E．An equation for continuous chaos［J］．Phys Lett A，1976，57:397-398

［5］CHEN G，UETA T．Yet another chaotic attractor［J］．International Journal of Bifurcation and Chaos，1999(9):1465-1466

［6］LIU C，LIU T，LIU L．A new chaotic attractor［J］．Chaos，Solitons＆Fractals，2004，22:1031-1038

［7］TIGAN G．Analysis of a 3D chaotic system［J］．Chaos，Solitons＆Fractals，2008，36:1315-1319

［8］MELLO L F，MESSIAS M，BRAGA D C．Bifurcation analysis of a new Lorenz-like chaotic system［J］．Chaos，Solitons＆Fractals，2008，37:1244-1255

［9］马知恩，周义仓．常微分方程定性与稳定性方法［M］．北京:科学出版社，2005

Research on Hopf Bifurcation of Lorenz-like Delay System

WANG Zhi-qiang，WANG Shu-ling，WU Ran-chao
(School of Mathematical Science，Anhui University，Hefei 230601，China)

With the development of power system，the stability of the equilibrium point and Hopf bifurcation are more and more important to the research on power system．This paper at first studies the condition for the equilibrium point existence in Lorenz-like delay system．Under this condition，the stability of the system at the equilibrium point is obtained by the analysis of the characteristic root distribution of the linearized system at the equilibrium point of the system．With the changing of delay parameters of the system，the stability of the delay system at the equilibrium point can change corresponding，and the condition for the existence of Hopf bifurcation of this delay system is studied by taking delay as bifurcation parameter．Finally the simulation by Matalb program tests the validity of the theoretical analysis．

Lorenz-like delay system;stability;limit cycle;Hopf bifurcation

O175

A

1672－058X(2015)02－0011－06

10．16055/j．issn．1672－058X．2015．0002．003

责任编辑:田 静

2014－08－29;

2014－09－01．

高等学校博士学科点专项基金(20093401120001);安徽省自然科学基金(11040606M12);安徽大学“211项目”

(KJJQ1102)资助项目．

王志强(1993-)，男，安徽安庆人，从事微分方程与动力系统研究．

＊＊通讯作者:吴然超(1971-)，男，安徽六安人，教授，博士，从事微分方程与动力系统研究．Email:rcwu@ahu．edu．cn．