基于比较系统的永磁同步电机的脉冲稳定性*
2015-05-25郭云云
郭云云
(重庆师范大学数学学院,重庆 401331)
基于比较系统的永磁同步电机的脉冲稳定性*
郭云云
(重庆师范大学数学学院,重庆 401331)
永磁同步电动机具有体积小,损耗低,效率高等优点,在节约能源和环境保护日益受到重视的今天,对其研究就显得非常必要;然而与普通的非线性系统相比,永磁同步电机对外部负载扰动和参数变化非常敏感,因此主要通过脉冲控制方法来探究永磁同步电机的稳定性问题,得出了其渐进稳定的充分条件,并通过具体实例来验证结果的有效性.
永磁同步电机;脉冲控制;渐进稳定
1 永磁同步电机的脉冲建模
永磁同步电机的脉冲控制模型:
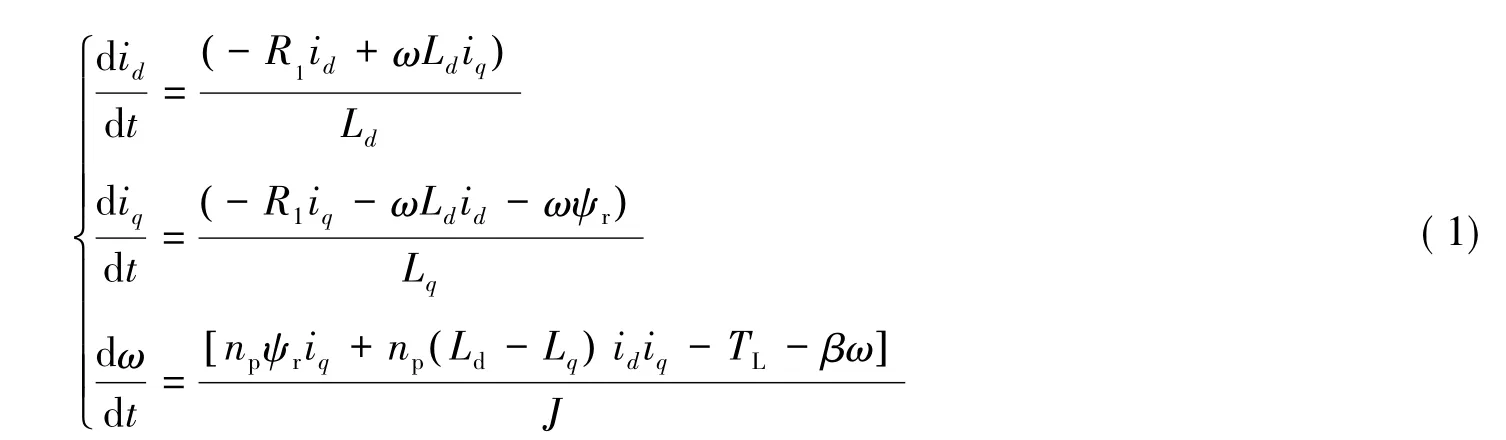
模型(1)中,id,iq分别为d-q轴电流;Ld,Lq分别为d-q轴定子电感;R1表示定子绕阻;ω表示转子角频率;TL表示外部转矩;ψr表示永久磁通;np表示极对数;β表示粘性阻尼系数;J表示转动惯量.
通过仿射变换和时间尺度变换,将模型(1)变换成无量纲的状态方程.即,其中:
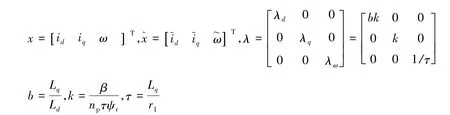
则无量纲的状态方程为
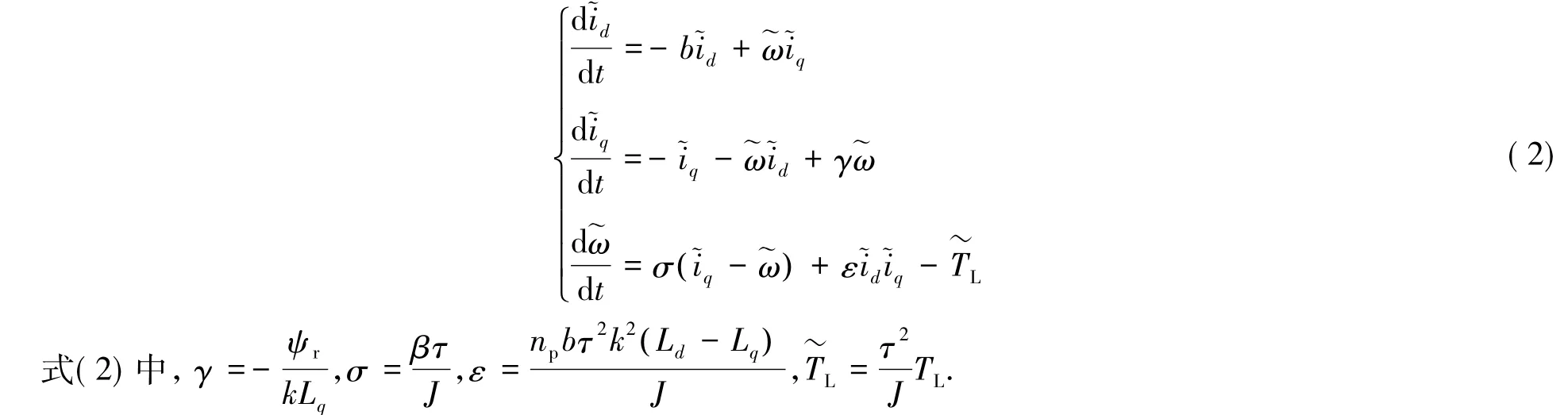
考虑气隙均匀的永磁同步直线电动机混沌模型,即Ld=Lq=L,考虑其中参数的不确定性,并设 x=,则气隙均匀的参数不确定永磁同步电动机混沌数学模型可写为

其矩阵表示如下:

2 预备知识
定义1 令V:R+×Rn→R+,称V属于V0,如果:
(1)V在区间(τi-1,τi]×Rn上连续,且对任一存在;
(2)V关于X满足局部Lipschitz条件.
定义2 考虑如下的脉冲控制系统

令V∈V0,并且满足,其中g:R+×R→R,在区间(τk-1,τk]×R上连续,且对任一)存在;ψk是R+→R+上的不减函数,则系统:

称为系统(5)的比较系统.
定理1[1]对系统(5),如果
(1)f(t,0)=0,u(t,0)=0,g(t,0)=0,对所有k满足U(k,0)=0;
(2)V:R+×Sρ→R+,ρ>0,V∈V0,d+V(t,x)≤g(t,V(t,x)),t≠τk;
(3)存在一个ρ0>0,则对所有k,x∈ρ0蕴含着x+U(k,x)∈Sρ,且V(t,x+U(k,x))≤ψk(V(t,x)),t=τk,x∈Sρ0;
(4)在R+×Sρ上满足上的连续且严格递增函数,K(0)=0),则比较系统(6)平凡解的稳定性蕴含系统(5)的平凡解的相应的稳定性.
3 永磁同步电机的脉冲稳定性
考虑带有脉冲控制的永磁同步电机模型:

定理2 令P是n×n对称正定矩阵,λ1>0,λ2>0分别为P的最小与最大特征值;令Q=PA+ATP;q,d分别为矩阵P-1Q,P-1(I+BT)P(I+B)的最大特征值,0≤δk=τk-τk-1<∞(k=1,2,…)为脉冲间距,则系统(3)是渐进稳定的,如果存在一个常数γ>1满足:qδk≤-ln(γd).
证明 令V(t,x)=xTPx,则当t≠τ时

当t=τi时,V((τi,x+Bx))=xT(I+BT)P(I+B)x≤dV(τi,x),则定理1的条件3就满足了,且ψk(ω)=dω.

令ω(t)为系统(6)在满足初始条件ω(τ+0)=ω0的任一解,则可以得出:
当t∈(τk,τk+1]时,ω(t)=dkω(τ0)exp(q(t-τ0)),又qδk≤-ln(γd),即dexp(qδk)≤1 γ,则:
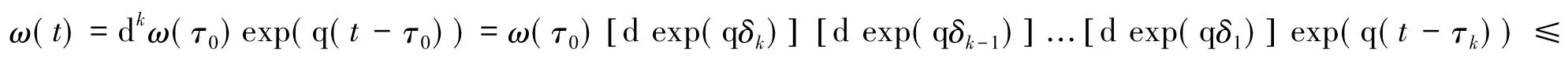
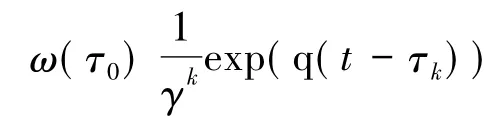
而γ>1,故当t→∞时,k→∞,ω(t)→0,定理得证.
4 数值仿真实验
考虑如下的参数不确定的永磁同步电机
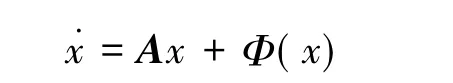


图1 未加控制状态
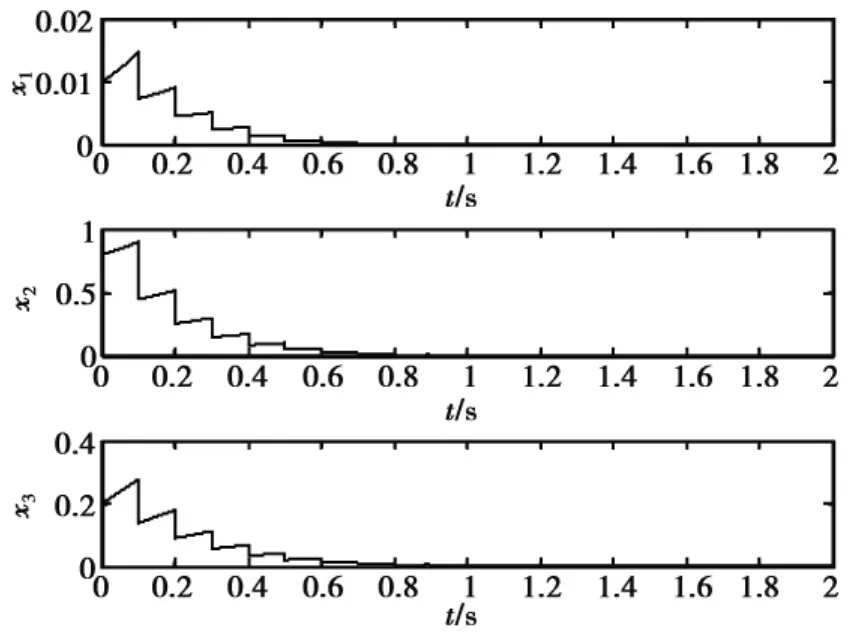
图2 加入脉冲控制状态
δk=δ=0.1,γ=1.3,则qδk≤-ln(γd)满足,加入脉冲控制后,其状态见图2,从图2可知,系统在定理所示的条件下是稳定的.
[1]YANG T.Impulsive control theory[M].Springer,2001
[2]LI D,WANG S L,ZHANG X H.Fuzzy Impulsive Control of Permanent Magnet Synchronous Motors[J].ChinPhys,2007,18:25-401
[3]LI D,WANG S L,ZHANG X H.Impulsive Control of Permanent Magnet Synchronous Motors with Parameters Uncertainties[J].Chin Phys,2008,19(7):121-128
[4]LU Z,CHI X,CHEN L.Impulsive Control Strategies in Biological Control of pesticide[J].Theoretical Population Biology,2003,64 (1):39-47
[5]YANG T,CHUA L O.Practical Stability of Impulsive Synchronization between Two Nonautonomous Chaotic Systems[J].International Journal of Bifurcation and Chaos in Applied Sciences and Engineering,2000(10):859-867
[6]YE H,MICHEL A N,HOU L.Stability Analysis of Systems with Impulse Effects[J].IEEE Trans on Automat Control,1998,43(1) 1719-1723
Impulsive Stability of Permanent Magnetic Synchronous Motor Based on Comparative System
GUO Yun-yun
(School of Mathematics,Chongqing Normal University,Chongqing 401331,China)
It's necessary to researth permanent magnetic synchronous motor with the advantages such as small volume,low wastage,high efficiency and so on,because energy conservation and environment protection are currently more and more emphasized.Compared with common nonlinear system,however,the permanent magnetic synchronous motor is very sensitive to external load perturbation and parameter change,thus,the stability of permanent magnetic synchronous motor is studied mainly by impulsive control method,the sufficient condition for its asymptotic stability is obtained,and the validity of the results is verified by real examples.
permanent magnetic synchronous motor;impulsive control;asymptotic stability
O192.1
A
1672-058X(2015)02-0001-04
10.16055/j.issn.1672-058X.2015.0002.001
责任编辑:田 静
2014-07-18;
2014-09-18.
国家自然科学基金(61302180);重庆市教委基金资助(KJ130606).
郭云云(1989-),女,山西临汾人,硕士研究生,从事微分方程与动力系统方向研究.
