一种改进的遗传退火算法以及收敛性分析*

高发玲

(青岛理工大学琴岛学院，山东 青岛 266100)

一种改进的遗传退火算法以及收敛性分析*

高发玲

(青岛理工大学琴岛学院，山东 青岛 266100)

针对一种约束条件既有0－1变量又有整数变量的非线性混合整数规划模型，给出一种改进的遗传退火算法求解，并建立对应的Markov链且理论证明其收敛性．

遗传退火;Markov链;遍历;收敛性

0 引 言

针对一种约束条件既有0－1变量又有整数变量的非线性混合整数规划模型，数学模型

提出一种改进的遗传退火算法并对其算法对应Markov链进行收敛性分析．

1 算法设计

改进的遗传退火算法分为5步:编码方案的设计、解除约束与适应度函数的选定、交叉操作设计、变异操作设计以及终止条件的确定．

1．1 编码方案的设计

对于0－1决策变量的Y，采用二进制编码;对于整数变量X，采用浮点编码．

1．2 解除约束与适应函数的选定

(1)约束优化问题处理．采用惩罚策略技术将有约束的优化模型转化为无约束优化问题，

此时采用的可变惩罚因子a=tk，其中tk为第k代退火温度．

(2)适应度函数的选定．

1．3 交叉操作设计

由于编码方法采用的是上述混合并行方案，因此在交叉操作中也采用相应的方式，对0－1决策变量的Y进行单点交叉，对整数变量X进行混合交叉．

1．4 变异操作设计

对模型中的两种决策变量采用不同的变异方式，对0－1决策变量的Y采用基本位变异，对整数变量X采用均匀变异．

1．5 终止条件的确定

计算在每一温度下每一代群体染色体的最大适应值和最小适应值，当最大适应值与最小适应值之间的差小于ε(ε为参数)时，停止此温度下的种群迭代;设退火温度为tk，若满足tk≤η(η为很小的参数)时(计算迭代到规定的退火温度)，则停止计算．

2 算法收敛性分析

2．1 算法对应Markov链的建立

离散组合优化问题minf(bi)，其中bi为所有变量对应的一个状态，设状态集

设变量的个数为k(其中有l个0－1变量;有k－l个整数变量)，称为一个个体或染色体，这里的为整数．

引理1［2］若C和M分别是以交叉概率Pc∈[0，1]进行交叉和以变异概率Pm∈(0，1)进行变异对应的一步转移概率矩阵，则C和M均为随机阵．

定义2 若种群B(i)和B(j)中仅有某一个个体不同，设bi∈B(i)≠bj∈B(j)且满足bj∈N(bi)，则称种群B(i)属于种群B(j)的邻域N(B(j))．

定义3 SA状态产生函数使种群B(i)转移到B(j)的一步转移概率为

其中

定义4 对种群中个体作模拟退火操作所引起的种群的一步转移概率:

则在温度T下对所有个体均作模拟退火操作得到的种群转移概率为

此时A(T)阵是随机阵．

因此，此种改进的遗传退火算法在每一温度下的状态转移矩阵为

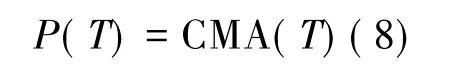
从而得到所建立的遗传退火算法对应的Markov链可表示如下:

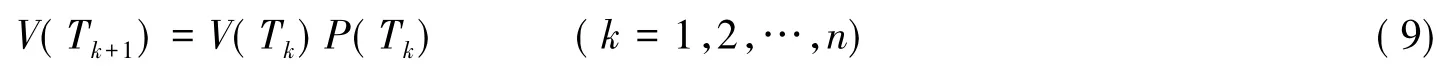
2．2 收敛性分析

定义5［2］给定随机阵，其遍历系数定义为

定义6 给定图G的中心Ic，若Q中任意节点到达Ic最多经过步，则称r为图G的半径．其中d(i，j)为种群B(i)到达B(j)的最短路径

引理2 若算法对应的有限非齐次Markov链在每一温度Ti下存在平稳分布，则在每一温度Ti下状态转移矩阵P(Ti)存在特征值为1的左特征向量．其中

证明

(1)若在每一温度Ti下Markov链存在平稳分布π(Ti)，则由平稳分布定义知

(2)由引理1及式(7)知算法中每一温度Ti下的转移矩阵P(Ti)均是随机矩阵，必得它的平稳分布π(Ti)的每一分量均为正数，从而知等价于，再由范数定义［3］知

由(1)、(2)可得证引理2成立．

证明 由定理2知Markov链强遍历的充分必要条件是Markov链弱遍历且在每一温度下状态转移矩阵存在特征值为1的左特征向量且

所以分为3步来证明定理:第一步，证明Markov链的弱遍历性;第二步，证明每一温度下状态转移矩阵存在特征值为1的左特征向量;第三步，证明

第一步:证明Markov链的弱遍历性．

当B(i)∈(Q－Qm)时，若B(j)∈N(B(i))，则

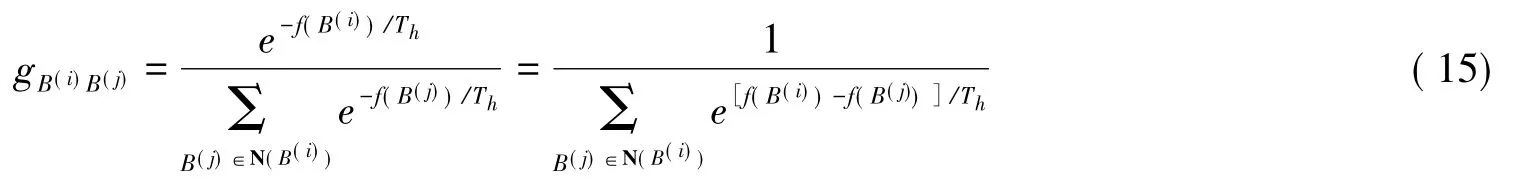
由式(11)知当 B(i)∈ (Q －Qm)时，f(B(i)) ＜ f(B(j))，从而此时的 gB(i)B(j)是随着 h的增大而增大，而是随着h的增大而减小，进而得aB(i)B(j)(Th)随h的增大而减小;若且 B(j)≠ B(i)，则从而得当 B(i)∈ (Q － Qm) 时，随h的增大而增大;即存在整数k0，k0＜∞，对所有的B(i)∈(Q－Qm)，都有

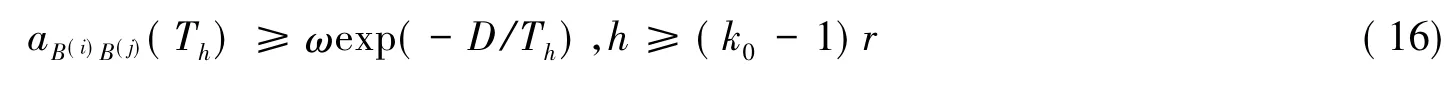
所以，∀B(i)∈Q，h≥k0r

C，M，A(T)均为随机阵，得每一温度下的状态转移阵P(T)=CMA(T)也是随机阵，且τ(P)≤τ(A)，从而

即

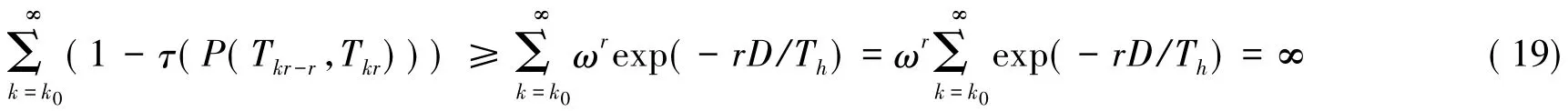
第二步:证明每一温度下状态转移矩阵存在特征值为1的左特征向量由引理2知只要有限非齐次Markov链在每一温度Ti下存在平稳分布，即平稳分布就是所要找的π(Ti)，所以问题就转变为平稳分布的证明，而不可约非周期Markov链存在平稳分布［4］，下面分为两步来分别证明Markov链不可约非周期性．现证明Markov链的不可约性及非周期性．

(1)由设计的算法中的交叉和变异方式知∀B(i)，B(j)∈Q，cB(i)B(j)，mB(i)B(j)均大于0，由式(4)和(6)知∀B(i)，B(j)∈Q，存在z≥1使得B(i)，B(k)，B(k+1)B(z)，B(j)∈Q，满足:

所以当温度T＞0给定时，∀B(i)，B(j)∈Q，算法对应的有限状态的非齐Markov链有

因此，B(i)↔B(j)，进而由状态B(i)和B(j)的任意性知B(i)↔B(j)．从而，由不可约的充分条件可得到算法对应的Markov链是不可约的．

(2)由式(4)知∃B(j)≠B(i)∈Q，且B(j)∈N(B(i))，使得

而且又满足

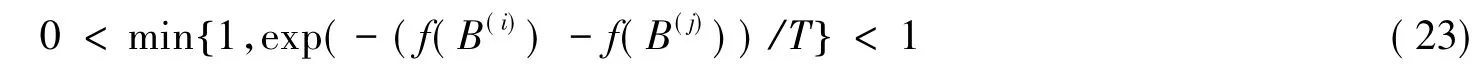
由式(6)得

则状态∀B(i)∈Q到自身的转移概率

由(1)(2)知算法对应的Markov链存在平稳分布，进而由引理2得出在每一温度下状态转移矩阵存在特征值为1的左特征向量

由式(5)及第一步证明过程知当j∈Q－Qm且k∈N(j)时，aj，k(Th)随着的增大而减小，所以当j∈Q－Qm且k∈N(j)时，存在N∈Z+，使的n＞N时有

所以，取n0=max{M，N}，由式(26)、(27)、(28)得，当n＞n0时，

成立．又由定理中的假设知存在n1，使得n≥n1时，满足

而由范数定义［3］知

取n'=max {n0，n1}，由式(29)、(30)、(31)得，当n≥n'时，

成立．因此，由第一、二和三步的证明以及文献定理［2］可证得此定理成立．

3 结 论

对于有约束非线性混合整数规划方程，提出了一种改进的遗传退火算法求解方法．通过建立算法对应的Markov链并对其收敛性给出理论证明．

［1］陈斌，王晓．基于遗传算法的可再用逆向物流网络规划研究［D］．上海海事大学，2006

［2］王凌，郑大钟．一类GASA混合策略及其收敛研究［J］．控制与决策，1998，13(6):669-672

［3］龚光鲁，钱敏平．应用随机过程教程及算法和智能计算中的随机模型［M］．北京:清华大学出版社，2004

［4］吴晓敏．随机变量中马氏链的常返与强常返［J］．重庆工商大学学报:自然科学版，2011，28(4)343-346

［5］龚光鲁，钱敏平．应用随机过程教程及算法和智能计算中的随机模型［M］．北京:清华大学出版社，2004

An Improved Genetic Annealing Algorithm and Its Convergence Analysis

GAO Fa-ling
(Qindao College，Qingdao Institute of Technology，Shandong Qingdao 266100，China)

Under the constraint condition of nonlinear mixed integer programming model with 0-1 variable and integer variable，the solution to an improved genetic annealing algorithm is given，the corresponding Markov Chain is set up and its convergence is theoretically proved．

genetic annealing;Markov chain;traversal;convergence

O221．2

A

1672－058X(2015)02－0049－05

10．16055/j．issn．1672－058X．2015．0002．010

责任编辑:田 静

2014－06－15;

2014－09－10．

高发玲(1982-)女，山东青岛人，讲师，硕士，从事网络优化设计研究．