意料之外，情理之中——勾股定理之外的智慧“生成”

☉南京师范大学附属中学树人学校 王玉琴

意料之外，情理之中
——勾股定理之外的智慧“生成”

☉南京师范大学附属中学树人学校 王玉琴

每个学生都是鲜活灵动的智慧生命个体，并非是按照预设程序机械运动的机器，因而随机生成的“意外”是课堂上常见的现象.有些意外的生成能够带来丰硕的成果，教师如果善用教学智慧，实现师生、生生之间智慧的碰撞，那么很多课堂将演化成师生的一段智慧生命的精神之旅.正如苏霍姆林斯基说：“教育的技巧并不在于能预见到课堂的细枝末节，而在于根据当时的具体情况，巧妙地在学生不知不觉中做出相应的变动.”但意料之外的智慧生成，也并非完全出于偶然，正如灵感的出现，也是基于学习或研究者一定的知识基础和对问题的深入思索，而且，由于教学时间的限制，我们不可能对所有课都任由学生自由探索，一个智慧课堂，应更多地探讨适合学生知识、能力基础和学习方式、心理特点的有价值的问题.这就需要我们对一些典型的智慧生成教学案例，做必要的反思、探究，以便在有限的教学时空内，更多地激发学生潜在的智慧和求知热情.

一、课堂简录

笔者平时上两个班的课，在进行勾股定理新授课教学时，其中一个班的课上出现了一个意外提问.

生1：老师，那么非直角三角形的三边的平方具有什么关系？

当时笔者听了之后再想是继续本节课的教学内容还是解决该生的问题？在笔者任教的两个班中，这个班的同学基础好、能力强，平时就有许多同学喜欢钻研数学问题，也常有不少小发现，而且这位同学提出的问题是刚学的勾股定理的自然拓展，也是思维触角的自然延伸，从方法、思维上均有贯通之处，既有进一步研究的基础和价值，又比较适合这个班的学情，相信他们中多数人有能力探究这个问题，这对鼓励他们的探究热情、激活他们的思维、巩固所学的知识均有益处，显然比课后做几道勾股定理的应用题更有意义.瞬间犹豫后，笔者决定把时间让给学生，让他们在操作、思考中，展现、张扬个体生命中的智慧.如果一个个鲜活灵动而富有个性的智慧生命被完全禁锢在教师事先给定的框架中，这既是教育的悲哀，也是对智慧的漠视.

师：这个问题问得非常好！请同学们分学习小组讨论，看哪个小组能帮助他解决这个问题.

这下课堂炸开了锅，讨论氛围之热烈超乎笔者的想象，立刻便有人跃跃欲试.

生2：老师，∠C还是最大角吗？

师：好，为了表达方便，我们不妨规定钝角△ABC中，a≤b≤c.

生3：构造以a、b为直角边的直角三角形，如图1，过顶点C作CD⊥AC，同时取CD=CB=a（这里不够严谨，但容易说明点D在△ABC外——笔者注），在Rt△ACD中，a2+ b2=AD2，而∠ADB＞∠CDB=∠CBD＞∠ABD，所以AB＞AD，即a2+b2＜AB2=c2.（证法1）

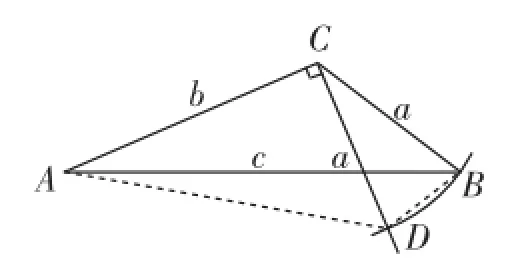
图1

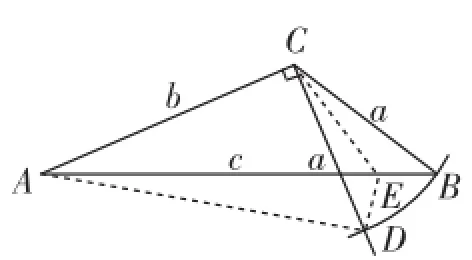
图2

生3刚说完，生4迫不及待地举起了手.

生4：老师，c＞AD还可这样说理：如图2，作∠DCB的平分线CE，交AB于点E，连接ED，可得△DCE≌△BCE，于是有ED=EB，而AE+ED＞AD，所以c＞AD.（证法2）

师：很棒！上面的证法构造了以a、b为直角边的直角三角形，运用勾股定理得到直角三角形的三边平方关系，然后再将这个直角三角形的斜边AD与钝角三角形的最长边c做比较，最终得出结论.还可以构造怎样的直角三角形呢？

生5：还可构造以c为斜边的直角三角形，如图3（严格说来，易证点E在△ABC外），由于∠ACE与∠BCE均为钝角，即为三角形中的最大角，所以有AE＞AC，BE＞BC，而AE2+BE2=AB2，所以a2+b2＜AB2=c2.（证法3）

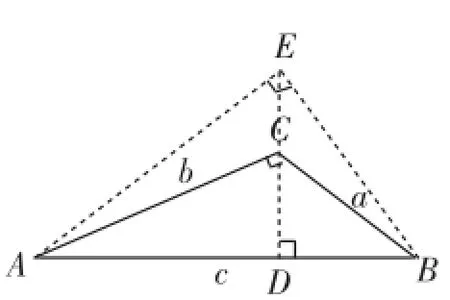
图3

师：简洁明了，非常漂亮！可见，欲求钝角三角形的三边平方关系，可将钝角三角形问题转化为与它相关的直角三角形问题.至于怎样转化，怎样构造直角三角形，方法可以是多种多样的，大家再试试.

生6：也可以过点B作高线，如图4，过点B作BE⊥AC交AC的延长线于点E，由勾股定理有x2+y2=a2，（x+b）2+y2= c2，将两式相减得c2-a2=2xb+ b2，所以a2+b2＜c2.（证法4）

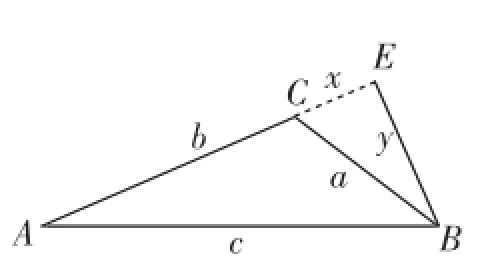
图4

师：好！通过作高BE，化斜为直，构造了两个直角三角形：△BEC，△BEA.以上几种证法的思路，都是构造直角三角形进行转化，借助于勾股定理的结论解决问题.想一想，从勾股定理的学习过程中我们还能得到什么启发，还可以找到其他的证明思路吗？

生7：老师，老师，还可以用图形的面积来解决！

师：太好了！这是证明勾股定理的主要方法，学习一个定理，我们不仅要知道它的结论和应用，还要理解证明的过程和方法，并学会将方法用于解决其他问题.生7，请把你的面积方法说给大家听听.

生7：将△ABC绕着点C逆时针旋转90°得到△A′B′C，如图5，连接AA′、A′B、BB′、B′A，因为四边形AA′BB′的面积为AB· A′B′=c2，同时它又等于△BCB′、△ACA′、△BCA′、△ACB′的面积和，所以所以（.证法5）

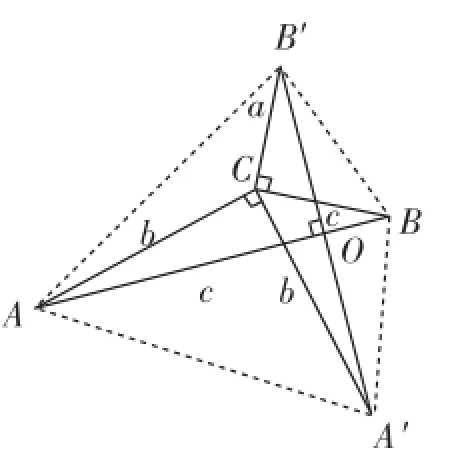
图5

学生7发现如此精巧的证明方法，赢得了大家的喝彩.这时课堂研讨气氛之热烈，学生思维之活跃，兴趣之浓厚，让笔者感慨万分.此法一经说出似乎平易，实为天资聪明的学生灵机一动闪出的智慧火花，多数学生不易想到.

此时，同学们和笔者的脸上都洋溢着收获的喜悦，下课的铃声在不知不觉中已悄然响起，可同学们还意犹未尽.掌声也在不经意中再次骤然响起，这或许是同学们此时心态的最好呈现.

图6

二、感悟与反思

这堂课大大超出了笔者的预设，但这样的意外却带来了精彩的智慧生成，不能不反思，自己在课堂上幸运地占有了如此丰富的教学资源（优秀的学生群体，学生的思维、创新方法的多样性，还包括学生自然生成的有价值的提问等），却差点扼杀了学生的思维，错过使学生享受探求知识过程的乐趣和摘到智慧果实的良机.因此，有必要以此为契机，深入探讨数学课堂智慧生成的特征和条件.

成尚荣教授曾指出：“智慧是一种整体品质，它在情境中诞生和表现，以美德和创造为方向，以能力为核心，以敏感和顿悟为特征，以机智为主要表现形式，科学素养与人文素养的结合赋予它底蕴和张力.”

数学课堂的智慧生成，是在数学思维的激发态、数学思想火花的灵光乍现中孕育迸发的.

反思这节课上学生的精彩生成，可以发现处于思维激发态的智慧具有以下一些特征，从中也许我们可以悟出一些数学教学的“真经”.

（一）智慧生成的特征

1.借力借法，变形变通

智者不以一己之力蛮干，而善于借助已有成果、方法，或借助于他人的思维、力量进行碰撞、交流；若问题不具备条件，则善于改造、变通，将其转化为已经解决的问题.这种转化化归的思想，在数学解题中屡见不鲜.例如证法1～4，将钝角三角形中边的平方关系问题通过构造、分解图形的方法，转化为直角三角形问题，从而运用勾股定理获证.

2.思维灵动，动静相生

思维灵动而充满创造性，是智慧课堂的重要特征.几何学研究运动变化中的不变性，新课程几何引入旋转、平移、对称、相似等变换，借助它们进行线段、角、区域的恒等、放缩转换，使图形成为动态的，在分分合合、运动变化中我们抓住不变性（量），给创造带来更多的空间和灵性.本课的多种证法中，不乏对称、等积变换的身影.

3.大胆想象，不离本质

证法1中，可以把角C想象成一把开合自如的剪刀，着张角C的减小，剪刀开口两个尖端的距离也在缩小.股定理的面积法证明，其本质是构造图形，使其面积含有与三边a，b，c平方有关的量，其中多数证法是构造正方形、直角三角形、梯形等规则图形.证法5却大胆想象，构造了一个不规则四边形.

4.整体感悟，直觉把握

智慧往往表现为对事物的宏观的把握，或一种穿越细节和逻辑链条的直觉、顿悟，如证法3，学生可以从整体上感悟到当角C为钝角时，所对的边c相对于a、b比角C为直角时要大些，因而直觉上感到可与角C为直角时相应的勾股定理的结论联系起来.当学生7兴奋地说：“老师，老师，还可以用图形的面积来解决！”这时他很可能是由于顿悟而惊喜.

5.整合迁移，融会贯通

智慧常生成于知识交汇处，这里是思想碰撞、知识联系的沃土，也是创造的源泉之一.如证法5，将面积法和变换法结合起来，显得新颖别致.智慧也常生成于知识、方法的迁移、类比，如鲁班从叶子的锐利类比联想，发明了锯子.证法6正是从勾股定理的欧几里得证法，加以巧妙迁移而得.

（二）智慧生成的条件

本节课上，学生的智慧火花迸发，处于思如涌泉的激发态，我们不妨冷静地进行理性反思：为何这个问题能产生如此丰富的结果？除了学生的良好素质、教师的热情鼓励与适时点拨、平时探究能力和创新意识的培养以外，问题的提出、知识的储备、方法的掌握、能力的培养等，也为智慧的生成打下了基础.细思之，本课的智慧生成，既是意料之外，也在情理之中.

综上所述，把握智慧课堂的特点，了解智慧孕育的条件，可以更好地抓住课堂上稍纵即逝的意外契机，及时促进智慧的生成，有意识地营造智慧的课堂.

1.马夫.初中数学教学策略［M］.北京：北京师范大学出版社，2010.

2.黄建平.通过巧设桥梁来提升学生的数学说题能力［J］.中学数学（下），2014（9）.W