确立条件优先之策略合理规划运算之思路——以二次根式计算（化简）为例

☉江苏省张家港市梁丰初级中学 邵美琴

确立条件优先之策略合理规划运算之思路
——以二次根式计算（化简）为例

☉江苏省张家港市梁丰初级中学 邵美琴

在二次根式的教学中，无论是二次根式的计算，还是二次根式的化简，学生都十分容易出现运算方面的错误.究其原因：一方面是学生对基本概念掌握不牢，对基本法则掌握不透，易发生这样或那样的错误；另一方面是二次根式的计算（化简）中，常常会涉及有理数的计算、整式的乘法和分式的化简等知识，有的学生这方面的知识本身比较薄弱，综合运用数学知识的能力不够，有些二次根式中含有较多的字母，而且这些字母大多数情况下是有限制条件的或者隐含着条件，学生在计算（化简）时经常会忽略这些条件，出现各种各样让人意想不到的错误.针对上述情况，在我们平时的课堂教学中，首先，要把二次根式的基本概念、基本法则讲清楚、讲透彻，特别要注重基础性问题的训练，使得学生对基础知识、基本技能达到熟练掌握的程度；其次，要培养学生理性审题的习惯，学会认真分析二次根式中所含式子（数据）的形式、隐含的条件，确立条件优先、运算其次的意识，在计算的过程中，要不断进行方法的比较，让学生掌握运算的要领、规律以及注意事项，使得方法不断优化，思维更加完善.下面结合笔者课堂教学的实例，进行一些简单的分析，以期对读者有一定的启迪.

一、“数据”处理优先，运用法则其次，让计算过程顺畅、自然

在二次根式的计算中，有些问题常常会涉及比较复杂的数据，如果直接使用法则忙于把每个式子作计算，因步骤繁多，难免会出现运算错误.因此，我们应先把相关的数据进行处理，通常的做法是将小数化为分数，将带分数化为假分数.这样处理后再应用法则，就能一鼓作气进行约分等计算，使得计算的过程顺畅、自然，提高运算的速度与正确率.

点评：鲁迅说，世间最不行的是读书者，较好的是思考者，更好的是观察者，他是用自己的眼睛去读世间的这部书.我们解题时也一样，首先要学会观察、分析，然后多角度、多维度地思考，寻求不同的解题思路，通过尝试、比较，选择最佳的解题方案.有意识地加强这方面的训练，学生的思维会更加完善，解决问题的方式才会变得更为灵活.

二、“式子”观察优先，应用性质其次，让条件变得简约、明晰

在二次根式的化简中，有些问题的题设条件较少，常常需要我们优先观察、整理式子，从基本概念出发，弄清条件与概念之间的有机联系，为解题思路的确立做好铺垫.著名数学教育家波利亚曾说：“回到定义中去”.此时，我们的解题世界常常会别有洞天.

此时，x+1＞0，x-2≤0，因此，|x+1|-|x-2|=x+1-（2-x）= 2x-1.

解法2：观察方程两边的特征，可知｛x≥0，解得2-x≥0，0≤x≤2.

以下同解法1.

点评：解法1关注左边的被开方数可以通过因式分解整理化简，再利用绝对值及二次根式的定义找到解题的突破口，让条件变得简约、明晰，应用起来也顺理成章；解法2回到了定义，回归到了基础，由二次根式的定义可得到“二次根式的双非负性”，即：①中，a≥0；②≥0，利用这一性质解题是我们常用的方法之一，在二次根式的教学中，应当予以加强.

所求实数m的值为0、1、3.

点评：求解含参数的方程的整数解是初中数学竞赛中最常见的题型，利用“二次根式的双非负性”确定上述方程实数根的取值范围是解决本题的关键，而分类讨论则是解决方程整数解问题最常用、最有效的方法.问题的解决足以说明：知识经验是解题的基础，联想转化是解题的关键，良好的认知建构是解决问题的保障.

三、确定字母范围优先，根式化简其次，让恒等变形有依据、有目标

数学家克莱因说过：“数学是人类最高超的智力成就，也是心灵最独特的创作，音乐能激发或抚慰情怀，绘画使人赏心悦目，诗歌能动人心弦，哲学使人获得智慧，科学可改善物质生活，但数学能给予以上一切.”面对相同的式子，不同的人会有不同的解决之道，而有时字母范围的优先确定，会让我们少走许多弯路、错道，让恒等变形的过程变得科学、合理.

解法2：同解法1得x＜0.

点评：学生在解答本题时，往往不考虑x、y的取值范围，误认为它们都是正数，不挖掘x的隐含范围，急于求成，造成各种各样的错误.因此，不管是解法1还是解法2，都必须优先确定字母x的取值范围，才可能获得正确的结果.解法1注重通性通法，利用了分母有理化和绝对值的概念，由“内”而“外”、有条不紊地进行化简；解法2“里”应“外”合，出奇制胜，把非负数-x看作一个整体，由“外”向“内”进行合理的运算，解法也相当简洁，让学生充分体会了逆向思维的独特性.同时告诉学生，在运用二次根式的性质解题时，既要注重性质成立的条件，又要学会性质的“正用”与“逆用”.特别地，将字母因式从根式“内”移到根式“外”或从根式“外”移到根式“内”，都必须考虑字母因式隐含的条件.

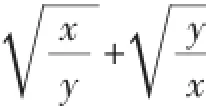
的值.

解：由题意知x+y＜0，xy＞0，所以x＜0，y＜0.

四、等价转化条件优先，代入演算其次，让条件与结论之间有桥梁、有衔接

著名的数学家、莫斯科大学教授C.A.雅洁卡娅曾在一次向数学奥林匹克参赛者发表《什么叫解题》的演讲时提出：“解题就是把要解的题转化为已经解过的题”.在二次根式的计算中，很多问题的条件是以无理式给出的，它与结论之间的联系并不十分明显，直接应用往往需要经过比较烦琐的运算过程，解题的正确率会降低.因此，在平时教学中，我们应当引导学生仔细审题，静心观察，学会等价转化条件，构建条件与结论之间的桥梁.

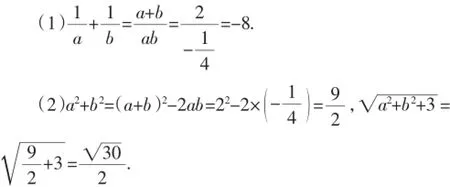
点评：通过观察数的特征，顺利地构造了对称式这种整体，把烦琐的无理数转化为有理数，这是快速解决本题的关键，也是提高解题正确率的有效途径.需要注意的是：在数学操作中实施等价转化时，我们要遵循熟悉化、简单化、直观化、标准化的原则，即把我们遇到的问题，通过转化变成我们比较熟悉的问题来处理，数学的解题过程，就是从未知走向已知、从复杂过渡到简单的化归转换过程.

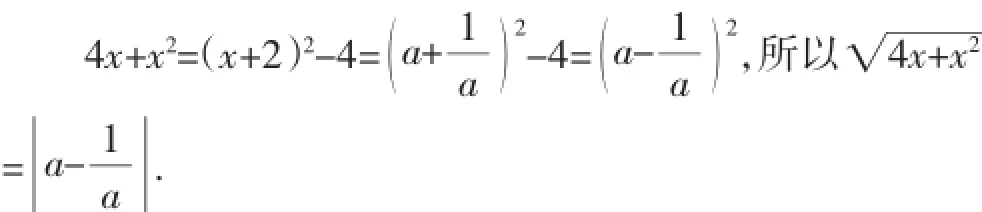
点评：布鲁纳指出：掌握数学思想方法可以使数学更容易理解和记忆，更重要的是：领会数学思想方法是通向迁移大道的“光明之路”.本例通过对条件等式两边平方，把无理方程转化为大家熟悉的有理方程，视x+2为一个整体，让条件与结论之间有了很好的衔接，使得解答过程巧妙、简捷.

初中数学教学中，提高学生的运算能力是贯彻始终的一项任务，一方面教师备课时要钻研教材，研究学生，精选例题与习题，上课时要讲清、讲透，示范到位，有效训练；另一方面要加强师生之间的交流与沟通，用爱心唤起他们对教师和数学的兴趣，及对自己学习数学的信心，切实提高运算的正确率.最后，我们还应当注意以下两个问题：一个是防止学生运算错误的发生，一个是学生产生了错误怎样去纠正它，这两者是互相联系的，两者相比，“防”重于“治”.在二次根式的教学中，我们更应该做好这些基础性的工作.WG