基于非线性海床刚度模型的钢悬链线立管动力响应分析
2015-05-24白兴兰黄维平谢永和赵春慧
白兴兰,黄维平,谢永和,赵春慧
(1.浙江海洋学院船舶与海洋工程学院,浙江舟山 316022;2.浙江省近海海洋工程技术重点实验室,浙江舟山 316022;3.中国海洋大学山东省海洋工程重点实验室,山东青岛 266100)
基于非线性海床刚度模型的钢悬链线立管动力响应分析
白兴兰1,2,黄维平3,谢永和1,赵春慧1
(1.浙江海洋学院船舶与海洋工程学院,浙江舟山 316022;2.浙江省近海海洋工程技术重点实验室,浙江舟山 316022;3.中国海洋大学山东省海洋工程重点实验室,山东青岛 266100)
基于P-y曲线模拟钢悬链线立管(SCR)-海床相互作用的力学行为,运用弹性地基梁模拟SCR流线段,研究海床刚度模型对SCR动力响应的影响。立管与海床的相互作用取决于土刚度、立管特性和沟槽的发展等诸多因素。现在的方法大多是将海床模拟为线性或非线性弹簧系统,而没有考虑土的塑性变形和吸力效应。运用P-y曲线模拟管-土相互作用过程,内容包括:①在浮体升沉运动和波浪载荷作用下,得到了管-土作用的荷载位移曲线、贯入深度和海床分布力的变化情况;②分析立管触地点的位移、弯矩、应力等动力响应特征,与线弹性海床模型进行了比较。研究表明,非线性海床土刚度模型较为准确地模拟了土的塑性变形和约束力对立管触地区动力响应的影响,弹性地基梁单元较好地模拟了立管的流线段,荷载位移曲线也体现了土吸力的产生和释放过程。
钢悬链线立管;立管-海床相互作用;非线性;弹性地基梁单元;海床吸力
随着海底能源开发不断向深海发展,半潜式、SPAR、TLP、FPSO等浮式平台成为油气开采的主力军,钢悬链线立管(Steel Catenary Riser,SCR)以其较好的适应性和低廉的造价越来越受到海洋石油企业的青睐,成为深水油气田开发的首选立管形式。SCR流线段与海床的相互作用是其独有特点,将会引起触地区较大的弯曲应力而引发疲劳破坏;深海立管的另一个热点问题是涡激振动,国内学者也围绕该问题建立了可靠的数学模型[1]和预报方法[2]。本文主要围绕管土相互作用展开研究,建立更符合工程实际的管-土接触模型。
由于SCR触地区与海床接触时的力学特性复杂,围绕该研究各国学者展开了大量模型试验和数值模拟研究。试验研究[3-7]表明:在浮体运动和波流作用下,特别是浮体的升沉运动,将会在海床形成最大深度为4倍~5倍管径的沟槽,土刚度有退化现象,软粘土海床有明显的吸力作用。Bridge等[3]通过拟合试验数据,得到海床法向约束力P与立管嵌入深度y之间的P-y关系曲线,如图1所示,其作用过程可分为初始嵌入、全接触、管土分离、重复嵌入四个阶段,即加载-卸载-重复加载的循环过程。

图1 海床土约束力模型[3]Fig.1 Model of seabed restriction to flowline
该试验模型为开展SCR触地区的数值模拟提供了重要参考。如Aubeny等[8]指出沟槽形成和管土相互作用过程,运用简化的P-y曲线来模拟管土作用;Elosta等[9]运用Orcaflex研究了海床土对立管触地区的垂向埋置和横向运动,分别应用非线性滞回曲线和双线性、三线性模型来模拟管土相互作用的竖向反力、切向摩擦力、沟槽侧向阻力作用,得到海床土刚度和立管的埋置深度;Wang等[10]将管土相互作用的滞回曲线进行线性化处理,运用ABAQUS触地单元来模拟立管-海床的作用,研究了海床土剪切强度和吸力因子对立管触地点动力响应和疲劳寿命的影响。Nakhaee等[11]考虑海床刚度衰减效应,运用P-y曲线模拟管土作用,通过数值模拟研究海底沟槽的发展和浮体周期运动对立管触地区弯矩的影响。Hodjat[12]基于ABAQUS研究了非线性海床刚度模型作用下,在不同吸力因子、不同土剪切强度下立管疲劳寿命的变化趋势。黄维平等[13-14]采用弹性地基梁模型模拟海床对立管的作用,并考虑吸力作用改进CABLE3D,与Orcaflex的计算结果吻合较好,验证了该程序的正确性。杜金新等[15]将P-y曲线进行线性化处理,将海床对立管的作用模拟为线性弹簧支撑;傅俊杰等[16]利用非线性弹簧单元模拟海床作用力,并考虑沟槽的侧向阻力,对立管触地区域进行动力响应分析;王坤鹏等[17]运用ABAQUS建立触地单元,将立管-海床的作用简化为线性、线性截断、线性截断并考虑海床吸力和刚度衰减模型3种模型,采用Euler梁四阶微分方程来求解海床对立管的作用力,将浮体的升沉运动作为激励条件,对立管触地点动态响应进行了分析。
上述研究大多运用接触单元或弹簧模型或触地单元来模拟立管-海床的作用,都在一定程度上对海床刚度模型进行了简化,没有完全真实地考虑海床的非线性作用。如Orcaflex中将立管模拟为线(Line)单元,通过无质量弹簧连接一系列集中质量节点,线单元的特性被集中于节点处,计算结果对单元长度的划分较为敏感;而弹簧模型则不能较好地模拟海床的吸力作用;ABAQUS采用Euler梁单元模拟,没有考虑立管的大挠度影响,将立管与海床的接触模拟为触地单元。
SCR动力分析程序CABEL3D基于大挠度柔性索理论,采用具有弯曲刚度的大挠度曲线梁模型来模拟SCR的悬垂段[18-19],弹性地基梁模型模拟SCR的流线段,将海床作用力作为分布力处理,对求解SCR的动力学问题具有较好的鲁棒性和有效性。考虑海床土的真实特性,基于P-y曲线建立法向滞回非线性管-土相互作用模型,通过迭代方法求解海床土非线性刚度,改进原程序中的线性海床刚度模型,得到新的程序CABLE3D RSI,研究表明:触地点处土约束力与位移的P-y曲线与试验模型吻合较好,体现了管土相互作用过程和土约束力变化情况;触地区形成“勺子”型沟槽,且深度逐渐增加,符合实际状态;海床刚度模型对立管触地点的竖向位移与应力特别是弯曲应力的动力响应有较大影响。
1 滞回非线性海床刚度模型
1.1 典型P-y曲线
文献[20]给出了典型的P-y曲线表达土体约束力与嵌入深度的函数关系,主要影响参数包括管径、立管接触单元的运动、土抗剪强度和吸力因子等,它们之间的函数关系用骨干曲线和双曲线来表达,包括试验得到的一些经验参数,立管初始贯入时符合骨干曲线,表达式为指数公式[18]:
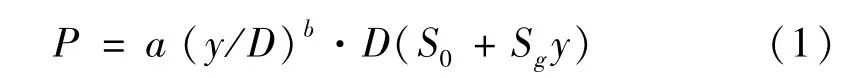
式中:P为立管单位长度的土约束力;S0为海床表面的剪切强度;Sg为剪切强度梯度;D为立管外直径;幂函数系数a,b与管土接触边界的粗糙度和相对埋置深度有关,由实验可以得到,a,b的具体值见表1。
P-y曲线的边界线可通过文献[11]提供的经验公式确定。通过编写子程序嵌入动力分析程序,运用改进程序计算某一工况下管土相互作用的P-y曲线,来验证程序的正确性。假设立管直径为0.203 2,自重为108 kg/m,S0=800 Pa,Sg=0 Pa/m,管土接触表面为粗糙,吸力因子fsuc=0.203,ψ=0.661,ω=0.433时,运用改进程序CABLE3D RSI得到P-y边界曲线,如图2所示,点1、2、3是曲线的关键点,控制着曲线的形状。该曲线符合典型P-y曲线所包含管土作用全过程:初始嵌入、全接触回弹、吸力作用和重新嵌入土中,与图1所示的试验模型类似。

表1 幂函数参数Tab.1 Power law coefficients
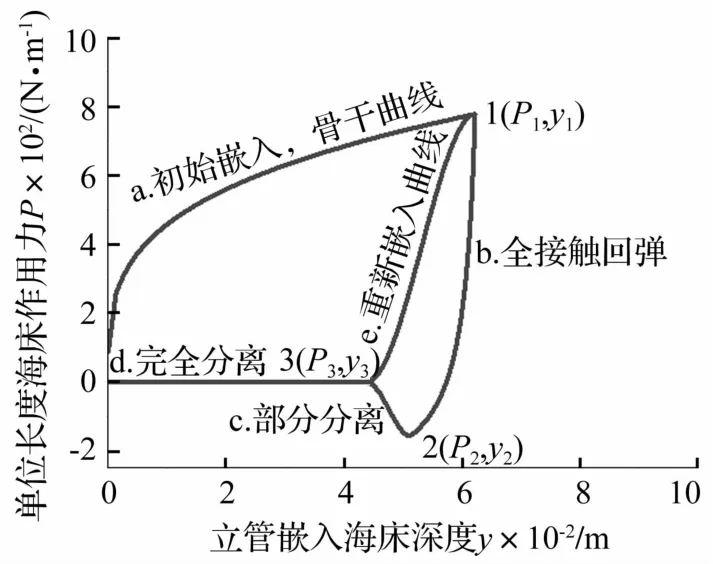
图2 典型P-y曲线Fig.2 A typical P-y curve
图2所示的边界曲线上任意一点(yrB,PrB),都有可能发生逆转,即加载(1-2)~卸载(3-1)之间的逆转,都遵循从逆转点开始的双曲线路径:

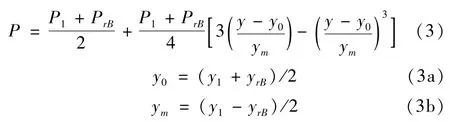
立管在同一嵌入深度y处,由于立管的运动方向不同,作用力方向也将不同,这是传统的弹簧单元无法模拟的。
1.2 弹性地基梁单元
立管的初始嵌入过程可以看作是梁与弹性地基的
式中,χ为方向系数,加载时χ=1,卸载时χ=-1。k0是S0有关的参数,k0=660×S0,ω是控制双曲线形状的参数。而当逆转点位于2-3区域,即吸力衰减时,则遵循三次曲线模式:作用,海床和立管的流线段连续接触,海床的约束力为连续分布力。与集中质量模型、弹簧支撑模型相比,计算结果更精确,速度更快。基于大挠度柔性索理论,立管流线段的弯曲振动方程表示为:
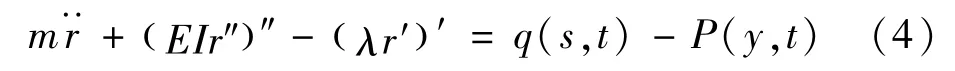
式中:m为单位长度质量;s为空间自变量,r是曲线坐标s和时间t的函数;EI为结构抗弯刚度;λ为Lagrange乘子,λ=T(s,t)-EIκ2(s,t),其中T(s,t)是截面的张力,对立管采用有效张力,κ(s,t)为立管的局部曲率,Euler直梁中则不包含此项;q为分布的外荷载,P为海床法向分布力,作为附加项加入运动方程:
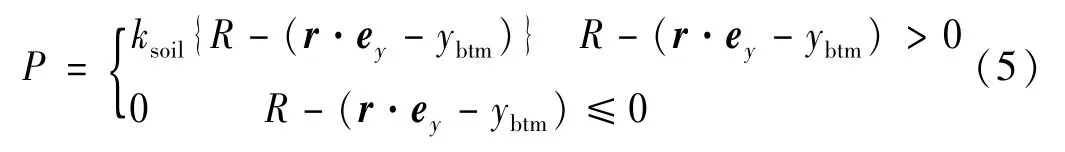
运用Galerkin方法将式(5)离散为一组常微分方程,将方程进行等效积分,其中海床法向约束力为:
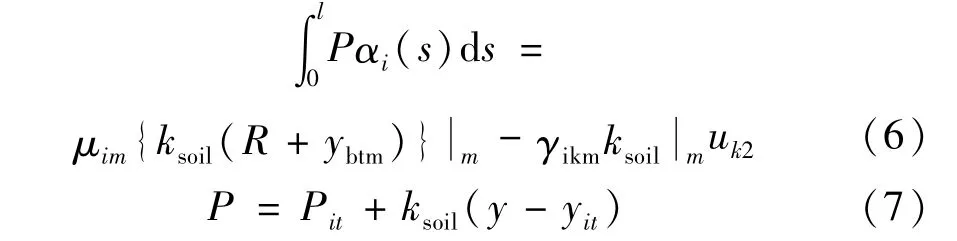
式中:l为单元长度,αi(s)为单元形函数;μim、γikm分别是[4,3]和[4,4,3]的形参数;ksoil为海床土刚度系数,可由海床法向分布力得到,对式(7)进行迭代求解,it是指迭代次数;ybtm为海床的竖向坐标;R为立管中心轴至最外层距离;uk2是单元节点竖向位移。对式(6)进行分部积分,可得一组常微分方程。其中单元形函数采用三次Hermite插值函数,节点位移为:

由于触地点处的单元和海床只有部分接触,则该处的竖向位移表示为:
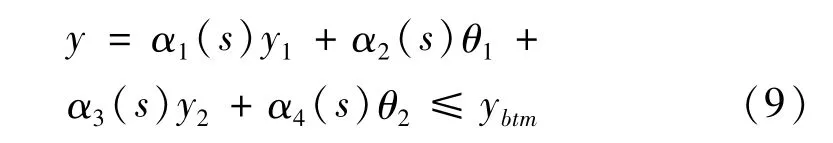
假设仅考虑立管平面内位移和转角位移,则式(9)可变换为:
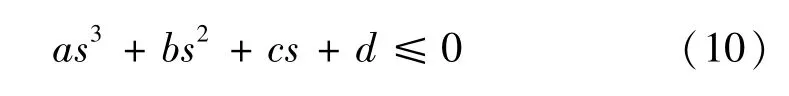
式中:
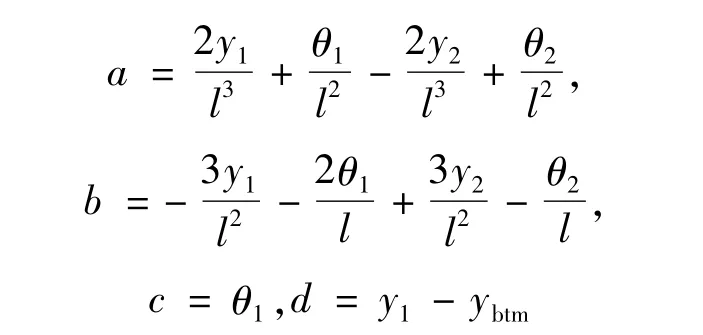
式(10)的解为触地点处单元和海床接触的部分,判断结构单元是否与海床接触是进行海床约束力计算的第一步。
管土作用效应可通过单元参数反映,如位移、速度、加速度等,这些单元参数在每一步增量中根据对应位置处节点的速度和竖向位移来确定,根据荷载-位移的关系可以得到海床土分布力,从而由式(7)通过迭代求解立管触地区不同位置的土刚度。
2 动力分析
2.1 动力分析程序CABLE3D RSI
CABLE3D是用来求解锚链/立管系统的动力学的有限元程序,采用非线性有限元方法将结构模拟为细长杆件。原程序中,将海床土对立管的约束力模拟为线性弹簧-阻尼系统,立管贯入海床的深度等于其半径,海床的线性刚度为立管的湿重S除以贯入深度R,即S/R。阻尼系数取临界阻尼系数为立管单位长度质量。可见海床的刚度和阻尼系数的选取都没有考虑海床土的特征类型。因此,本文拟采用非线性滞回P-y曲线模拟海床约束力,弹性地基梁模拟立管与海床的接触段,来改进弹性海床模型、直梁单元对立管与海床相互作用的模拟,改进程序命名为CABLE3D RSI,并应用该程序进行SCR的整体动力分析,可以更准确地预测立管与海床相互作用的力学行为和立管触地区的疲劳损伤。
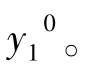
动态分析过程更加复杂,需要判断立管单元是否与海床接触、时间步与迭代次数的大小、加载-卸载过程等。迭代求解过程与静态分析类似,通过反力、刚度与位移的迭代求解,将运动方程和约束方程统一表达为矩阵aδx=b的形式,然后进行求解。其中每一时间步的每一次迭代都会得到新的位移值,对比前后两次迭代得到的位移值,如果能满足精度要求,则说明通过该位移值得到的海床土法向约束力和刚度,以及该法向约束力和刚度引起的立管位移是与确定这两个值时的位移是相同的。整个迭代过程中,充分考虑了海床刚度的非线性、管土的分离。
2.2 应力计算
根据DNV-RP-F204[10]中关于循环应力的计算,立管应力为轴向应力和弯曲应力的线性组合:

式中轴向应力σa和弯曲应力σm分别由立管的有效张力Teffect和弯矩M计算得到,弯矩M由式(12)计算得到:

式中r′,r″表示对曲线坐标s的一阶、二阶偏导,H为立管的截面扭矩,这里假设H=0。
2.3 SCR模型参数及海床土特性
选取SCR所在海域的水深为1 100 m,总长度为2 400 m,水平跨度为1 750 m,顶端为坐标原点,锚固点的坐标为(1 750,-1 100,0),起始角为15.2°,相关参数见表2。立管顶端通过柔性接头与浮式平台相连,忽略其转动刚度,仅考虑二维平动。假定在立管顶端施加周期升沉运动或纵荡运动,来模拟浮式结构的周期运动,本文选取升沉运动的周期为12 s,振幅为2 m。
对SCR来说,除了管土相互作用是影响立管疲劳的主要因素之外,还有VIV、安装荷载、流等载荷,鉴于主要考虑海床刚度模型对立管动力分析的影响,故仅考虑平台周期运动和线性波浪载荷,波高为1.25 m,波周期为5.3 s,不考虑其他环境载荷,对于管内外流体只考虑其质量。
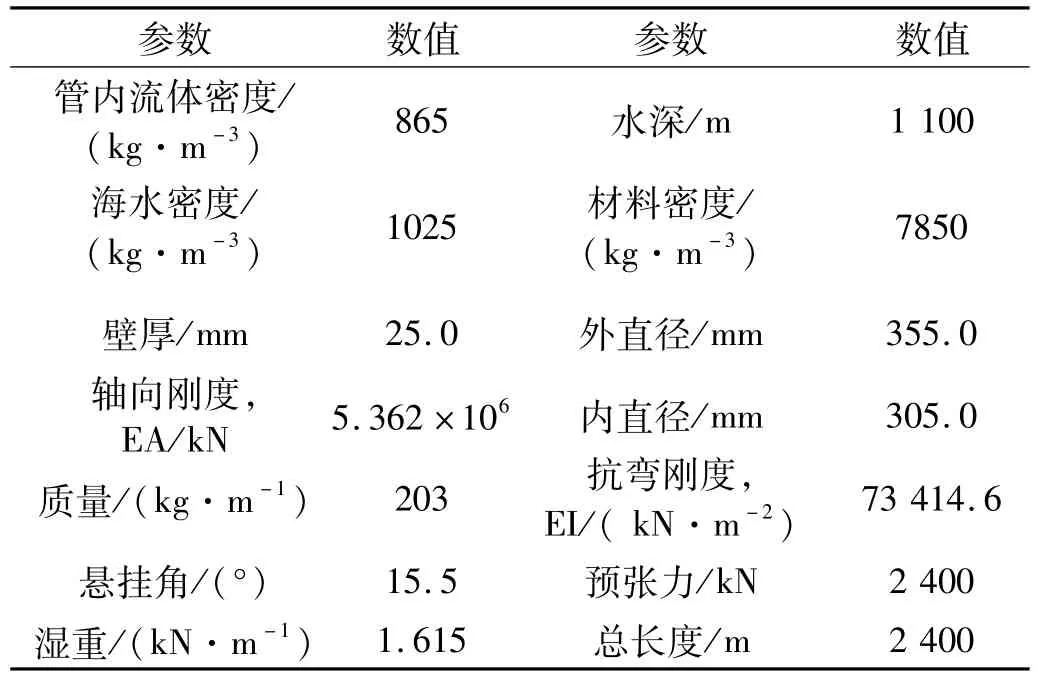
表2 SCR模型参数Tab.2 Parameters of the SCR

表3 非线性海床模型参数Tab.3 Hysteretic non-linear model parameters
通常情况下,软粘土海床表面的剪切强度S0的范围是1.2~3.8 kPa,剪切梯度Sg为0.8~2.0 kPa/m[4,7]。为了方便比较,本文选择低海床强度,经计算知该强度与采用的线弹性海床强度较为接近,具体参数见表3。
3 数值计算
对上述计算模型,用Galerkin方法对运动方程(10)进行离散,运用Newmark-β积分法求解单元方程,通过迭代得到土反力、立管位移和海床刚度等关键参量。立管全长划分400个单元,每个单元长度为6 m。
3.1 立管与海床相互作用动力响应
滞回非线性海床模型包括管土作用的不同阶段,有些节点会部分离开或完全离开海床,有些节点不会离开海床,在加载-卸载之间进行反转。图3所示为立管触地区节点位置示意图,给出了一些特殊点的位置,触地点为N239,节点N244为最大贯入深度对应的节点,而节点N252是触地区的另一个边界点。
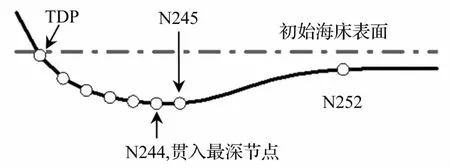
图3 SCR触地区节点位置示意图Fig.3 Schematic position of sample nodes in the TDZ
在立管顶端施加为周期12s、振幅为2m的升沉运动,海床土和立管特性见表2、表3。通过CBALE3D RSI计算,可得到贯入深度与海床分布力之间的关系曲线。图4所示为触地区节点N240、N244和N246的土反力位移曲线,横坐标表示立管的贯入深度,纵坐标为海床法向分布力,其中正值表示支撑力,负值表示吸力(由吸力因子确定)。节点N240经历了滞回曲线的整个过程包括初始嵌入即骨干曲线-全接触-部分分离-完全分离-再加载,且完全符合按照程序设定的P -y曲线路径。图4中还标出了第一、二次循环的特征点位置11、21、31和12、22、32。随着管土的往复作用,可以发现荷载位移曲线逐渐向右移动,说明随着时间推移,贯入深度在不断增加,当到达一定深度后,荷载位移曲线将会重复,贯入深度不再发生大的变化而趋于稳定,沟槽发展缓慢。
节点N244是贯入深度最大的点,也经历了P-y曲线的全部过程,但仅经历了骨干曲线的一部分,即土反力不是从0开始增加的。N246只经历了卸载-再加载过程,说明该节点处立管并没有与海床分离,从而没有受到海床土的吸力作用。这也说明触地区并不是所有的节点都会经历相同的管土相互作用过程,在某一时刻不同位置的节点将受到大小不同的海床约束力,经历不同的非线性管土相互作用过程。
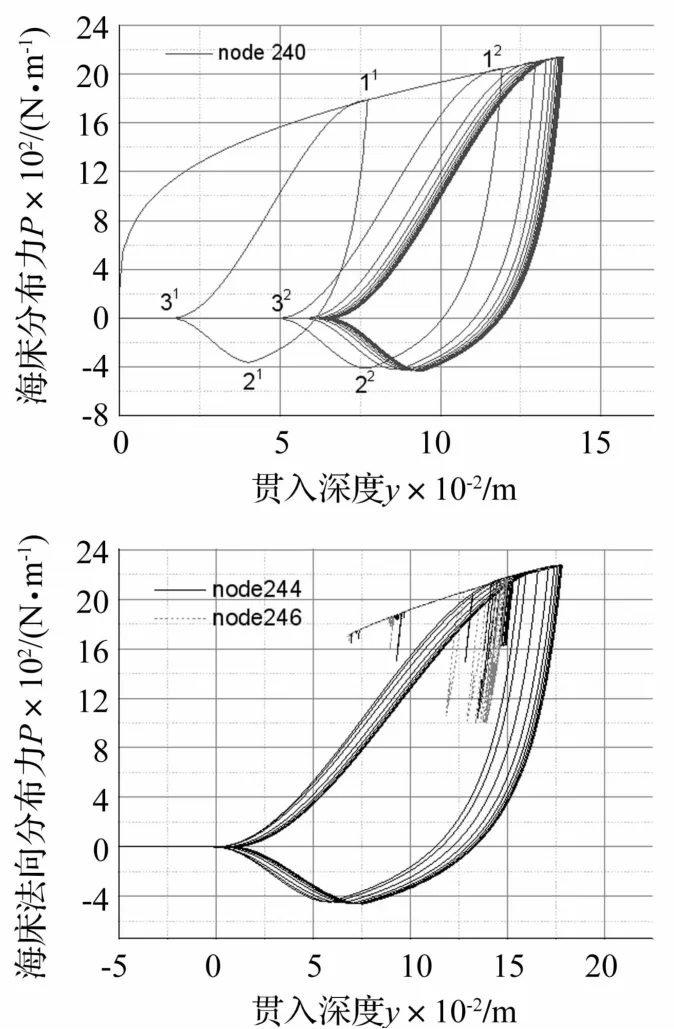
图4 非线性海床管-土作用动力响应曲线Fig.4 Riser-soil dynamic response at nodes 240,244,246

图5 循环荷载作用下贯入深度的发展Fig.5 Progressive penetration under cycle loading
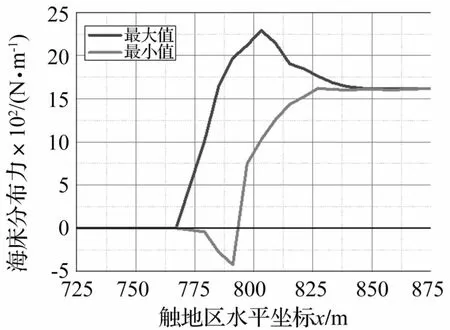
图6 循环荷载作用下海床分布力包络图Fig.6 Seabed resistance envelop with 10 cycles of load
图5、图6所示为在10个周期荷载作用下,立管在海床土的贯入深度逐渐发展示意图和海床分布力包络图,其中触地点和最大贯入点N244的位置在发生变化,沿着图5中的虚线变化,而进入流线段的单元节点N252的位置基本没有变化。从图5可以看出,立管贯入土中形成如勺子状的沟槽,随着循环载荷的次数增加,沟槽逐渐变深,特别是运动的初始阶段比较明显,运动稳定之后,沟槽深度增加缓慢。初始状态下,立管的贯入深度只有0.059 33 m,最大海床分布力为1 769 N/m,10个周期载荷之后,贯入深度达到了0.134 2 m,最大海床分布力为2 290 N/m,有很大程度的提高。相同工况下,相对于线弹性海床模型来说,得到的海床分布力为1 668.5 N/m,而对于刚性海床模型,海床分布力为26 980 N/m。图6中海床分布力的最小值是负值,即吸力,其值为-423.2 kN。由此可见,采用线弹性海床得到的海床分布力与低强度非线性海床较为接近,但是刚性海床分布力相对大很多,采用线弹性海床或刚性海床都与实际情况有较大差别,从而因管土作用力学模型的不准确而导致疲劳寿命预测的误差较大。
3.2 不同海床模型模拟结果比较
分别运用线弹性海床和本文的非线性海床刚度模型对SCR进行整体分析,得到立管触地点的动力响应,并将结果进行了对比。图7~图10分别给出了触地点N239的竖向位移、弯矩、有效张力和应力的时程曲线。可以看出:触地点竖向位移的运动幅度受海床刚度模型的影响较大,线弹性海床刚度模型没有考虑海床土的实际特性和吸力效应,因此运动幅度较大。
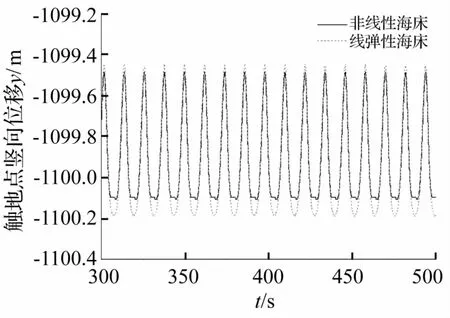
图7 N239节点处竖向位移的时程曲线Fig.7 Time history of vertical displacement at N239

图8 N239节点处弯矩时程曲线Fig.8 Time history of bendingmoment at N239
图8和图9是决定节点应力的弯矩和张力时程曲线,图10是轴向应力和弯曲应力线性组合之后的应力时程曲线对比。由图可知,有效张力时程曲线的趋势不受海床刚度模型的影响,但是非线性海床作用下触地点的弯矩和应力幅值明显增大,而且在峰值附近出现了许多小循环,而疲劳分析中通过雨流计数法提取循环应力幅值来确定其疲劳损伤,应力幅值对立管疲劳会产生较大影响。图10可见应力变化趋势与弯矩相似,可见触地点的应力主要由弯曲应力提供。因此说明,立管触地点发生疲劳破坏的主要因素是该处的峰值弯矩和循环应力。

图9 N239节点处有效张力时程曲线Fig.9 Time history of effective tension at N239
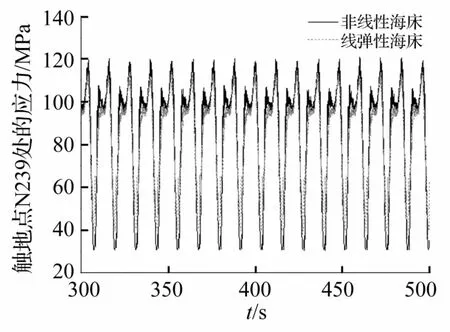
图10 N239节点处应力时程曲线Fig.10 Time history of stress at N239
4 结 论
基于P-y曲线建立了滞回非线性海床刚度模型,得到改进程序CABLE3D RSI,运用迭代法求解海床的实际刚度、海床约束力和贯入深度,得到管-土相互作用的荷载位移曲线;将立管的流线段模拟为弹性地基梁,相对于弹簧支撑模型来说,具有对单元划分长度不敏感、考虑吸力效应等优势,能够准确地模拟管土的相互作用;在浮体周期升沉运动和线性波浪载荷作用下立管与海床土的动态响应,包括荷载位移曲线、海床沟槽的形成以及竖向位移、弯矩等动力响应时程,得到了有价值的结论:
(1)在周期载荷作用下,海床约束力与贯入深度之间的荷载位移曲线,完全符合P-y曲线,并体现了海床土吸力的产生和释放过程,证明了程序的正确性;海底沟槽随着时间推移,会逐渐加深,运动稳定之后,沟槽的深度变化减慢;并给出了循环载荷作用下海床约束力包络图;
(2)动力响应时程曲线体现了非线性和线性海床模型对触地点区域的位移、弯矩和应力有较大影响,但对轴向应力影响不大。
[1]吴学敏,黄维平.考虑大变形的大柔性立管涡激振动模型[J].振动与冲击,2013,32(18):21-25.
WU Xue-min,HUANGWei-ping.A new model for prediction vortex-induced vibration of a long flexible riser with large deformation[J].Journal of Vibration and Shock,2013,32 (18):21-25.
[2]曲雪,薛鸿祥,唐文勇.深海顶张式立管顺流涡激振动响应预报方法[J].振动与冲击,2013,32(15):32-36.
QU Xue,XUE Hong-xiang,TANG Wen-yong.In-line VIV analysis of deep-water top tensioned riser[J].Journal of Vibration and Shock,2013,32(15):32-36.
[3]Bridge C,Willis N.Steel catenary risers-results and conclusions from large scale simulations of seabed interactions [C]//Proc,international conference on deep offshore technology,2002.
[4]Bridge C,Howells H,Toy N,Parke G,Woods R.Full scale model tests of a steel catenary riser[C]//Proc,international conference on fluid structure interaction,2003,36:107-116.
[5]Bridge C,Laver K,Clukey E,Evans T.Steel catenary riser touchdown point vertical interaction models[C]//Proc,offshore technology conference,2004,OTC16628.
[6]Willis N R T,West P T J.Interaction between deepwater catenary risers and a soft seabed:large scale sea trials[C]//Proc.offshore technology conference,2001,OTC 13113.
[7]Hodder M S,Byrne B W.3D experiments investigating the interaction of a model SCR with the seabed[J].Applied Ocean Research,2010,32:146-157.
[8]Aubeny C P,Biscontin G,Zhang Jun.Seafloor interaction with Steel Catenary Risers[R].Texas:Texas A&M University,2006.
[9]Elosta Hany,Huang Shan,Incecik Atilla.Dynamic response of steel catenary riser using a seabed interaction under random loads[J].Ocean Engineering,2013(69):34-43.
[10]Wang Kun-peng,Xue Hong-xiang,Tang Wen-yong,et al.Fatigue analysis of steel catenary riser at the touch-down point based on linear hysteretic riser-soil interaction model[J].Ocean Engineering,2013(68):102-111.
[11]Nakhaee A,Zhang J.Trenching effects on dynamic behavior of a steel catenary riser[J].Ocean Engineering,2010(37):277-288.
[12]Shiri H.Response of steel catenary riser on hysteretic nonlinear seabed[J].Applied Ocean Research,2014(44):20-28.
[13]黄维平,孟庆飞,白兴兰.钢悬链式立管与海床相互作用模拟方法研究[J].工程力学,2013,30(2):14-18.
HUANG Wei-ping,MENG Qing-fei,BAI Xing-lan.The simulation of the interaction between SCR and seabed[J].Engineering Mechanics,2013,30(2):14-18.
[14]孟庆飞,黄维平.钢悬链线立管与海底相互作用弹性基础梁模拟方法研究[J].海洋工程,2013,31(7):74-78.
MENG Qing-fei,HUANGWei-ping.Simulation of SCR and seabed with elastic foundation beam model[J].The Ocean Engineering,2013,31(7):74-78.
[15]杜金新,Low Y M.海洋立管-海床土体接触作用数值分析[J].工程地质计算机应用,2008(4):1-6.
DU Jin-xin,Low Y M.Numerical analysis of contact action between offshore riser and seabed[J].Computer Application of Engineering Geology,2008(4):1-6.
[16]傅俊杰,杨和振.深海钢悬链线立管触地点动力响应分析[J].海洋工程,2009,27(2):36-40.
FU Jun-jie,YANG He-zhen.Dynamic response analysis of a deepwater steel catenary riser at the touchdown point[J].The Ocean Engineering,2009,27(2):36-40.
[17]王坤鹏,薛鸿祥,唐文勇.基于海床吸力和刚度衰减模型的深海钢悬链线立管动力响应分析[J].上海交通大学学报,2011,45(4):585-589.
WANG Kun-peng,XUE Hong-xiang,TANG Wen-yong.Dynamic response analysis of deepwater steel catenary riser based on the seabed suction and stiffness degradation model [J].Journal of Shanghai Jiaotong University,2011,45(4):585-589.
[18]白兴兰.基于惯性耦合的深水钢悬链线立管非线性分析方法研究[D].青岛:中国海洋大学,2009.
[19]黄维平,白兴兰.深水钢悬链线立管的大挠度柔性索模拟方法[J].工程力学,2009,26(11):228-231.
HUANG Wei-ping,BAI Xing-lan.The simulation of steel catenary risers in deepwater with flexible cable model[J].Engineering Mechanics,2009,26(11):228-231.
[20]Jiao Ya-guang.Non-linear load-deflection models for seabed interaction with steel catenary risers[C]//Mater of science thesis in civil engineering.Texas A&M university,2007.
Dynam ic response analysis of steel catenary riser based on a nonlinear seabed stiffnessmodel
BAIXing-lan1,2,HUANGWei-ping3,XIE Yong-he1,ZHAO Chun-hui1
(1.School of Naval and Ocean Engineering,Zhejiang Ocean University,Zhoushan 316022,China;2.Key Laboratory of Offshore Engineering Technology of Zhejiang Province,Zhoushan 316022,China;3.Shandong Key Laboratory of Ocean Engineering,Ocean University of China,Qingdao 266100,China)
Here,the interaction behavior between SCR and seabed was simulated based on the P-y curve,the influence of a nonlinear seabed stiffnessmodel on the dynamic response of SCR was studied using an elastic foundation beam to simulate SCR flow line.Itwas shown that the riser-seabed interaction depends on several factors,such as,soil stiffness,riser characteristics,and development of trenches.In the currentmostmethods,the seabed was taken as a linear or nonlinear spring system not considering plastic deformation of soil and its suction effect.The P-y curve was used to simulate the relation between seabed resistance force and the vertical penetration of the riser into seabed during their interaction.The interaction between SCR and soil's hysteretic load-penetration curve,the depth of penetration and the envelop curve of seabed contributed force under cyclic heavemotion and linear wave were obtained.Time histories of the contact points between SCR and soil's vertical displacement,bending moment,effective tension and stresses were analyzed.The results using the nonlinear seabed model were compared with those using the linear seabed model.The results showed that the nonlinear seabed stiffnessmodel has a significant influence on the dynamic responses of SCR;the elastic foundation beam element simulates the SCR's flow line better,and the load-penetration curve reveals the genearation and release of suction.
steel catenary riser(SCR);riser-seabed interaction;nonlinear;elastic foundation beam element;seabed suction
TU311.3
A
10.13465/j.cnki.jvs.2015.21.015
浙江省自然科学基金项目(LZ15E090001,LY15D060005,LY14E090003)
2014-07-22 修改稿收到日期:2014-11-20
白兴兰女,博士后,副教授,1980年8月生
