一种改进的高度计风速反演模式函数研究

樊旭艳，顾艳镇，范开国

（1.海军海洋气象水文中心，北京100161；2.中国海洋大学 信息科学与工程学院，山东 青岛266100；3.香港中文大学 太空与地球信息科学研究所，香港999077；4.中国人民解放军91039部队，北京102401）

0 引言

高度计可用于海表面风速大小的测量。海面斜率分布是由海表面风速引起的。风速增加，海表面的均方斜率随之增加，使得雷达脉冲的侧向散射能量增加，从而导致高度计在垂直方向上接收的标准化雷达后向散射截面σ0下降。因此可以利用高度计测量的后向散射截面σ0获得海表面风速。虽然只能测量海面风速的大小，但在海洋学研究过程中具有特殊意义：（1）高度计可提供同步的风、浪数据；（2）高度计星下点风速空间分辨率高于散射计；（3）可以将高度计、散射计和微波辐射计测量的风速进行数据融合和数据同化［1］。

但在强风降雨的天气条件下，高度计不能准确反映海表面的风速情况［2－3］，导致高风速资料缺乏，因此以往提出的高度计风速反演模式函数只适用于风速小于20m／s的情况。本文利用气象预报模式的台风风速资料，开展高度计风速反演模式函数改进研究，得到1个适用于10～40m／s风速的反演模式函数，使高度计能更准确地反演高风速。

1 数据准备

1.1 卫星高度计资料

JPL（Jet Propulsion Laboratory）网站上提供了2002年至今Jason－1的沿轨道数据，其中有未做校正的Ku波段和c波段的σ0值，需要利用提供的大气偏差和仪器偏差做校正［4］。本文选用的是2002年到2006年Ku波段的σ0值。

1.2 高风速资料

WITTER和CHELTON［5］用气象预报模式证明风速概率密度函数的年际变化很小。YOUNG［6］论证了利用气象预报模式获得的台风风速用于高度计风速反演的可行性，并用HOLLAND算法反演的台风风速和Geosat的后向散射系数资料获得了1个可用于20～40m／s风速的海表面风速模式函数。HOLLAND 算法［7］为：

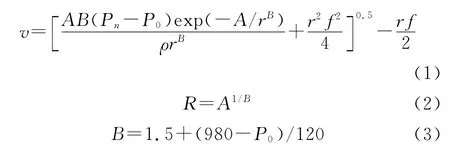
式中：v是距离台风中心为r处的梯度风速，f是台风中心所在纬度的科氏参数，R为最大风速半径，ρ为空气密度，P0是台风中心的气压值，Pn是台风边缘气压值，A和B 是决定台风尺度的两个参数。HOLLAND［7］将Pn取为无限远处的气压值，即认为台风半径无限大，台风的气压随着离中心距离的增大而增大。因此HOLLAND算法中使用的Pn值偏大，从而反演得到的风速值比实际值偏大。而且由式（1）可知，r越小，反演得到的值高估也越多。但在风速较小的区域，由于该算法忽略了背景天气的影响，因而低估了风速值［6］。

CARR和 ELSBERRY［8］也指出 HOLLAND 台风预报算法将台风扩展到无限远，导致由该算法获得的台风外围风速不准确，并提出了一个基于角动量守恒的台风风速反演算法。CARR和ELSBERRY已经证明了在半径小于400km范围内由角动量模式反演的台风风速与观测值是一致的［8］。YIN et al［9］将角动量模式计算得到的台风风速和Quicksat观测的台风风速作为风场数据输入RMOS模式，模拟台风经过时海表面叶绿素含量的变化，结果表明用Quicksat观测的台风风速作为风场数据模拟得到的叶绿素含量要比卫星测得的低，而用角动量模式计算得到的台风风速作为风场数据模拟得到的叶绿素含量与卫星测量值更吻合。这也说明了角动量模式反演的台风风速是准确的。

YIN et al［9］考虑到HOLLAND算法在台风外围区域不能准确反演台风风速，因此在台风外围区域采用角动量模式，而在台风内核区域采用Rankine模式反演台风风速。在台风最大风速半径以外区域的风速值由下式获得［8］：

式中：rm是台风的最大风速半径；r是计算点到台风中心的距离；f0是台风中心所在纬度的科氏参数；X是表征摩擦作用的参数；M是跟角动量相关的1个参数，可以由边界条件计算获得。台风的各个参数可在JTWC（Joint Typhoon Warning Center）网站上获得，包括：时间、位置、最大风速半径、最大风速和风速为17.5m／s时的半径。方程（4）的边界条件是：

式中：rv2是风速为17.5m／s时的半径，JTWC网站提供了在不同象限的rv2。

在台风最大风速半径以内区域的风速值由下式得到［7］：

式中：r是计算点到台风中心的距离，c1是一个常量，方程（7）的边界条件是式（5）。将所得海表面台风风速乘以一个系数0.8转化为海表面上10m处风速［10］。

JTWC网站（http：／／metocph.nmci.navy.mil／jtwc.html）提供了全球各个海域发生的台风的相关参数，为与Jason－1资料同步，本文选取了2002年到2006年的北太平洋资料，用于检验YIN台风风速反演算法的准确性，以及拟合和检验新的高度计风速反演模式函数。

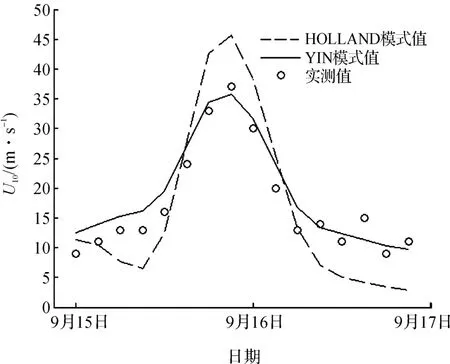
图1 风速结果对比图Fig.1 The comparison of wind speeds

图1给出了本文采用的YIN算法反演风速、HOLLAND算法反演风速和气象观测站实测风速的对比。图中，圆圈为气象观测站（24.33°N，124.17°E）观测的2006年第13号台风“珊珊”的风速，黑色实线是根据JTWC网站提供的台风“珊珊”的参数用YIN算法反演得到的风速，黑色虚线是根据JTWC网站提供的台风“珊珊”的参数用HOLLAND算法反演得到的风速。由图可以明显看出YIN算法反演的风速更接近观测值，而用HOLLAND算法反演的风速偏离实测值较大。这验证了前文提到的在高风速时HOLLAND算法反演的风速高于实测值，在低风速时反演值低于实测值的结论。

2 海表面风速反演模式函数

2.1 已提出的海表面风速反演模式函数

镜面反射理论表明，雷达后向散射截面（σ0）与海面均方斜率）之间存在下列关系［11］：

式中：ρ（0）代表在垂直入射条件下海－气界面的菲涅耳反射率，θ是雷达波束相对于海表面的入射角，α为校准因子。海表面的均方斜率是风速U10的函数［11］，因此雷达后向散射截面（σ0）也是风速U10的函数。简单地说，高度计测量的后向散射截面σ0和海表面风速之间存在着一种非线性反比关系。高度计测量的σ0必须通过模式函数才能转换成海表面风速。因此，模式函数的质量直接关系到海表面风速的反演精度。

迄今为止已提出大约20种高度计风速反演模式函数，其中比较著名的有 BROWN et al［12］、CHELTON 和 MCCABE［13］、CHELTON 和 WENTZ［14］、WITTER和CHELTON［5］等提出的仅依赖于Ku波段后向散射截面的单参数模式函数。其中WITTER和CHELTON提出的模式函数已经发展成为ERS－1，ERS－2和 T／P高度计的业务化风速反演算法［5］。但是这些模式函数在风速大于20m／s时会完全失效［15］。

GOURRION et al［16］通过对 TOPEX／Poseidon高度计资料与NSCAT风速数据进行时空匹配处理，得到同步数据集，利用人工神经网络方法试验得到反演海面风速［16］的两参数模式函数（后向散射截面和有效波高作为输入的参数）。该模式函数已作为Jason－1的2级b产品中风速业务化算法。但是GOURRION et al［16］的两参数模式函数在网络训练中使用的是散射计的风速资料，在强风情况下散射计严重低估海表面风速，导致该模式函数只适用于风速小于30m／s的情况。

YOUNG［6］通过对HOLLAND算法获得的台风风速和Geoset高度计观测的后向散射截面进行对比分析，给出了1个适用于20～40m／s风速的模式函数，即：

但是由于HOLLAND算法自身的缺陷，导致由HOLLAND算法获得的台风外围风速不准确，因而也影响了YOUNG函数的精度。

2.2 本文提出的海表面风速反演模式函数

本文用YIN算法反演台风风速值，通过对比卫星高度计观测的后向散射截面与同步的台风风速值给出了1个新的经验模式函数。在保证台风反演模式函数准确的前提下，台风的参数决定了反演得到的风速值的准确程度，为得到较准确的台风风速值，本文在所有台风资料中选取卫星高度计地面轨迹穿过台风中心的台风，同时舍去了参数有较大波动的、路径变化较快的台风［5］。表1列出了本研究选取的台风及各台风参数。

表1 本研究选取的台风及各台风参数Tab.1 Parameters and information of the typhoon selected in this study

由图2中4个台风（1～4号台风）所反演得到的 风速和高度计后向散射截面的散点图可以明显看出σ0和U10有很好的相关性，随着风速的增大，海面粗糙度会随之增加，雷达脉冲的侧向散射能量增加，后向散射能量减少，从而导致σ0减小。因此可用最小二乘法拟合得到σ0和U10的关系如下：

图2 本文提出的模式函数、Jason－1业务化模式函数和YOUNG模式函数对比及由4个台风反演得到的风速值Fig.2 The comparison among the model developed in this study，the operational method of Jason－1and YOUNG，and the wind speeds reversion from 4typhoons

在图2中对本文提出的模式函数、Jason－1业务化模式函数和YOUNG模式函数进行了对比，图中黄线为本文提出的模式函数，红线为本文模式函数的95%置信区间，绿色圈为Jason－1业务模式函数，蓝线为YOUNG模式函数。需要注意的是，金涛勇等［17］发现Jason－1高度计GDR数据产品的“b”版本数据的后向散射截面和T／P高度计数据产品的后向散射截面有2.5dB的偏差。LEFEVRE et al［18］为了将T／P测得的后向散射截面用于Geoset的高度计风速反演模式函数，给T／P测得的后向散射截面加上了－0.4dB的偏差。因此用YOUNG模式函数和Jason－1测得的后向散射截面反演风速时，要给Jaosn－1的后向散射截面加上－2.9dB的偏差。由图2可以看出，当U10＜27m／s时，本文的模式函数和Jason－1业务化模式函数结果基本相同，当U10＞27m／s时，Jason－1业务化模式函数明显已不再适用。相比本文模式函数和Jason－1业务化模式函数，YOUNG模式函数偏离较大，这是由于其所采用的HOLLAND台风风速反演算法将台风范围扩展到无限远而导致。因此本文模式函数能在整体上更好地体现σ0和U10的关系，更适合用于Jason－1高度计风速反演。

为进一步检验本文模式函数的准确度，将由3种高度计风速反演模式函数得到的风速分别和由台风风速反演算法得到的风速（台风资料采用5号和6号台风）作对比来判断各种模式函数的优劣，图3中红色圆圈为本文提出的模式函数，黑色圆圈为YOUNG的模式函数，绿色圈为Jason－1业务模式函数。

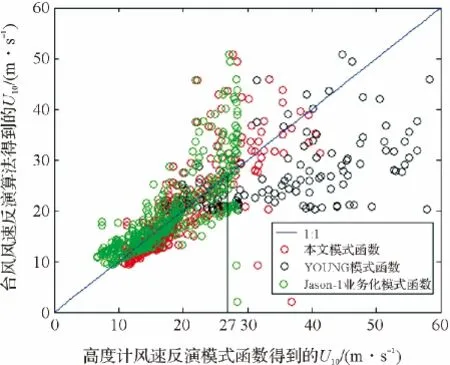
图3 本文提出的算法、Jason－1业务化算法和YOUNG算法结果与由台风风速反演算法计算的风速结果比较Fig.3 The results comparison of the wind speed by models developed in this study，the operational method of Jason－1and YOUNG with the wind speed by typhoon wind speed reversion algorithm，respectively

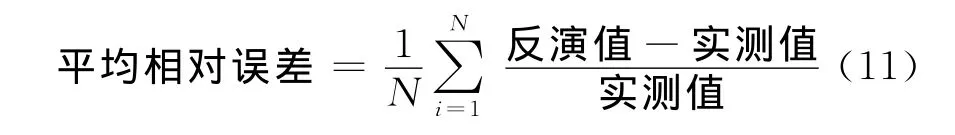
取风速小于27m／s，本文模式函数的RMS为3.38m／s，平均相对误差为18%；Jason－1业务化模式函数的RMS为3.60m／s，平均相对误差为19%。由此可以看出在风速较低时本文模式函数和Jason－1业务化模式函数的精度基本相同。当风速大于27m／s时，Jason－1业务化模式函数明显不再适用。为将本文模式函数和YOUNG模式函数作比较，取风速大于20m／s，本文模式函数的 RMS为6.27m／s，平均相对误差为16%；YOUNG模式函数的RMS为15.18m／s，平均相对误差为59%。由此可以看出本

由图3可以看出在风速小于27m／s时，本文模式函数和Jason－1业务化模式函数和台风风速反演算法比较结果都均匀地分布在1∶1附近，此时这两种模式函数都能较好地反映海表实际风速情况。我们采用均方根误差（Root Mean Square，RMS）和平均相对误差定量衡量这3种模式函数的优劣，平均相对误差的定义是：文模式函数能更准确地反演海表面的实际风速情况。因此本文给出的高度计风速反演模式函数具有广泛的适用性，可作为Jason－1高度计风速反演业务化算法的补充，以提高高度计风速反演精度。

3 结论

（1）通过与气象观测站实测资料对比，验证了HOLLAND台风风速反演算法在风速较小时会低估风速，风速较大时会高估风速；而YIN台风风速反演算法则可以准确反演台风风场。

（2）通过将YIN算法反演的台风风速和高度计后向散射系数对比提出了1个适用于高风速条件下的高度计风速反演模式函数。对比研究表明，由于YOUNG模式函数采用的HOLLAND台风风速反演算法自身缺点，使得其在低风速时反演值小于实测值，在高风速时反演值大于实测值；Jason－1业务化模式函数在低风速时能较好地反演实际风速情况，而在高风速时则不再适用，这是由于该模式函数在训练网络时使用的是散射计的风速资料，在强风情况下散射计严重低估海表面风速，导致该模式函数只适用于风速小于30m／s的情况。而本文提出的模式函数RMS和平均偏差都要优于以上两种模式函数，能更好地反映高风速时海面风场情况。因此本文的模式函数有更广泛的使用范围，可以作为Jason－1业务算法在高风速时的补充。

致谢感谢中国海洋大学刘应辰老师提供气象观测站资料，为本研究顺利进行提供支持；感谢审稿专家提出的宝贵意见！

（References）：

［1］LIU Yu－guang.Satellite oceanography［M］.Beijing：Higher Education Press，2009：206－230.

刘玉光.卫星海洋学［M］.北京：高等教育出版社，2009：206－230.

［2］DRAPER D W，LONG D G.Evaluating the effect of rain on sea winds scatterometer measurements［J］.J Geophys Res，2004，C12（109）：C02005，doi：10.1029／2002JC001741.

［3］WEISSMAN D E，BOURASSA M A，TONGUE J.Effects of rain rate and wind magnitude on SeaWinds scatterometer wind speed errors［J］.J Atmos Oceanic Technol，2002，5（19）：738－746.

［4］PICOT N，CASE K，DESAI S，et al.AVISO and PODAAC user handbook［M］.IGDR and GDR Jason Products.Ver.4.1.SMMMU－M5－OP－13184－CN （AVISO），2008，JPL D－21352 （PODAAC）.

［5］WITTER D L，CHELTON D B.A Geosat altimeter wind speed algorithm and a method for altimeter wind speed algorithm［J］.J Geophys Res，1991，C5（96）：8 853－8 860.

［6］YOUNG I R.An estimate of the Geosat altimeter wind speed algorithm at high wind speeds［J］.J Geophys Res，1993，C11（98）：20 275－20 285.

［7］HOLLAND G J.An analytic model of the wind and pressure profiles in hurricanes［J］.Mon Weather Rev，1980，8（108）：1 212－1 218.

［8］CARR L E，ELSBERRY R L.Models of tropical cyclone wind distribution and beta－effect propagation for application to tropical cyclone track forecasting［J］.Mon Weather Rev，1997，12（125）：3 190－3 209.

［9］YIN Xiao－bin，WANG Zhen－zhan，LIU Yu－guang，et al.Ocean response to Typhoon Ketsana traveling over the northwest Pacific and a numerical model approach［J］.Geophys Res Lett，2007，34（21）：L21606.

［10］POWELL M D.Evaluations of diagnostic marine boundary layer models applied to hurricanes［J］.Mon Weather Rev，1980，19（108）：758－766.

［11］LIU Yu－guang，SU Ming－yang，YAN Xiao－hai，et al.The mean－square slope of ocean surface waves and its effects on radar backscatter［J］.J Atmos Oceanic Tech，2000，17（8）：1 092－1 105.

［12］BROWN G S，STANLEY H R，ROY N A.The wind speed measurement capacity of space borne radar altimeter［J］.IEEE J Oceanic Engineer，1981，2（6）：59－63.

［13］CHELTON D B，MCCABE P J.A review of satellite altimeter measurement of sea surface wind speed：with a proposed new algorithm［J］.J Geophys Res，1985，C3（90）：4 707－4 720.

［14］CHELTON D B，WENTZ F J.Further development of an improved altimeter wind speed algorithm［J］.J Geophys Res，1986，C12（91）：14 250－14 260.

［15］ZHAO D，TOBA Y.A spectral approach for determining altimeter wind speed model functions［J］.J Ocean，2003，59（2）：235－244.

［16］GOURRION J，VANDEMARK D，BAILEY S，et al.A twoparameter wind speed algorithm for Ku－band altimeters［J］.J Atmos Oceanic Technol，2002，12（19）：2 030－2 048.

［17］JIN Tao－yong，LI Jian－cheng，WANG Zheng－tao，et al.Crosscalibration and validation of Jason－1and T／P altimeter data in their synchronous cycles［J］.Journal of Geodesy and Geodynamics，2007，27（6）：72－76.

金涛勇，李建成，王正涛，等.JASON－1与T／P测高卫星同步段数据比较分析［J］.大地测量与地球动力学，2007，27（6）：72－76.

［18］LEFEVRE J M，BARCKICKE J.A significant wave height dependent function for TOPEX／POSEIDON wind speed retrieval［J］.Journal of Geophysical Research，1994，C12（99）：25 035－25 049.