无约束线性映射对位形空间曲率的影响

王 勇，陈英华

（广东医学院 信息工程学院，广东 东莞523808）

0 引言

分析力学的研究总是伴随着人们对系统位形空间几何结构认识的不断发展和深化。从历史上看，“当力学系统加上约束时，由直角坐标过渡到广义坐标是特别方便的，而且也是十分必要的”［1］。事实上，从描述质点运动的牛顿力学过渡到描述完整约束系统的Lagrange力学的过程，也就是力学系统的位形空间从由坐标描述的、平直的欧几里得空间过渡到由广义坐标描述的、有曲率的Riemann空间的过程。而在非完整力学系统的研究中，则进一步引入了准坐标的概念。准坐标既可以通过非完整系统所受的非完整约束来定义［2－4］，也可以通过在完整力学系统的位形空间上复合一个同维数的非完整映射来定义［5－6］，因此，和广义坐标所描述的、有曲率的Riemann位形空间相比，由准坐标所描述的位形空间显然具有更加广泛的适用性。目前的研究已证明：由准坐标所描述的、受到一阶线性齐次非完整约束的系统的位形空间是既有曲率又有挠率的Riemann－Cartan空间。

笔者在之前的研究中提出了用一阶线性映射建立两个空间几何性质之间联系的方法，利用这一方法可以从力学系统一个已知的位形空间出发去构造新的、更加贴近系统物理实质的位形空间，从而在新的位形空间中使物理问题的研究得以简化。在随后的工作中，又将这一方法应用到非完整力学和刚体力学等领域的研究中，取得了一些有意义的成果［3－6］。在对这些问题的研究中，我们关注的是一阶线性映射的非完整性对系统位形空间挠率的影响，指出映射的非完整性正是位形空间挠率的来源，非完整映射把力学系统的一个普通的无挠率的位形空间映射为一个有挠率的Riemann－Cartan位形空间。在此过程中，一阶线性齐次非完整约束系统所受约束的非完整性被描述为空间挠率，从而实现了力学系统非完整性的几何化。

本文将在此基础上进一步研究一阶线性映射对系统位形空间曲率的影响。一般来说，如果一阶线性映射隐含约束，则约束会对系统位形空间的曲率产生影响，这一点无论从物理或几何直观上都很容易理解（例如，三维欧几里得空间中运动的一个质点受到一个完整约束时，位形空间一般就约化为三维欧几里得空间中的一个二维曲面）。本文将指出，映射的非完整性同样可能影响位形空间的曲率。为了清楚说明这一点，将讨论无约束的一阶线性映射对空间曲率的影响。显然，对隐含约束的一阶线性映射来说，本文的研究思路也一样适用，且能得到类似的研究结论。

本文采用爱因斯坦求和约定，指标取值范围都为1，2，…，n。

1 无约束线性映射对位形空间曲率的影响

考虑一个由n维Riemann位形空间［Y］（记该空间的广义坐标为yi，度规为gij，联络为）所描述的完整约束系统，设为空间［Y］的切空间上的一个无约束的线性映射，即：

则式（1）中的zρ构成了一个新的n维位形空间［Z］的切空间的基矢，计算可得位形空间［Z］的度规和联络分别为：

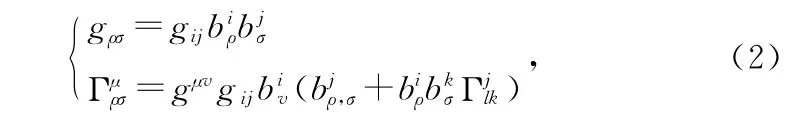
考虑到映射（1）不含约束，所以有：

其中aρi满足：

因此位形空间［Z］的联络可进一步化简为：

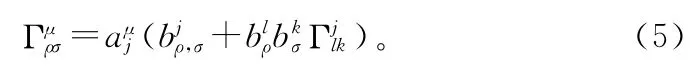
将式（5）带入标量曲率的公式［7］：

其中Rij为Ricci张量，定义为：

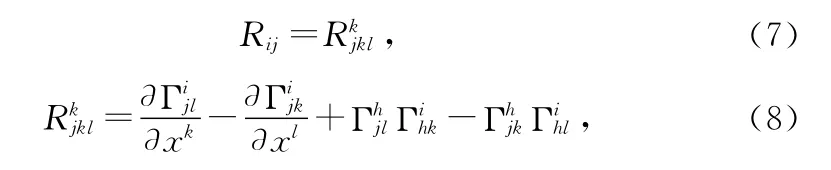
并考虑：

经过计算可以证明位形空间［Z］的标量曲率RZ为：

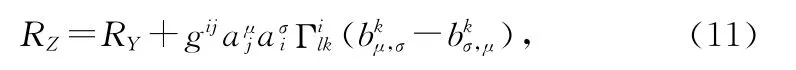
其中RY为位形空间［Y］的标量曲率。

如果映射（1）是无约束的完整映射，则容易证明位形空间［Z］仍然是一个Riemann空间，且此时因为有

由式（11）可以看出空间的标量曲率将保持不变；从物理的角度看，此时无约束的完整映射就相当于同一个位形空间中广义坐标之间的变换。而如果映射（1）是无约束的非完整映射，则式（12）不再成立，位形空间［Z］将是一个有挠率的Riemann－Cartan空间，且由式（11）可以看出，无约束的非完整映射不仅使系统的位形空间出现挠率，而且一般来说曲率也同样发生了变化（一个例外是：如果空间［Y］是一个联络为零的平直空间，则由式（11）容易看出，即使映射（1）是无约束的非完整映射，空间［Z］的曲率仍然为零，保持不变，此时空间［Z］是一个有挠率、无曲率的特殊的 Riemann－Cartan空间——Weitzenbock空间）。

2 算例

考虑一个约束在单位球面上的、具有单位质量的质点，其位形空间［Y］是一个三维欧几里得空间中的单位球面，取球面坐标系中的仰角θ和方位角φ为广义坐标y1和y2，计算可得其度规、联络、标量曲率和挠率分别为：

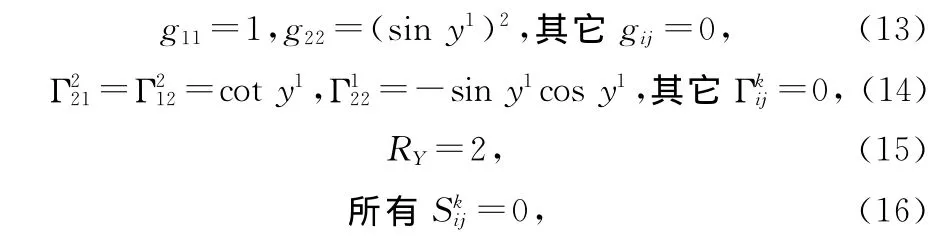
显然，此时位形空间［Y］是一个常曲率、无挠率的Riemann空间。

如果在单位球面［Y］的切空间上引入一个无约束的线性映射：

容易验证映射（17）是一个非完整映射。将式（13），（14），（17）带入式（2），可得位形空间［Z］的度规和联络分别为：

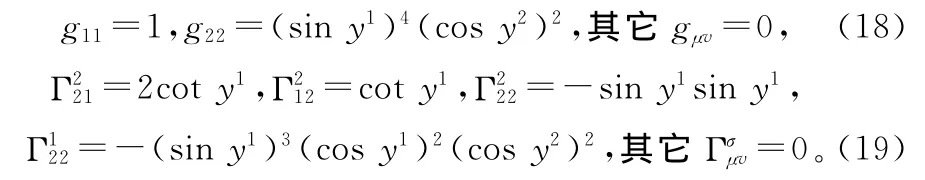
进一步计算可得位形空间［Z］的标量曲率和挠率分别为：

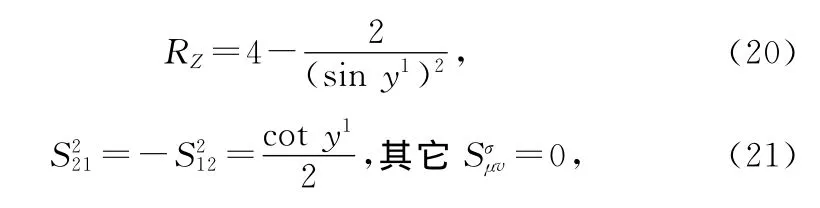
这说明位形空间［Z］是一个变曲率且有挠率的Riemann－Cartan空间。显然，无约束非完整映射（17）不仅使质点的位形空间具有了挠率，而且也改变了位形空间的曲率。

3 结论

从物理的角度看，完整的无约束线性映射相当于约束系统位形空间不同广义坐标之间的变换关系，这种变换并不改变位形空间的曲率和挠率，因此本质上只是描述同一个位形空间的不同广义坐标之间的变换。相对而言，非完整的无约束线性映射则要复杂得多，这种映射不仅会给位形空间带来挠率，而且也改变了空间的曲率。由于没有约束，显然此时空间曲率的变化是由于映射的非完整性所造成的。这说明映射的非完整性不仅能表现在空间挠率的变化上，而且也能表现在空间曲率的变化上，这从一个侧面体现出非完整问题的复杂性。同时也说明，和挠率一样，位形空间曲率的变化也能反过来反映出两个位形空间之间映射的非完整性。

［1］ 梅凤翔．分析力学：上卷［M］．北京：北京理工大学出版社，2013：12．

［2］ Kleinert H，Shabanov S V．Space with torsion from embedding，and the special role of autoparallel trajectories［J］Phys Lett B，1998，428：315－321．

［3］ Guo Y X，Wang Y，Chee G Y，et al．Nonholonomic versus vakonomic dynamics on a Riemann－Cartan man－ifold［J］J Math Phys，2005，46（5）：062902．

［4］ 王勇，郭永新．Riemann－Cartan空间中的d’A1embert－Lagrange 原 理 ［J］．物 理 学 报，2005，54（12）：5517－5520．

［5］ 王勇，郭永新，吕群松，等．非完整映射理论与刚体定点转动 的 几 何 描 述 ［J］．物 理 学 报，2009，58（8）：5142－5149．

［6］ Guo Yongxin，Liu Chang，Wang Yong，et al．Nonholonomic mapping theory of autoparallel motions in riemann－cartan space［J］．Science China（Physics，Mechanics ＆ Astronomy），2010（9）：1707－1715．

［7］ 余扬振，冯承天．物理学中的几何方法［M］．北京：高等教育出版社；海德堡：施普林格出版社，1998：487．