振动筛上振动横梁的疲劳应力分析
2015-05-14孙皆宜
孙皆宜
(唐山学院 基础教学部,河北 唐山063000)
0 引言
在选煤工艺中振动筛主要用于煤泥粗颗粒的脱水与脱泥,它由振动电机带动弧形筛箱体从而产生振动。在洗煤厂现场的使用过程中,有些振动筛在工作一段时间后振动横梁就会出现裂纹,且一般出现在振动电机底座附近,呈横向,破坏形式主要表现为疲劳失效。这是由于金属的表面和内部结构并不均匀,从而造成应力传递的不均衡,有的地方会形成应力集中区[1]。此外,金属内部还存在许多微小裂纹的缺陷,在交变应力的持续作用下,裂纹会越来越大,材料中能够传递应力的部分越来越少,直至剩余部分不能继续传递负载,金属构件就会被完全破坏[2]。因此,预测结构或零部件的随机疲劳寿命非常必要[3]。
疲劳寿命是机械设备的主要设计目标之一。然而在设计阶段要检验一个产品的优劣往往需要对样品进行试验,这样不仅加大了成本投入而且过程繁琐。本文将利用疲劳应力理论和有限元分析软件ANSYS-Workbench,以疲劳寿命为依据,对振动横梁在正常工作环境下的应力分布和疲劳寿命进行分析,为提高振动横梁设计和制造的可靠性提供参考。
1 疲劳应力理论分析
造成疲劳破坏的重复变化应力叫作疲劳应力,用S来表示。结构在疲劳应力的作用下产生疲劳裂纹,直至疲劳失效所承受的循环应力次数N叫作结构的疲劳寿命。表示应力幅与疲劳寿命之间关系的曲线称为疲劳曲线或S-N曲线[4]。其表达式为:

其中,m和C与材料特性、载荷的形式、零件的尺寸等因素[5]有关。式(1)两边取对数可以得到:
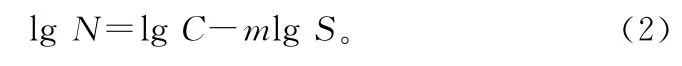
因此,对于某一具体结构,疲劳寿命与应力之间存在对数线性关系。
为了估算振动横梁的疲劳寿命,除了S-N曲线外,还需要借助疲劳累积理论[6]。累积理论可以概括为三种类型,即线性累积损伤理论、修正线性理论和其它理论。其中线性累计损伤理论形式简单,且有一定的精度,在工程上得到了广泛应用。线性累积损伤理论认为在各种循环载荷作用下的疲劳损伤可线性累加起来,各应力之间相互独立和互不相干,当累加损伤达到一定数值时,试件或构件就发生疲劳破坏,即:
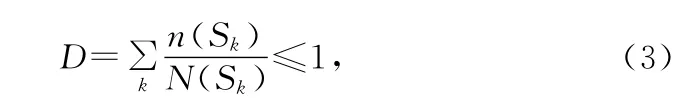
式中D为构件的总损伤。Sk为对称循环应力,n(Sk)为在Sk作用下循环次数,N(Sk)为疲劳寿命,将式(1)代入式(3)得:

当式(4)中的D等于1时,部件发生疲劳破坏。在结构的设计中,通常采用有限元分析来预估算疲劳寿命。
2 振动梁的疲劳应力有限元仿真
ANSYS-Workbench有限元分析软件具有强大的疲劳分析功能[7-8],通过定义疲劳载荷、材料疲劳特性,选择合适的疲劳准则,综合各种影响因素,根据等应变等损伤假设,经过雨流计数,对工作循环的载荷时间历程或局部应力-应变进行统计处理,将每个循环的疲劳损伤都计算出来,进而通过累积损伤计算预测构件的疲劳寿命。
将利用建模软件Creo建立的振动横梁的三维模型导入到Workbench中,设置材料属性为结构钢,其弹性模量E=200 GPa,泊松比p=0.33,屈服极限σb=235 MPa,并利用Workbench软件对振动梁自动划分网格。在振动横梁两端添加约束。并在振动梁中间4个电机安装孔处设置对称循环载荷,如图1所示。
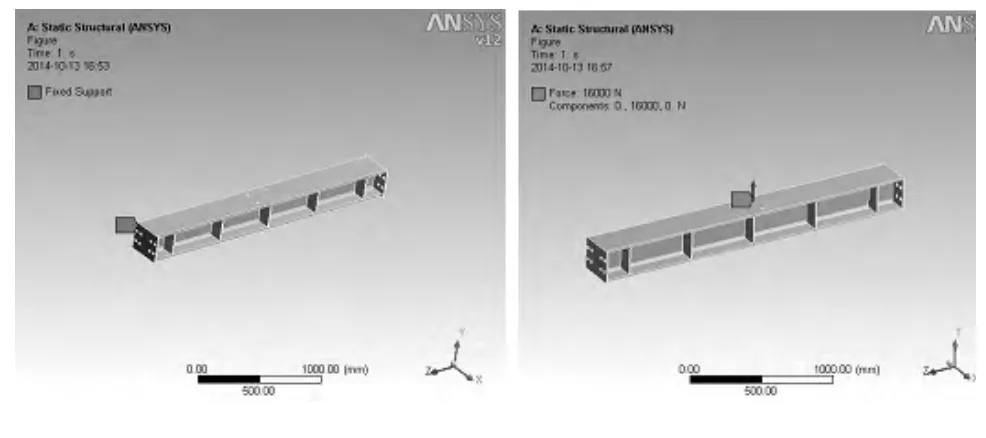
图1 振动梁约束与受力示意图
在振动弧形筛工作过程中,振动横梁所受的交变应力可以近似认为是大小为16 000 N,频率为15.17 Hz的对称循环载荷,建立的交互应力循环如图2所示。
取振动梁疲劳强度因子为0.8,设定振动梁疲劳寿命为109循环次数,求解得到振动梁应力、安全系数分布分别如图3,图4所示,振动横梁各位置的最小安全系数为3.32,振动横梁所受最大疲劳应力为20.79 MPa,局部高应力区域在振动电机安装底座附近,与实际破坏位置相吻合。
最后分析振动梁的疲劳敏感性,即确定振动梁在满足疲劳寿命的情况下所能承受的最大循环载荷。对定义的一个最小基本载荷变化幅为100%(一个16 000 N的对称循环应力)和一个最大基本载荷变化幅为400%(一个64 000 N的对称循环应力)的交变应力进行分析,得到振动梁的疲劳寿命变化曲线如图5所示。

图2 交互应力循环图

图3 振动梁应力图

图4 振动梁安全系数分布图
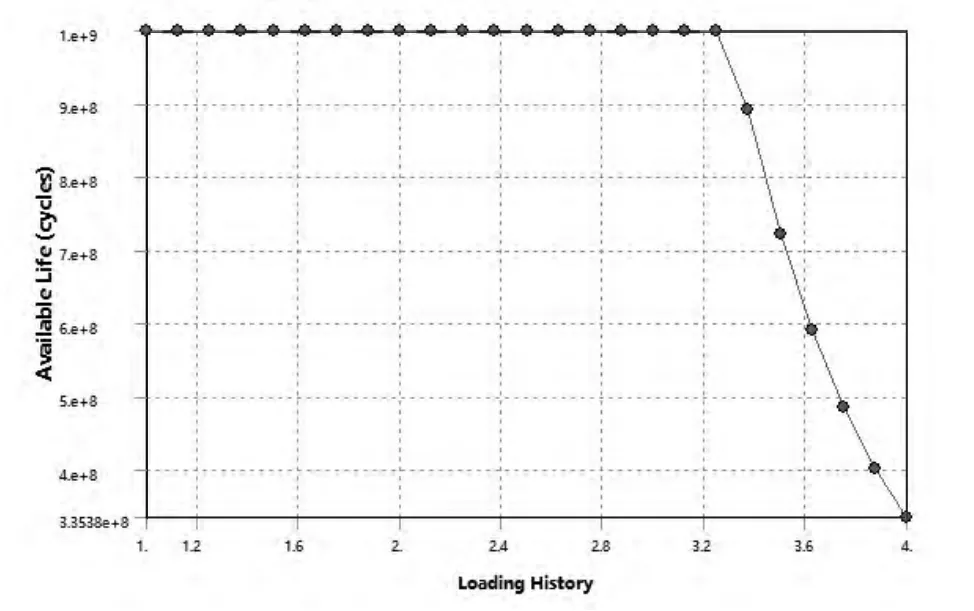
图5 振动梁随交变应力变化的疲劳寿命曲线
由图5可以看出,当交变应力上升到大约为设计应力的3.2倍(51 000 N)时振动梁的疲劳寿命才出现明显缩短,这也符合了前面对振动梁安全系数的分析。对于本振动弧形筛而言,在实际工作中这种交变应力几乎是不可能达到的,所以,对于该振动梁的设计,符合疲劳应力的要求。
3 结论
(1)疲劳应力校核表明,振动筛横梁的最大应力远远小于材料的屈服极限,验证了振动横梁的破坏不是由静强度不足引起的,而是因为交变应力的持续作用产生的疲劳所致。
(2)经分析,振动梁的振动次数可达109次。以振动电机每分钟910 r/min计算,振动梁可保证使用18 315 h,按振动弧形筛每天工作16 h计算,振动梁的疲劳寿命为1 144 d,至少使用3年不会出现疲劳破坏。
[1] 吴镇,石端伟.大型升船机船箱门静力与疲劳有限元分析[J].起重运输机械,2007(12):44-45.
[2] Anon.Fatigue resistance[J].Advaneed Materials and Proeesses,1990,137:89-94.
[3] 徐灏.疲劳强度[M].北京:高等教育出版社,1988:121.
[4] Joosten M W.New study shows how to prediet aeeumulated drill pipe fatigue[J].World Oil,1985,196:65-70.
[5] 徐才发,李伟.起重机主梁舱门处开裂的故障分析[J].起重运输机械,2000(9):32-35.
[6] 曾春华,邹十践.疲劳分析方法与应用[M].北京:国防工业出版社,1991:11.
[7] 徐玉兴.转子强度及疲劳寿命分析[J].理论与研究,2008(2):1-8.
[8] 姜年朝.ANSYS和 ANSYS/FE-SAFE软件的工程应用实例[M].南京:河海大学出版社,2006:72-73.
