集合标准型与原型中文译名探析和求法比较

廖轲

摘要：音级集合理论作为最重要的后调性（post-tonal）理论之一，其在音乐理论领域中具有举足轻重的地位，从音乐理论家弥尔顿·巴比特（Milton Babbitt）最早提出集合理论以来，音级集合理论经历了几十年的发展，但直到二十世纪八十年代才被我国音乐理论学者引入国内，本文就以音级集合理论中的标准型和原型这两个基本概念的求法比较作为切入点来进行介绍和探讨，并结合国内涉及集合理论的一些译著与学术论文，对这两个概念的中文译名进行比较概述。

关键词：音级集合 标准型 原型 中文译名 求法比较

一、音级集合理论的国内外发展概述

音级集合理论所经历的发展时间与其他后调性理论比起来并不长，最早提出集合理论的是美国音乐理论家弥尔顿·巴比特（Milton Babbitt），他可以被看作是集合理论的开创性人物，其一生为音乐理论事业做出了巨大贡献，并且为后世留下的大量理论文献与资料。美国的另外一名著名的音乐理论家艾伦·福特（Allen Forte）便是基于巴比特对于集合理论早先的研究，形成了一本关于音级集合理论的专著——《无调性音乐的结构》（The Structure of Atonal Music）。现如今，在国外设计集合理论研究的著作和文献越来越丰富，理论研究越来越向前延伸。

而国内的关于集合理论的专著与译著较少，具有代表性的如艾伦·福特著、罗忠镕翻译的《无调性音乐的结构》；罗伊格·弗朗科利（Roig Francoli）著、杜晓十与檀革胜合译的《理解后调性音乐》；以及约瑟夫·N·斯特劳斯（Joseph N Straus）著、高畅与常沁轲合译的《后调性理论导读》（第三版）①等几本译著，本文对集合标准型与原型的求法均依据自这几本译著。由于每个译者对原著内容理解的不同，使得在对一些理论概念翻译的表述上存在些许差异。因此有很多在国外已经统一了的定义和概念，在翻译成中文时会存在偏差，甚至混淆的情况。笔者就以集合理论中标准型和原型这两个基本概念进行概述，比较其中文译名的差异和总结标准型与原型的求法。

二、标准型和原型中文译名探析

（一）标准型概述与译名比较

标准型②原文名称为“normal form”③在艾伦·福特所著《无调性音乐的结构》中，原文名称为“normal order”，中文被译作“标准序”④。但在实际在概念意义上，它们都是表达的一个概念。定义的表述可以总结为，集合理论中的标准型是指对于一个音级集合，我们以有序（上行升序）排列的方式进行排列，使其成为最简单、最紧凑的一种形态。笔者认为，标准型是对集合最标准形态的一个界定，标准序则是从集合标准顺序的解释，但由于需要与原型这一概念有所区别，所以笔者更偏向于标准型的称谓。标准型的记法为把集合元素或音级数置于方括号内并用逗号隔开，如[C，D，E，G]或[0，2，4，7]。

（二）原型概述与译名比较

原型的原文名称为“prime form”⑤，在罗伊格·弗朗科利著，杜晓十与檀革胜合译的《理解后调性音乐》中“prime form”被译为基本型，笔者倾向于原型的表述。它是指通过对一个集合族中所有集合进行观察后，从中选出的一个“最标准”的标准型来作为整个集合族的名称。在福特的著作中，他把原型解释为把一个标准型进行首位集合元素为0的移位。需要注意的是，原型的表示方法与标准型不同，原型的表示方法在括号内的不带逗号隔开的一组数字，如（0145）。

三、标准型和原型求法比较

（一）标准型的求法

求标准型的方法笔者归纳为两大类：排列求差法与音级钟面图法。

1.排列求差法

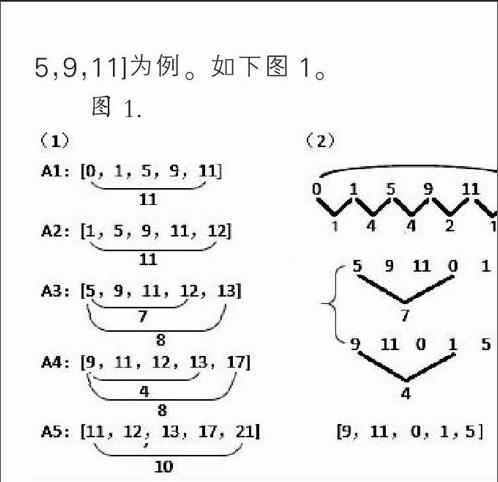
排列求差法具体指的是对一个音级集合的集合元素进行从小到大（或从下到上）的升序式循环排列，并对每个排列进首尾两数之差的计算，差数最小则首尾两音的音程距离最短，即为最紧凑排列，即为标准型。如果有两种以上的排列存在首尾两数差相同的情况，则进行第二步，求首位数与倒数第二数之差，若还是存在相同差的情况则继续求首位数与倒数第三位数之差，依次下去，直到求出首位数与其他位数差数最小的最紧凑排列为止。在运用排列求差法来求标准型时，具体的求差步骤也会些许不同，我们以集合[0，1，5，9，11]为例。如下图1。

图1.

从图1—（1）可以看出排列求差法的具体步骤，把集合[0，1，5，9，11]进行循环排列后得到5个集合，每组首尾之差相比较，我们会发现A3集合与A4集合首尾之差相同，把这两个集合进行首位数与倒数第二数之差比较，能看到A3的首位数与倒数第二数之差为7，A4的首位数与倒数第二数之差为4。因此我们能够得出结论，即A4的集合排列是最紧凑最密集的排列，A4即为集合[0，1，5，9，11]的标准型。按照mod12（模12）的概念，A4集合为[9，11，0，1，5]。这种排列求差的具体方法与步骤可以参见艾伦·福特著，罗忠镕译的《无调性音乐的结构》。

在具体实践中，我们会觉得把一个集合进行循环排列再求首尾数之差会很繁琐，耗费很多时间，因此我们可以采用一种更为简便的方法，如图1-（2）所示。图中我们把集合中的各元素按升序依次排列出来，并把首位音在最后提高八度重复，然后比较每个元素之间的音程距离，寻找出最大的音程，然后以最大音程的上方音为首位音再进行顺序排列。从图中我们找到的最大音程距离是4，并且有两个，因此我们把这两种可能构成标准型的集合进行排列，进行第二步，寻找首位数与倒数第二位数之差，结果我们会发现差数最小的集合是[9，11，0，1，5]。因此，该集合就是标准型。这种操作方法和步骤可以参见罗伊格·弗朗科利著，杜晓十与檀革胜合译的《理解音级集合音乐》。

我们可以把排列求差法的步骤在五线谱上表现出来，这样就会显得比较直观。如下图2。

图2.

2.音级钟面图法

我们知道，一个八度内共有12个半音，试想这12个半音和钟表上的12个指针不是一一对应的么。因此以钟面为蓝本进行12音的排序来确定12个半音之间的音程距离关系就是音集钟面图法。用音集钟面图来确定集合内各元素的音程距离并求出集合标准型，相比较于排列求差法来说是一个简单快捷的方式，并且从视觉上也很直观，还是以集合[0，1，5，9，11]为例。参看下图3。

图3.

在钟面图上，我们把集合元素标记出来，它们之间的距离关系一目了然，按照最密集最、紧凑的有序排列方式，我们自然而然的能够排列出集合标准型了，即[9，11，0，1，5]。钟面图分析方式可参见约瑟夫·施特劳斯著，高畅、常沁轲译《后调性理论导读》。

对于求集合标准型，在方式方法上有很多办法，具体的操作步骤也有很多，但标准只有一个——即最密集、最紧凑。用调性和声的语言来讲，就是把集合看成一个和弦，最密集紧凑的和弦就是原位和弦，因此求标准型就如同求一个原位和弦。

（二）原型的求法

求集合原型的步骤相比较于求标准型则比较统一，首先要先找出集合的标准型，这就需要先进行求标准型的步骤，然后再对标准型进行移位，移位的结果必须是首位集合元素为0。以集合[3，5，7，8]为例，这已经是一个标准型集合了，然后对其进行首位集合元素为0的移位，即T9移位，然后得到新集合[0，2，4，5]，然后我们会发现，新得到的集合元素之间的距离并不是从左到右最紧凑的形式，因此它不是真正的原型，因此我们需要对该集合进行倒影操作，并重新置于标准型再移位。最后我们得到的原型就是（0135）。

利用音级钟面图我们同样能很快找出集合[3，5，7，8]的原型。如下图4所示。

图4.

四、结语

音级集合理论作为现代音乐理论领域中最重要的理论之一，其不仅作为一种作曲手法，更重要的在于其作为一种专门的分析方法，对分析无调性的音乐作品，特别是分析那些以音高级组合为基础的、有意避免音高中心性的音乐作品的材料结构⑥，具有很好的优势。以上就是笔者总结的集合理论中求标准型与原型的方法，以及对其译名概念的解析。

注释：

①注：由于引进版权的问题，高畅教授与常沁轲合译的版本未能在国内出版，现仅作为四川音乐学院内部资料使用。

②标准型（以及下文的原型）的中文译名名称均来自于约瑟夫·N·斯特劳斯（Joseph N Straus）著，高畅与常沁轲合译的《后调性理论导读》（第三版）。

③“normal form”这一概念是由约翰·拉恩（John Rahn）在其著作《基础无调性理论》（Basic Atonal Theory）中提出，在约瑟夫·N·斯特劳斯（Joseph N Straus）著《后调性理论导读》中介绍原型时采用了拉恩的描述。

④参见[美]艾伦·福特《无调性音乐的结构》，罗忠镕译，上海：上海音乐出版社，2013年第4页。在罗伊格·弗朗科利（Roig Francoli）著，杜晓十与檀革胜合译的《理解后调性音乐》一书中也是采取的这种名称。

⑤“prime form”这一概念同③。

⑥[美]罗伊格·弗朗科利：《理解后调性音乐》，杜晓十，檀革胜译，北京：人民音乐出版社，2012年第71页。

参考文献：

[1][美]艾伦·福特.无调性音乐的结构[M].罗忠镕译.上海：上海音乐出版社，2013.

[2][美]约瑟夫·施特劳斯.后调性理论导读[M].高畅，常沁轲译.成都：四川音乐学院内部资料，2013.

[3][美]罗伊格·弗朗科利.理解后调性音乐[M].杜晓十，檀革胜译.北京：人民音乐出版社，2012.

[4]高畅.后调性理论中一些概念术语解析及中译名琐谈——翻译斯特劳斯《后调性理论导读》一书后的思考[J].音乐时空，2013，（12）.

[5]高畅.对拉恩和福特集合标准型及原型标准的比较评析[J].中央音乐学院学报，2015，（01）.