初等函数值域(最值)的导数求法
2015-05-10林顺来杨朝熙
林顺来 杨朝熙
(漳州市第三中学,福建 漳州 363000)
初等函数值域(最值)的导数求法
林顺来 杨朝熙
(漳州市第三中学,福建 漳州 363000)
函数值域、最值问题历来是教学中的重、难点。由于没有通性通法,学生往往难于找到有效的解决方法。文章从可导函数的单调性出发,运用函数极值、极限等知识获得值域、最值的导数求法,从而得到一种通法。
值域;最值;求导;极值;极限
我们知道对于给定函数解析式y=f(x)的值域由函数的定义域及其对应法则唯一确定,确定的方法是针对函数的类型选取相应的方法:(1)若为特殊的基本初等函数(正比例函数反比例函数、一次函数、二次函数、指数函数与对数函数、三角函数与反三角函数、幂函数等),这类函数的值域问题利用它们定义域上的单调性求解。(2)若为复合函数,可以利用其定义域上的单调性(判定方法是:通过复合前基本初等函数的单调性并循“同增异减”的法则)来获得值域。(3)其他的基本初等函数的值域,通常的处理方法是:对解析式的特征选取特定的方法加以解决(常见的方法有:二次函数型的配方法、反函数法、判别式法、数形结合法、不等式法、函数的有界性法等[1])。由于没了共性通法,教学中学生往往感到困难。能否找到这类问题的通性通法?笔者在教学中发现,处理问题的关键在于搞清此类函数在其定义域内的单调性,若知道它的单调性情况便可求其值域。随着教材中《导数》的学习,使得“可导函数”的单调性判断成为可能。同时在《普通高中课程标准实验教科书·数学》(文科选修1-1、理科选修2-2“导数及其应用”)专门辟出一节讨论可导函数的最大值与最小值:
一、闭区间上函数的最值
设函数f(x)在[a,b]上连续,在(a,b)内可导,求f(x)在[a,b]上的最大值与最小值的步骤如下:
(1)f(x)在(a,b)内的极值;
(2)将f(x)的各极值与f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值。
二、单峰函数的最值
可导函数在其定义域(区间)内只有一个点使f′(x)=0,如果函数在这点有极大(小)值,那么不与端点值比较;也可以知道这就是最大(小)值。这里所说的定义域(区间)也适用于开区间或无穷区间。
上述两点的指导意义:提供了可导函数y=f(x),x∈D最值的导数求法,利用这种方法同样可以求函数的值域:
若函数y=f(x)是定义在闭区间[a,b]上连续,开区间(a,b)上可导。那么函数y=f(x)的值域即为最大值与最小值。(1)f′(x)=0令解出方程在定义区间上的根;(2)比较f(x)在方程f′(x)=0的根处的函数值与端点处的函数值,就能得出最大最小值。
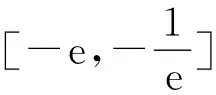
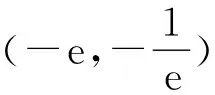
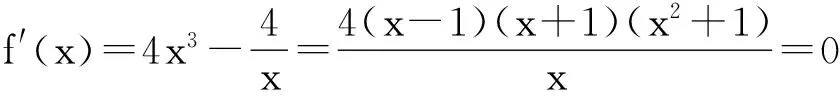
得可疑点x=-1,x=1(不合题意舍去)
通过比较,可见函数f(x)=x4-1nx4有最大值e4-4,最小值1.
求可导函数在闭区间上的最值的过程中,当得出可疑点,无须再检验它是否为极值点,而直接将可疑点与端点处的函数值进行比较,这是与求可导函数的极值不同的地方[2]。
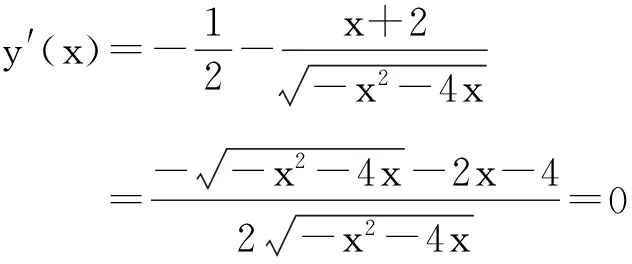
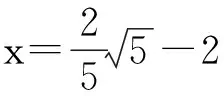
计算函数在可疑点与端点处的值为:
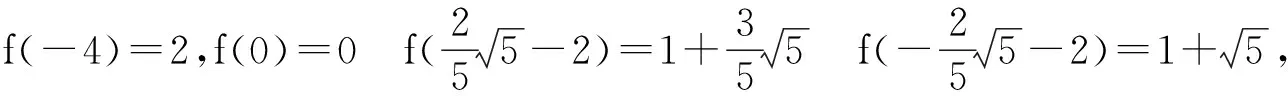
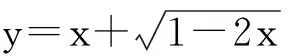
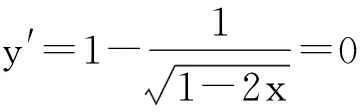
又∵当x∈(-∞,0)时,y′>0
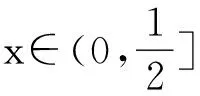
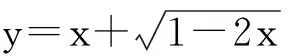
对于无理函数的值域问题,传统解题思路要么通过平方去掉根号,再根据二次函数的一些性质求值域;或者通过换元,令其中一项等于t,将原函数转化为关于t的函数求解。这两种方法在实际操作中没那么容易,学生遇到这类问题心理上会产生畏惧感,若用可导函数在闭区间上的最值求法,就会显得自然。例3解法利用单峰函数的函数性质获得值域,解决了导数在求闭区间上可导函数值域的一般性方法。
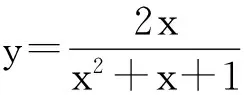
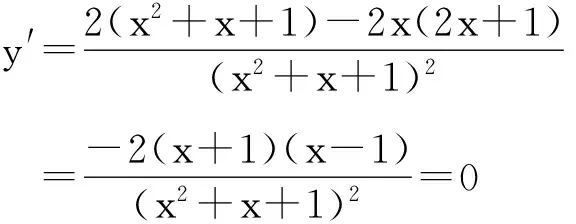
得可疑点x=-1,x=1;当x∈(-∞,-1)时,y′<0;
当x∈(-1,)时,y′>0;
当x∈(1,+∞)时,y′<0。
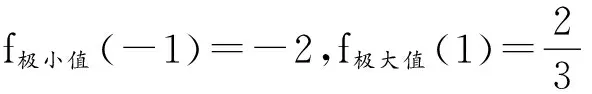
当x→+∞时,y充分接近0.
注:本题的导数法以及函数极限在求值域中的运用。至此,可导函数在其定义域上的值域均可用上面的方法获得。
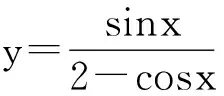
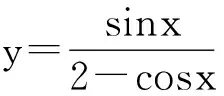
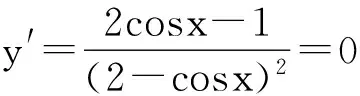
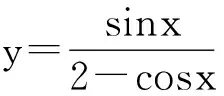
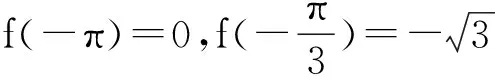
通过上面的分析,对一般的初等函数,求函数的最大(小)值基本的方法是通过函数的单调性来判定,它的最值必在下列各点中取得:导数为零的点、导数不存在的点、端点。关键在于对不可导的连续点,开区间或无穷区间内最大(小)值的分析,借助导数知识使得初等函数的最值问题获得全新的思路和方向。
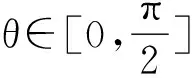
解:∵f(x)是R上的奇函数,且在[0,+∞)上是增函数,∴f(x)是R上的增函数.于是不等式可转化为f(cos2θ-3)>f(2mcosθ-4m),即cos2θ-3>2mcosθ-4m,即cos2θ-mcosθ+2m-2>0.
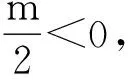
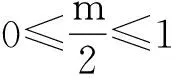
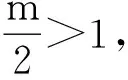
数学高考中经常涉及方程或不等式中参数的取值范围的考查。在解与不等式或方程有关的问题时,此类问题常常运用分离参数法转化为函数的值域或最值获得解决。我们往往由于忽略变换的等价性而产生错误的解答,如果能恰当地利用导数解法,利用函数单调性,则会避免这种错误.下面的两道高考题笔者给出异于参考答案的导数解法,从中体会导数在解决最值问题的极大优势:
(Ⅰ)求f(x)的单调区间和值域;
(Ⅱ)设α≥1,函数g(x)=x2-3α2x-2α,x∈[0,1],若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求x∈[0,1]的取值范围.
通过比较可知:当x∈[0,1]时,f(x)的值域为[-4,-3].
(Ⅱ)对函数g(x)求导,得g′(x)=3(x2-α2)
因此α≥1,当x∈[0,1]时,g′(x)<3(1-α2)≤0
因此当x∈[0,1]时,g(x)为减函数,从而当x∈[0,1]时有g(x)∈[g(1),g(0)]
又g(1)=1-2α-3α2,g(0)=-2α,即当x∈[0,1]时有g(x)∈[1-2α-3α2,-2α]
任给x1∈[0,1],f(x1)∈[-4,-3],存在x0∈[0,1]使得g(x0)=f(x1),则[1-2α-3α2,-2α]⊃[-4,-3]
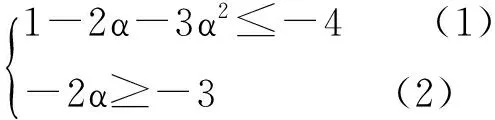
例8.(数学高考上海春招)设函数f(x)=|x2-4x-5|
(1)在区间[-2,6]上画出函数f(x)的图像;
(2)设集合A={x|f(x)≥5},B=(-∞,2]∪[0,4]∪[6,+∞],试判断集合A和集合B之间的关系,并给证明.
(3)当k>2时,求证:在区间[-1,5]上,y=kx+3k的图像位于函数f(x)图像的上方.
解:(1)、(2)略.
对于(3)的,标准答案给出两种方法。下面笔者利用导数的方法给出另一较为简便的解法:
分析:构造函数f(x)=kx+3k-|x2-4x-5|,x∈[-1,5],将题目转化为探求函数f(x)=kx+3k-|x2-4x-5,x∈[-1,5],求使f(x)>0恒成立的常数k的取值范围.
解:∵x∈[-1,5],|x2-4x-5|=-x2+4x+5;x+3>0
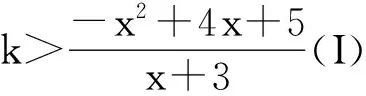
只需求t(x)当 x∈[-1,5]上的最大值t(x)max 解得可疑点x=1或x=-7(舍去) 计算t(-1)=0,t(1)=2,t(5)=0通过比较可知t(x)在区间[-1,5]上的最大值为t(1)=2. ∵不等式(I)恒成立的参数k的取值范围是k>2.因此,当k>2时,在区间[-1,5]上,y=kx+3k的图像位于函数f(x)图像的上方. 回顾整个解题过程,解决问题的本质在于将不熟悉的问题通过化归与转化的思想变形为熟悉的类型。笔者通过这个问题的探讨,希望能够更好的启发学生灵活运用所学知识,多思考,善于发现数学的本质,提炼和掌握解决问题的通性通法。 [1]王后雄.课标导航·高中基础知识手册(数学)[M].广西:接力出版社,2008. [2]任鸿志.高中优秀教案·数学(A)·必修Ⅰ[M].山东:南方出版社,2007. 2014-11-05 林顺来(1964- ),男,福建平潭人,漳州市第三中学特级教师。 G622.0 A< class="emphasis_bold">文章编号:1673-9884(2015)02-0055-04 1673-9884(2015)02-0055-04