做好课堂教学五个铺垫 提高基础薄弱生数学成绩

黄清钿

(大田县第五中学，福建 大田 361000)

做好课堂教学五个铺垫 提高基础薄弱生数学成绩

黄清钿

(大田县第五中学，福建 大田 361000)

铺垫教学是提高基础薄弱生数学成绩的有效教法。高中数学教学在新课引入、概念教学、公式定理教学、解题教学、教学难点突破等方面进行铺垫，有利于加深基础薄弱生对数学知识的理解和应用。

高中数学；铺垫教学；方法

我校是一所二级达标完中，新生数学基础薄弱的比例很大。面对这样的生源，课堂教学需要降低难度，放慢进度，在教学过程多些铺垫教学，少些跳跃，这有利学生对所学知识的理解。

一、做好新课引入的铺垫，激发学生学习兴趣

不管上什么课，如果是开门见山地向学生说明今我们要学习的内容是什么，学生对听课就打不起精神，听课是被动的，所以有经验的教师都会在讲新课前进行情境引入以吊起学生的听课“胃口”，因此有必要对所要学习的内容进行适当的铺垫。课堂引入的铺垫是指通过一个故事实例或复习一个知识点等方式对将要学习的内容作铺垫，产生“未成曲调先有情”的效果，拉近新旧知识的距离，降低知识的难度，激发学生学习的欲望。例如，在上等差数列的前n项和公式时，先介绍高斯小时候速算1加到100的故事，并提问：“高斯是怎样快速得到1+2+3+…+100的和的？高斯这种方法是否能推广到一般的等差数列？”通过师生互动解决这两个问题。这种铺垫既有故事性，又有思考性，能调动学生听课的积极性，同时用从特殊到一般的方法来学习等差数列的前n项和公式可达到水到渠成的效果。

二、做好概念教学的铺垫，新旧知识平稳过渡

高中数学的许多概念，课本里都是直接定义的，而这些定义一般都比较抽象，学生不易理解，学生自学或教师直接讲解都会使许多学生一知半解，学习效果并不好。在引进定义前，先举出适当的例子作铺垫，通过从特殊到一般，从具体到抽象，从简单到复杂的举例子方法降低学习难度有利于学生更好地理解概念。例如，偶函数这一概念的描述比较抽象，学生自学或教师直接讲解，学生对这一概念的理解处于一知半解状态，在解决实际问题中不能很好地应用。对这一概念的教学可先对此概念的形成进行一些铺垫：让学生观察熟悉的函数f(x)=x2,g(x)=|x|的图象，这两个函数的图象关于y轴对称。教师提出问题：你能从数的角度说明它们为什么关于y轴对称吗？学生通过探究，发现自变量x的值对称着取，其函数值相等，即x取互为相反数的两个值，他们的函数值相等。教师再问：是对所有的x都成立吗？于是，学生计算f(-x)与f(x)，发现相等。这时教师给出这类函数的名字为偶函数，然后再来学习课本中的定义就容易理解多了。

三、做好公式定理的铺垫，加深公式定理理解

在教学过程如果对公式、定理直解进行解读讲授，那么学生即使能理解也很难能进行灵活运用。知识只有通过发现或弄清其形成过程的获得，才能更好地消化吸收，准确应用。对于基础薄弱的学生更需要讲清公式、定理的来龙去脉。因此，教学过程做好公式、定理的铺垫有利于学生对公式、定理的消化理解。例如，在讲授直线与平面垂直的判定定理时，可进行如下教学铺垫：如下图，让学生在自己准备好的纸片上任意画一△ABC(∠B、∠C不为钝角)，然后将此三角形剪下，过△ABC的顶点A翻折纸片，得到折痕AD(D在边BC上)，将翻折后的纸片竖起放置在桌面上(BD，DC与桌面接触)，并提问学生——①折痕AD与桌面垂直吗？②如何翻折才能使折痕AD与桌面所在平面α垂直？

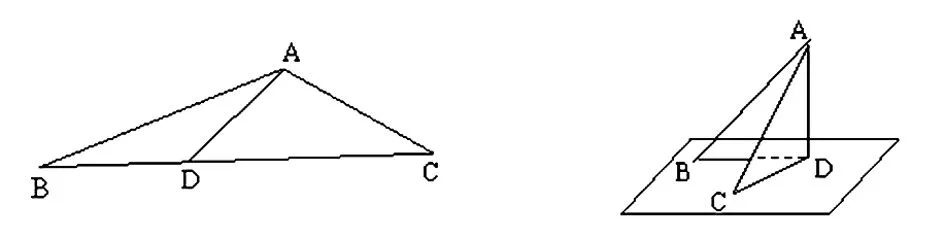
通过实验，学生容易发现，当且仅当折痕AD是BC边上的高时，AD所在直线与桌面所在平面α垂直。并引导学生观察，这个三角形翻折之后AD与CD、BD是否分别垂直。此时，进一步提问：(1)有人说，折痕AD所在直线与桌面所在平面α上的一条直线垂直，就可以判断AD垂直平面α。你同意他的说法吗？(2)由折痕AD⊥BC，翻折之后垂直关系不变，即AD⊥CD，AD⊥BD，由此你能得到什么结论？

这一铺垫让学生感觉这一判定定理是自己发现的，通过动手、动脑、动口加深了对判定定理的理解。

四、做好解题教学的铺垫，消化例题解题方法

五、做好教学难点的铺垫，降低所学知识难度

铺垫相当于大桥的引桥，给学生以方便，有利于学生更好地学习。虽然不是所有问题都需要铺垫，但对基础薄弱生来说增加铺垫教学还是比较受学生欢迎的。例如“两点间的距离”一节的主要内容是坐标平面两点间的距离公式和用坐标法证明简单的平面几何问题。这节课其中一个教学难点是两点间距离公式推导过程中将两点间的距离化为直角三角形的斜边长度。怎么想到要将两点间的距离转化为直解三角形的斜边长度？突破这一难点可进行如下铺垫：如下图1至图4。

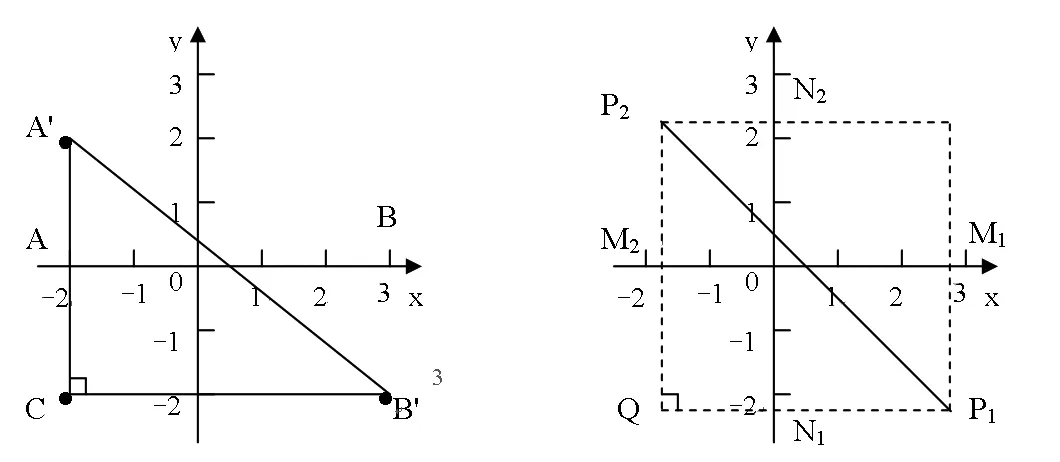
图1 图2

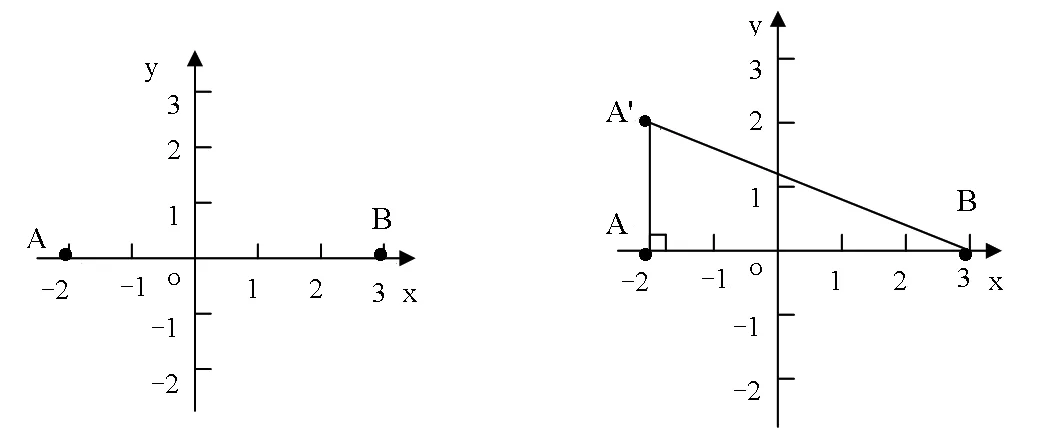
图3 图4

引导学生求横轴上的两点A(-2，0)，B(3，0)间的距离(图1)，然后将A点移到第二象限A′(-2,2)处，再求A′，B间的距离(图2)，之后将B点移到第四象限B′(3，-2)处求A′，B′间的距离(图3)。

学生很容易求出横轴上两点A，B间的距离；当A点移到第二象限时，学生也易看出直角△A′AB，利用勾股定理求出|A′B|；再把B点移到第四象限时，受到第二步的启发，学生可利用勾股定理构造出一个直角△A′B′C求出A′B′间的距离。完成以上铺垫后，教师将A、B两点的坐标改成A(x1，y1)、B(x2，y2)，让学生求A、B间的距离(图4)。这时，学生就容易得出两点间的距离公式。实践证明，这种从特殊到一般，从简单到复杂的铺垫教学是突破教学难点行之有效的方法。

[1]千晓芒.优化课堂教学的五个要领[J].河南教育,1998(8).

2015-01-02

黄清钿(1964- )，男，福建三明人，大田县第五中学高级教师。

G622

A< class="emphasis_bold">文章编号：1673-9884(2015)02-0064-02

1673-9884(2015)02-0064-02