P-理想下半环的新特性

李小光

(西安航空学院 理学院,陕西 西安 710077)

P-理想下半环的新特性

李小光

(西安航空学院 理学院,陕西 西安 710077)

研究P-理想下半环的一些新特性。以P-理想为工具，构造幂等P-理想、素P-理想，半素P-理想，并给出一些新结论，从而定义弱P-正则半环。应用P-理想，研究半环具有的一些新特性，具有一定的实际意义。

全P-幂等半环； 弱P-正则半环；全P-素半环

设(R,+,•)是半环，(R,+)是交换半群，(R，•)是分配半群，存在乘法单位元和吸收零元，则∀a∈R,a•0=0•a=0，a+0=0+a=a。若∀a，b∈R,a•b=b•a，则R是交换半环。若a∈R,∃x∈R,axa=a,则称a∈R是正则的，若半环R中每一个元素都是正则的，则半环R是正则的。若S是一个半环，且半环R的运算在S中封闭，则称半环S是半环R的子集。若A是半环R的非空子集，满足

(Ⅰ) ∀a，b∈R,则a+b∈R;

(Ⅱ)a∈R,r∈R,则ra∈R(ar∈R)

则称A是半环R的左(右)理想。

若A既是半环R的左理想，又是半环R的右理想，则A是半环R的理想。

若I,J是半环R的理想，则I+J={i+j|i∈I∧j∈J}是半环R的理想，且I+J⊂I,J。IJ={∑aibi|ai∈I∧bi∈J}是半环R的理想，且IJ⊂I∩J。若I是半环R的理想，a+b∈I,a∈I,则b∈I,称I是半环R的K-理想。令P+(R)={x∈R|nx=(n+1)x,∃n∈N},则称P+(R)是半环R的理想，但不是K-理想[1]。

定理1[1]若R是半环，令a∈P+(R),∃b∈R,n∈N,满足a+nb=(n+1)b，则b∈P+(R)。

定义1[1-2]设R是半环，I是(左或右)理想,满足

(Ⅰ)∃x∈R,n∈N,则nx+a=(n+1)x；

(Ⅱ)∀a∈I,则x∈I,

称I是R的P-(左或右)理想。

由文献[1]知，P-理想的交集是P-理想，但是P-理想的和不是P-理想。由文献[2]可知，P-理想不是K-理想，一般情况下，K-理想也不是P-理想。

定义2[2]设R是半环，A⊂R,定义

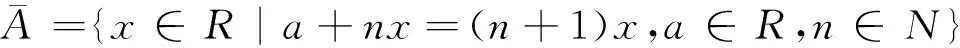
定理2[2]设R是半环，I,J是R的理想，且I是R的P-理想，下面的结论成立：

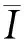
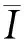
1 素P-理想

定义3 设R是半环，A,B是R的P-理想，A∩B=I，(A∩B⊆I),则A=I或B=I(A=I或B=I)称A是强不可约P-理想。

显然，强不可约P-理想是不可约P-理想。

定理3 设R是半环，I是R的素理想，a∈R,a∉I,则R中存在不可约P-理想H,I⊂H,a∉H。

证明 如果{Hi|i∈Ω}是R中P-理想的链，I⊂Hi，a∉Hi，则∪Hi是R的P-理想，且a∉∪Hi。R的所有P-理想的集合包含I,不包含a，都有一个最大元素H。若H=A∩B,A,B是R的P-理想，则构造H，a∈A,b∈B,a∈A∩B=H,H是矛盾的,因此H一定是不可约P-理想。

定理4 设R是半环，I是R的P-理想，R的所有不可约P-理想的交集包含I。

证明 令{Ai|i∈Ω}是包含I的，是R的所有不可约P-理想族，则I⊆∩Ai。对于反向包含，令x∈R,x∉I,则存在不可约P-理想A，I⊂A,但是x∉A,x∉∩Ai，所以I=∩Ai。

定理5 设R是半环，I是素的P-理想，等价于I是半素P-理想且强不可约。

证明 假设I是R的素P-理想，则I是R的半素P-理想。A,B是R的P-理想,A∩B⊆I,AB⊆A∩B⊆I,则A⊆I或B⊆I,所以I是强不可约的。

相反地，假设I是半素P-理想，且强不可约，AB⊆I,则(A∩B)2⊆AB⊆I,由半素定义可知，A∩B⊆I,由强不可约定义可知，A⊆I或B⊆I,因此I是素P-理想。

2 全P-幂等半环

若半环R的每个理想都是幂等的，则R是全P-幂等半环[3]。

下面，我们定义全P-幂等半环，运用上面的命题描述全P-幂等半环的特性。

定义5 设R是半环，若每一个P-理想是幂等的，则称R是全P-幂等半环。(若I2=I,则称P-理想I是幂等的。)

定义6[1-2]设R是半环，若每一个P-理想是幂等的，则称R是P-正则半环。

定理6 设R是半环，以下结论是等价的：

(Ⅰ)R是全P-幂等半环；

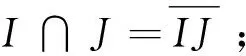
(Ⅲ) 若R是包含单位元1的交换半环，则R是P-正则半环。

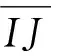
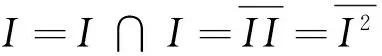
设L是格，∀a,b∈L，∀x∈L满足a∧xb，a∧x包含一个最大的元素C,C称为a相对于b的伪补，格L称为布劳沃格。设LR是一个完备的布劳沃分配格。

以下研究全P-幂等半环R的P-理想格的一些性质。

定理8 设R是全P-幂等半环，P是R的P-理想，则下面的结论是等价的：

(Ⅰ)P是强不可约的；

(Ⅱ)P是不可约的；

(Ⅲ)P是素的。

证明 (Ⅰ)⟹ (Ⅱ)[5-6]，设A,B是R的P-理想，满足A∩B=P,当P是R的强不可约P-理想时，A⊆P或B⊆P,但是P⊆A并且P⊆B,这样A=P或B=P。因此P是不可约的P-理想。

(1)农业资源利用。农业资源包括农业自然资源和农业经济资源，其中农业自然资源是指像土地资源、气候资源、水资源等在农业生产过程中可利用的自然环境因素，农业经济资源是指像交通设施、农业人口、农用机械等在农业生产过程中可利用的社会经济因素。众所周知，我国水资源短缺，且时空分布不均匀，随着农业经济的发展，在农业生产过程中水资源利用率不高、浪费等现象日益明显，水资源污染状况也日益严重。因此，我们要合理高效地利用水资源，本文用各地区有效灌溉面积(千公顷)与各地区耕地面积(千公顷)比值表示农业资源利用，用x1表示。

(Ⅲ)⟹(Ⅰ),令A,B是R的P-理想，满足A∩B=P,由于AB⊆A∩B,因此AB⊆A∩B⊆P。由于P是素理想，因此A⊆P或B⊆P,所以P是强不可约的。

定理9 设P是半环R的包含单位元的P-右理想，则下面的结论是等价的：

(Ⅰ)R是全P-幂指半环；

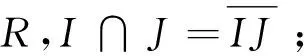
(Ⅲ)R的每一个P-理想都是半素的；

(Ⅳ)R的每一个真P-理想是R的素理想的交。

证明 (Ⅰ)⟺(Ⅱ)，由命题6显然成立。

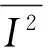
(Ⅰ)⟹(Ⅳ)，由命题4和命题8显然成立。

(Ⅳ)⟹(Ⅲ)，由于素P-理想的交集是半素P-理想，由条件可知，每个P-理想都是半素P-理想。

3 全P-素半环[7-11]

定义7 设R是半环，如果R的每一个P-理想都是素P-理想(半素P-理想)，则称R是全P-素(P-半素)半环。

显然，由命题9可知，全P-半素半环等价于全P-幂等半环。

定理10 设R是半环,R是全P-素半环等价于R是全P-幂等半环，且R的P-理想的集合在包含运算下是全序的。

证明 当R的每个P-理想是素的(半素的)。由命题9，R是全P-幂等半环。令A,B是R的P-理想，当AB⊆A∩B,A∩B是P-理想，则A⊆A∩B或B⊆A∩B。从而A⊆B或B⊆A。这样R的P-理想集合在交运算下是全序的。

[1]P.Mukhopadhyay,S.Ghosh,Anewclassofidealinsemirings[J].SEAMSBull,1999,23(2):253-264.

[2]P.Mukhopadhyay,M.K.Sen,S.Ghosh,p-idealsinp-regularsemirings[J].SEAMSBull,2002(26):439-452.

[3]J.Ahsan,Fullyidempotentsemirings[J].Proc.JapanAcad.1993(69):185-188.

[4]G.Birkhoff,LatticeTheory[M].Publication:Amer.Math.Soc.Colloq,1954:30-50.

[5]BorzooeiRA,ZahediMM.(Anti)fuzzypositiveimplicativehyperk-ideals[J].ItalianJ.PureandAppl.Math,2003,14:9-22.

[6] 王国俊.非经典数理逻辑与近似推理[M].北京:科学出版社,2000:30-50.

[7] 吴忘名.Fuzzy蕴含代数[J].模糊系统与数学，1990,4(1)：56-63.

[8] 谢云鹏.基于包含度的模糊不定性度量[D].西安:西北大学,2008:18-28.

[9] 姚炳学.群和环上的模糊理论[M].北京:科学出版社,2007:84-88.

[10] 戈鲁辛.复变函数的几何理论[M].北京：科学出版社,1956:23-45.

[11] 钟玉泉.复变函数[M].北京：高等教育出版社,2003:72-102.

[责任编辑、校对：周 千]

Semiring Characterized by P-Ideals

LIXiao-guang

(School of Science, Xi'an Aeronautical University, Xi'an 710077, China)

In this paper, the properties of semirings by P-ideals are studied.Through P-ideals, idempotent P-ideals, prime P-ideals and semiprime P-ideals are introduced, and some properties of fully P-idempotent semiring, weakly P-regular semirings, fully P-prime semirings are given accordingly to define weakly P-regular semirings.It is of practical significance to study some new characteristics of semirings.

fully P-idempotent semiring; weakly P-regular semirings; fully P-prime semirings

2015-03-01

陕西省科技厅自然科学基础研究基金资助项目(2013JM1019)；西安航空学院校级科研立项(13XP13)

李小光(1973-)，女，辽宁铁岭人，副教授，从事代数学及信息论方面的研究。

O153.1

A

1008-9233(2015)03-0058-03