一类最值问题的探究与思考

☉浙江省鄞州区正始中学张朱艳

一类最值问题的探究与思考

☉浙江省鄞州区正始中学张朱艳

最值问题是高考数学的常见题型和重要考点·用导数来解决最值问题，是我们熟悉而又常用的方法·但从2015年起，导数退出浙江高考数学的舞台，只在自选模块中考查，这严重阻碍了高考中最值问题的求解·因此，一类不用导数解决的最值问题，应该引起我们的足够重视·

初次见到本题时，学生普遍感觉难度大，无从下手·

其实，在2011年，我们已经接触过非常类似的题目：（2011年高考浙江理科）设x、y为实数，若4x2+y2+xy=1，则2x+y的最大值是_________·

可为什么学生又不会呢？

对于此类最值问题，我们又如何做到举一反三、触类旁通呢？

下面以2011年高考浙江理科的这道题为例，谈谈如何解决这类最值问题·

一、鼓励多解

学生解题时常会按习惯了的单一思路去思考数学问题，高三复习中要鼓励、引导学生从多侧面、多角度思考问题，挖掘问题的实质·

解法2：利用函数思想·

（2x+y）2=4x2+y2+4xy=1+3xy，所以要求2x+y的取值范围，只需求出xy的取值范围·

二、引导多悟

做完试题要及时进行总结反思，因为解题的价值不是答案本身，而在于弄清“问题的本质是什么？”“是怎样想到这个解法的？”“是什么促使你这样想、这样做的？”，这就是说，解题过程还是一个思维过程，是一个把知识与问题联系起来思考、分析、探索的过程·

显然由本题的条件4x2+y2+xy=1，知4x2+xy+y2-1=0.

Δ=12-4×4×1=-15＜0·

所以方程4x2+y2+xy=1所表示的曲线为椭圆，本题的本质为椭圆4x2+y2+xy=1与动直线t=2x+y有公共点，求t的最大值·显然当直线与椭圆相切时，t取得最大值

一道数学试题能否解得顺利，富有创意，甚至正确与否，常常取决于能否发现和利用好题目中的潜在信息·那么潜在信息潜在哪里？又该如何挖掘与利用呢？一般地，（1）信息潜在题设的条件中；（2）信息潜在题设的结构中；（3）信息潜在问题的背景中；（4）信息潜在所求的结论中·

解法1因为发现这是两个变量的和与积关系的最值问题，所以想到了利用重要不等式；解法2因为发现条件和结论中有平方关系，所以想到了利用函数思想；解法3因为发现两个变量问题求最值关键是减少变量，所以想到了利用参数方程；解法4因为发现只是研究与“二次”有关的不等问题，所以想到了“Δ”·

于是，我们不难得出引题的解法·（略）

一题多解的目的是通过思想方法的逐一呈现，从学生最易上手的方式、方法入手，逐步逐级给予引导和批判，不畏艰难，不断优化解题思维品质，从而最终达到提升自身解题的能力·

三、学会多变

在保持问题的本质不变的条件下，适当地改变试题的条件和结论进行变式，利于学生由浅入深地研究问题，利于学生感悟试题考查的知识点，体验数学的本质，彻底地从题海中走出来，从而减轻学生负担，提高学习效率·

基于2011年这道高考题的本质是：圆锥曲线与直线有公共点，求动直线在y轴上的截距，有以下变式·

变式1：设x、y为实数，若4x2+y2+xy≤1，则2x+y的取值范是围是_________·

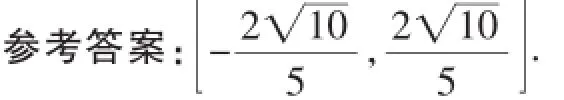
本题的本质是动直线与椭圆所包含的区域有公共点，求参数t的取值范围·

变式2：设x、y为实数，若x2+4xy+y2=1，则2x+y的取值范围是_________·

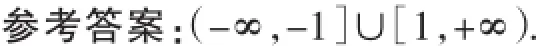
本题的本质是动直线与双曲线有公共点，求参数t的取值范围·

变式3：设x、y为实数，若x2-4xy+4y2+x+y=1，则2x+y的取值范围是_________·

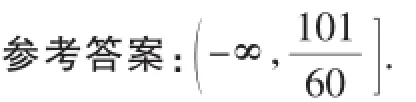
本题的本质是动直线与抛物线有公共点，求参数t的取值范围·

参考答案：［1，+∞）·

变式5：设m、x、y为实数，满足mx+y=5，且4x2+y2+ mxy=1，则m的取值范围是_________·

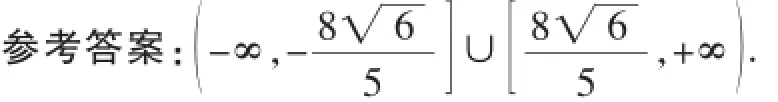
本题的本质是二次曲线与动直线有公共点，求直线方程与二次曲线方程所对应的参数的取值范围·

基于2011年这道高考题的实施方法是：运用重要不等式，有以下变式·

变式6：设x、y为正实数，若2x+y+6=xy，则xy的最小值是_________·

参考答案：18·

变式7：设x、y为正实数，若x+2y+2xy=8，则x+2y的最小值是_________·

参考答案：4·

变式8：设x、y为正实数，若x+3y=5xy，则3x+4y的最小值是_________·

参考答案：5·

对于这一类最值问题的解决，一般有以上几种解法与变式·

同时，我们看到：解题教学的目的是为了培养学生从多角度分析问题，用多途径解决问题的能力；解题教学不能“太匆匆”，对于某些数学问题，教师要通过简明审题来把问题寻解的过程暴露给学生，使学生既“知其然”又“知其所以然”，使学生在遇到相关问题时，能迅速找到解题的突破口·

1·黄加卫·构造性解题方法的几点注记［J］·数学教学研究，2005（11）·

2·刘丹·波利亚数学教育思想对我国数学教育改革的启示［J］·理工高教研究，2003（6）·

3·康武·波利亚与数学教育［J］·中学数学教学参考，1998（5）·A