整体把握教材规划教学核心
2015-05-08江苏省白蒲高级中学丁勇
☉江苏省白蒲高级中学丁勇
整体把握教材规划教学核心
☉江苏省白蒲高级中学丁勇
新课改后,各地涌现出形式各样的教学改革·这些改革涉及了课堂的组织形式、师生地位的重新确定、课堂的教学流程等,一定程度上改观了以往沉闷的课堂,但是这样的改革是表面的、浅层次的,一定时期后,由于教师和学生的“审美”疲劳,不能持续促进提高课堂的有效性·针对上述问题,笔者以为只有从宏观上把握课程核心,对课程内容进行整合、再造,进一步从微观上明晰每一节教学内容的核心,才能使我们的教学有的放矢·本文试图从章节整体把握教材,理解教材,明确本章节最根本、最核心的地方是什么,规划每一节的教学内容,进一步预设出合适的教学形式,使得我们的教学符合学生的认知规律,促进学生的发展,提高教学的效率·下面通过两角和与差的余弦教学案例,阐述笔者的一些思考·
一、章头课——发挥先行组织者的作用,承载知识生成点
案例:两角和与差的余弦·
1·教材内容的分析
微观角度(章节内):本节内容是苏教版必修四第三章“三角恒等变换”第一节内容,通过两角和与差的余弦的学习,进一步学习两角和与差的正弦、正切,以及二倍角的内容·在三角恒等变换的教学中,利用向量的数量积两种运算形式推导出两角差的余弦公式,并以此公式为起点,推导出两角和的余弦公式,进一步推导出两角和与差的正弦、正切,以及二倍角公式·对于学有余力的学生可以在教师的引导下,进行探索和讨论交流,推导积化和差、和差化积、半角公式·新课标与传统教材相比,摒弃把三角变换单纯作为运算,一味强调三角变换的方法和技巧,而关注公式的发现、探索、推导的过程,重视学生思维的培养,关注数学思想的渗透·
中观角度(模块内):必修4共三章内容,三章之间存在紧密的联系·三角变换作为三角函数的运算,是对三角函数知识的进一步运用,另外一方面,三角变换是由三角函数的定义推出的逻辑结论,体现三角函数本质的特征,同时,三角变换中公式的推导,主要借助于同角关系和诱导公式,以及从特殊到一般,再到特殊的数学思想·向量位于本模块的中间章节,充分体现出三角函数与向量的紧密联系,也彰显出向量的双重特性·最显性的是,利用向量数量积推导出三角恒等变换核心——两角差的余弦公式·
宏观角度(模块间):首先,三角恒等变换作为三角函数的运算,不但丰富了三角函数研究的内容,同时又为数学运算家族增添了新成员·其次,三角函数作为特殊的函数有此运算,那么对于后续学习的概率、数列等特殊函数的研究具有指引作用·另外,为数学思想、数学方法的渗透,提供了良好的思维素材·比如化归思想,特殊与一般转化的思想等·
2·教材内容的整合
基于上面教材的解读,我们有必要对相关内容进行整合、再造,确定第一节课,如何体现本节课对本章后续内容的引导作用,发挥先行组织者的作用,如何体现本节课对本章后续内容研究方法的引领作用,如何实现通过本节课的教学促进对本模块内容进一步深化理解,如何有效地把数学思想渗透在思维材料里,通过什么样的方式让学生深刻领会其间蕴含的数学思想和数学方法,从而增长智慧·下面结合具体的教学设计做简要的说明·
3·两角和与差的余弦第一课时教学设计的简要说明
活动目标:
了解两角和与差的余弦公式的推导过程;能用余弦的和差角公式进行简单的三角函数式的化简、求值·
活动方案:
活动一:了解两角和与差的余弦公式的推导过程·
例1设向量a=(cos140°,sin140°),b=(cos25°,sin25°),根据图1,试分别计算a·b=|a||b|cosθ及a·b=x1x2+ y1y2·通过计算你能得出什么结论?

图1
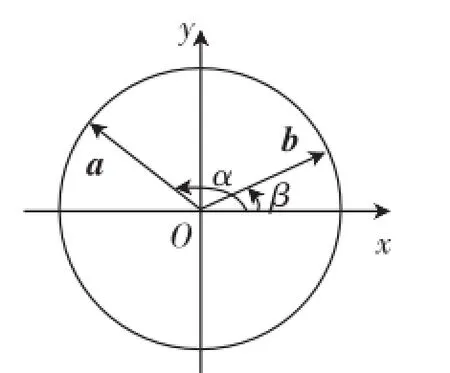
图2
例2若a=(cosα,sinα),b=(cosβ,sinβ),根据图2,你又能得出怎样的结论?
设计意图:首先,给学生指引出发现的方向,可能降低探究的难度,但这种降低是与学生的最近发展区相适切的、是必要的·然后,通过特殊情形,让学生利用向量数量积算两次的方法,得出结论,在此过程中让学生发现运算结果的特征·同时引导学生感受这种发现的一般性,从而进一步推广到一般情形,发现出一般的结论·经历此过程,学生感受与本模块的三角函数的定义、单位圆、和数量积的相关知识建立了联系,同时又是一次知识的应用·最后,让学生体会两角差的余弦的源头是数量积(当然还有其他方法,只是针对本书),体会推导算两次的思想,以及特殊与一般的转化思想·
思考:根据两角差的余弦公式和诱导公式推导出两角和的余弦公式·
设计意图:和与差的运算在其他数学对象中早已经非常熟悉,互为逆运算,如何根据两角差的余弦得到两角和的余弦只是作为学生已有知识、经验在新问题上的应用,另外一方面,我们可以进一步提升对问题的理解,可以把两角和的余弦看成是两角差的余弦的特殊情形,即把两角差的余弦中的β用-β替换·
小结:公式特征·(略)
设计意图:对于数学公式的教学,不但要让学生感受探究的过程,还要对公式的特征加以认识,设计这样的开放小结,让学生发现公式的特征,通过学生的观察,体会出函数名、等式两边的次数、符号、及公式结构等的异同·
活动二:知识运用·
例3利用两角和的(差)的余弦公式证明下列诱导公式:
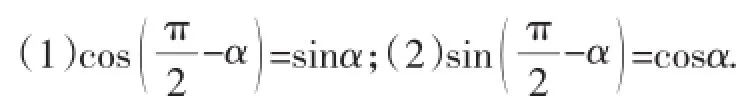
例4不查表,求cos75°,cos15°,tan15°的值·
设计意图:例3(1)通过两角差的余弦公式从另外一个角度认识诱导公式的由来,建立两角差公式与诱导公式的联系,反映出两者的同源性,三角函数的定义·例3(2)蕴含与前面知识及后续知识的联系,一方面与诱导公式的联系,一方面与同角关系的联系,一方面与两角和差余弦的联系,一方面又为本章后续两角和差的正弦做铺垫,是知识的生成点·即与前面知识建立深刻的联系,又为后续知识的生成提供内容和方法·例4通过几个一般角的三角函数值的求法,让学生体会如何处理问题,如何转化的方法·这是三角恒等变换的核心思想和方法之一·通过这两个例题充分彰显三角恒等变换问题的核心方法,同时加强知识间的横向联系,更难能可贵的是加强知识生成点的教学,为后续内容的自然发展,提供了土壤和肥料·当然在解决问题的过程,也体现了许多重要的数学思想·
二、章中课——发挥思维方法的威力,承载知识生长点
波利亚曾经说:“类比是伟大的引路人”·在教学中,通过类比能够引导学生观察对象的相似性,从而提出问题,解决问题·这为我们开展教学提供知识的生长点·比如“等比数列”(第一课时)的教学,学生已经学习等差数列的概念、通项公式、下标和性质,以及前n项和相关内容,那么如何进行等比数列的教学呢·常见的教学方式有以下三种:
方式一:按照等比数列的概念、通项公式、下标和性质,以及前n项和相关内容,按部就班地讲授·
方式二:按照等比数列的概念、通项公式、下标和性质,以及前n项和相关内容,按部就班地讲授·最后利用类比方式比较等差与等比的异同·
方式三:先给出新数列(等比数列),让学生描述新数列的特征,让学生给出新数列的概念(文字语言、符号语言)·进一步说出是怎么给出概念的,学生会回答类比等差数列,自然产生新的问题,等差与等比的异同(文字语言、符号语言)·引导学生思考,给出等比数列的概念后,研究什么内容,你是如何思考的?进一步学生回顾出等差数列研究的内容,说出等比数列研究的内容·再进一步,你能根据等差数列研究内容的结论,猜想出等比数列的结论吗?这是有很大难度的,其实我们需要给学生引导出研究的方法·这时,教师可以做这样的阐述:你能根据等差数列研究内容的方法,类比研究等比数列吗?这样就使得原本冷冰冰的知识,变成学生自主发现、猜想、验证的过程,让学习知识变为水到渠成的过程·
通过上面三种方式的比较,什么样的方式更易于学生主动的学习,答案是显而易见的·而其中最关键的是引导学生发现两类事物的相似性,激发学生类比思维,使得后续知识有知识生长点的指引,但我们还要注意类比的时机,比如方式二、三的差异·上面的案例不仅揭示类比知识,而且类比知识的研究方法,可见类比的强大威力·其实,在高中课程中,这样的类比思维方法,促进知识的生长点还有很多,比如指数、对数、幂、三角函数、数列、概率;椭圆、双曲线、抛物线;线线、线面、面面·在教学中,我们可以借助思维方法,尤其是类比的方法,对于促进学生的学习,培养学生的创新能力有巨大的促进作用·
三、章尾课——重视方法论的力量,承载知识共生点
数学方法论主要研究数学的发展规律、数学思想方法·其主要目标帮助人们学会思维·重视方法论的教学,有利于把数学的学术形态转化成数学的教育形态,有利于学生经历、体会数学家的思维方式,有利于培养学生的创新思维·以“向量数量积”的教学为例,说明方法论教学的重要意义·
运算是数学学习的一个基本内容,运算对象的不断扩展是数学发展的一条重要线索·学生关于数学运算已有哪些知识,有哪些研究的经验?向量对于学生理解数学运算有哪些作用?本节向量数量积的运算有哪些知识,怎么研究,研究哪些内容?其实对于每一种运算,我们都遵循这样的研究方法论:给出运算的定义(有些可以给出几何解释);研究这种运算有哪些特殊的情形(特殊的对象的运算,特殊的位置),比如零元、单位元等(同样可以给出几何解释);进一步研究该运算有哪些运算定律,常见的有交换律、集合律、分配律等,同样对运算定律给出几何解释;最后就是该运算有哪些应用·为了进一步深化对运算本质的揭示,可以从变换、映射、函数的观点认识这些运算,发现运算结构的异同·另外,向量数量积运算的学习既增加运算的内容,又为后续学习其他运算提供方法论经验·使得所有的运算,在运算方法论的大集体中共生·
四、结束语
生成、生长、共生是生物学中的专有名词,反映出生物发展的状态·其中生成、生长反应出个体的发展必经阶段,而共生是反映出两种不同生物之间所形成的互利关系·笔者以为,借助章头课,发挥先行组织者的作用,引导学生找寻知识的生成点,使得知识的学习找到源头,找到知识的“根”;借助章中课,发挥思维方法的威力,引导学生发现知识的生长点,找到知识的“支”,使得知识的生长顺其自然;借助章尾课,发挥数学方法论的力量,引导学生挖掘出知识的共生点,为知识的“根”“支”提供养料·
1·丁非·“活动单导学”模式下的课堂筹划与设计[M]·天津:新蕾出版社,2009·
2·朱占奎·研究整章核心预设内容形式——以高中几何为例谈复习课的整体构想·[J]·中学数学教学参考,2009(11)·
3·郭思乐·改革核心:课程与教学的再造[J]·人民教育,2015(4)·F
