浸润数学文化启发数学思维——“数系的扩充”教学设计

☉江苏省泰兴市第二高级中学丁剑波

浸润数学文化启发数学思维
——“数系的扩充”教学设计

☉江苏省泰兴市第二高级中学丁剑波

一、教材解读

“数系的扩充与复数的概念”是苏教版普通高中数学实验教材选修2-2第三章第一节的内容，课时安排约一课时·复数的引入是中学阶段数系的又一次扩充，引入复数以后，这不仅可以使学生对于数的概念有一个初步的、完整的认识，也为进一步学习数学打下基础·

复数的引入实现了中学阶段数系的最后一次扩充·新课程中复数内容突出复数的代数表示，同时也强调了复数的几何意义·它的内容是分层设计的：先将复数看成是有序实数对，再把复数看成是直角坐标系下平面上的点或向量，最后介绍复数代数形式的加、减运算的几何意义·同时，复数作为一种新的数学语言，也为我们今后用代数的方法解决几何问题提供了新的工具和方法，体现了数形结合思想·通过本节课的学习，一方面让学生回忆数系扩充的过程，体会虚数引入的必要性和合理性；另一方面，让学生理解复数的有关概念，掌握复数相等的充要条件，为今后的学习奠定基础·因此，本节课具有承前启后的作用，是本章的重点内容·

二、教学目标

（1）理解虚数单位等概念；掌握复数相等的充要条件·

（2）由经历解方程的运作领悟引入复数的必要性，在探索复数有关概念中进一步提升合作、交流水平，在定义复数相等的探讨中增强数学转化意识·

（3）在问题情境中了解数系的扩充过程，体会实际需求与数学内部矛盾（数的运算规则、方程求根）在数系扩充过程中的作用，感受人类理性思维的作用，以及数与现实世界的联系·

三、教学流程

活动一：情境引入，再现历史

问题1：1545年意大利数学家卡尔丹遇到如下问题：将10分成两部分，使两者的乘积为40·

设计意图：一方面展示数学家提出的问题，激发学生的学习兴趣；另一方面，引领学生重温历史，感悟数学发现并不神秘，数学家也是从常规问题入手·

问题2：有没有两个数之和为10呢？有没有两个数之积为40呢？为什么刚才的问题无解呢？

设计意图：充分暴露数学家的思维过程，一方面让学生体验数学家的科研精神，另一方面让学生处于“愤悱”状态·

问题3：实数集中有没有这两个数？

设计意图：打破原有认知平衡，形成认知冲突，让学生感受到数已经不够用了，体现学习新知识的必要性·

活动二：设置问题，追溯历史

问题4：数集经历了哪几次扩充？（配图，穿插数的发展史相关知识）

设计意图：学生已经学习过自然数、整数、分数、负数、有理数、无理数、实数等，在此础之上，帮助学生重新建构数集的扩充过程，即自然数集→整数集→有理数集→实数集，这是学生的“最近发展区”，也是本节课知识的生长点·数学典故的讲解可提高学生的兴趣，让学生更加了解数学的本质·

问题5：什么原因导致数的概念逐步扩充的？

设计意图：学生通过回忆、思考每次数集扩充的必要性，解决了哪些问题，即数集为什么要扩充？

让学生感受到这些数的产生不是从天而降，是数学内部发展的需要，也是社会发展的需要·

问题6：如图1，新数集与旧数集是怎样的关系？

图1

（答案：N⊂Z⊂Q⊂R）

问题7：这几次扩充有什么共同的特点？

设计意图：一方面培养学生的观察、概括与表达能力；另一方面通过对前几次数集扩充的梳理，为数系的再一次扩充，以及如何扩充打好了坚实的基础，让学生感受到数系扩充的合理性，并能提炼出数系扩充的一般原则·由此，突破本节课的一个难点·

活动三：还原理论，借鉴历史

然而，历史在前进，社会在发展，生活中的矛盾不断涌现·五百多年前一个怪东西摆在卡尔达诺面前，即-15开平方问题（板书：）·要解决问题，就是要找一个数的平方为-15（板书：（）2=-15=15×（-1））·我们知道，已经解决，因此问题即转化为找一个数的平方为-1？（板书：（）2=-1）

设计意图：教师引领学生再现卡尔达诺问题，将问题转化为找一个数的平方为-1，而且运用规范醒目的板书和留白艺术，给予学生充分思考问题的时间与空间，从而让“引入新数”水到渠成·

问题8：为什么用i呢？是谁引入了i呢？

i是英文单词imaginary（虚幻的）的第一个字母·卡尔达诺当时只是发现了这个矛盾，它的引入者是被称为“分析的化身”的瑞士著名数学家欧拉，引入时间公元1777年，从十六世纪到十八世纪，历史的车轮已经行进了两百多年，可见科学上每一步的迈出是多么的艰辛！

设计意图：教师通过自问自答，介绍与虚数单位i有关的历史，激发学生兴趣，强化对i的认识，并让学生感受到科学上每一步的迈出是多么的艰辛！

问题9：引入i后，你能写出卡尔达诺要找的数吗？

问题10：你还能写出其他含有i的数吗？

问题11：bi与实数a相加的几何意义呢？

复平面上的点（a，b）对应a+bi形式的数，点（a，b）唯一·

设计意图：分别类比实数赋予虚数单位i，数bi和a+ bi的几何表示，使学生更清楚地认识“虚数不虚”，很自然地引出了复数的定义，同时为复数的分类和两个复数相等的条件等知识的出现打下了坚实的基础，同时也为第二节内容做好了铺垫·

问题12：你能写出一个形式，把刚才所写出来的数都包含在内吗？

设计意图：数学需要形式化、符号化·复数的代数形式正是这一体现，也是本节课的重点与难点·笔者通过设计问题9，10，11来铺垫问题12的提出，引导学生由特殊到一般，抽象概括出复数的代数形式，培养学生的抽象概括能力·

问题13：a+bi（a，b∈R）一定是虚数吗？

设计意图：引导学生自然而然地对复数进行分类，攻克本节课的重点·

问题14：虚数与实数构成了一个新的数集，我们把这个新的数集叫做复数集，记作C·这样我们就完成了数系的又一次扩充·我们把新的数系称作复数系·该怎样用描述法表示集合C呢？

（1）复数的定义：（具体内容略）

（2）复数的分类：

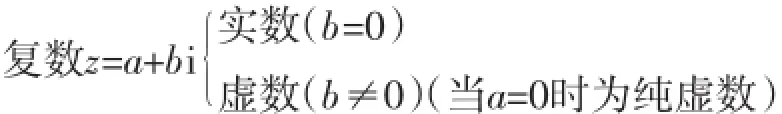
设计意图：通过学生自己动手，合作探究，找到复数分类的标准，解决复数的分类问题，加深对这一知识的理解·

活动四：例题解析，深化概念

例1请你说出下列集合之间的关系：N，Z，Q，R，C·

例2写出下列复数的实部与虚部，并指出哪些是实数？哪些是虚数？哪些是纯虚数？

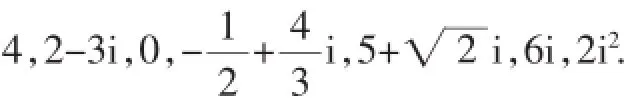
例3实数m取什么值时，复数z=m（m-1）+（m-1）i是：（1）实数？（2）虚数？（3）纯虚数？

例4已知（x+y）+（x-2y）i=（2x-5）+（3x+y）i，求实数x，y的值·

设计意图：例1主要是前后照应，采用概念同化的方式完善认知结构；例2、例3主要是巩固复数的分类标准；例4主要是强化复数相等的充要条件·让学生在解决问题的过程中内化复数的有关概念，起到及时反馈、学以致用的功效·

活动五：反思总结，提炼收获

回顾本节课，i的引入者是欧拉，问题的提出者是卡尔达诺，卡尔达诺虽然没有解决问题，但他依然是大数学家，因为，发现问题比解决问题更重要，哈尔莫斯说过：“问题是数学的心脏·”

四、几点思考

1·浸润数学文化，让学生经历数学知识的发现过程

数学文化，从狭义上说，是指数学思想、精神、方法、观点、语言，以及它们的形成和发展·广义上说，除了上述内涵，还包括数学家，数学史，数学美，以及数学发展中的人文成分、数学与社会的联系等·《新课标》指出：“高中数学课程应该返璞归真，努力揭示数学概念、法则、结论的发展过程和本质·数学课程要讲逻辑推理，通过典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程，体会蕴含在其中的思想方法，追寻数学发展的历史足迹，把数学的学术形态转化为学生易于接受的教育形态·”

本教学设计就是从数学史出发，无论从上课的流程还是问题的设置都尽可能返璞归真，让学生经历数系的发生发展过程·通过对数系扩充的还原，让学生在掌握了知识的同时也获得发现问题、解决问题的能力·数学结论的发现，似乎只是前人的事、数学家的事，不必让学生去寻找，教师也把教学的重心放在结论的应用与巩固练习上·但是，教师应该注意到数学既是一门系统的演绎科学，也是一门试验性的归纳科学，用对数学本质的认识设计自己的教学，力图把“学术形态转化为学生易于接受的教育形态”，有意设计成“研究性学习”，让学生通过实验、观察、探究、归纳，体验数学发现、创造的历程，发展创新意识·

2·改变学习方式，实现以生为本的自主学习

努力改变学生的学习方式，促进学生各方面能力的发展·以人的发展为本，突出学生的发展是《新课标》的基本理念之一·《新课标》“倡导积极主动、勇于探索的学习方式”，指出：“学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式·”

本节课的教学试图努力改变学生的学习方式，以问题串的形式展开，通过数学实验、动手实践、合作交流完成相关问题·学生的参与面较广，参与度较大，积极性很高·整节课学生围绕着数系的发展过程设置问题展开，通过学生独立学习、共同学习，学生的观点得到碰撞，学生的思维得以激发，学生的认知得以提升·在激烈的争辩和思辨中圆满地解决了提出的问题，从中体验了数学发现的快乐，感受到数学的魅力，再现了数学家的思维轨迹，增强了学生自信·教学实践表明，在这样的教学活动中，不仅学生的认知结构得到发展，而且“使学生具有实事求是的态度、敢于探索和创新的精神”，身心与品质也得到发展·

3·教师主导，让学生的思维在问题解决中绽放

扮演好教师在教学活动中的角色·《新课标》指出：“教师不仅是知识的传授者，而且也是学生学习的引导者、组织者和合作者·……在高中数学教学中，教师的讲授仍然是重要的教学方式之一，但要注意的是必须关注学生的主体参与，师生互动·”要改变学生的学习方式，首先教师要改变在教学活动中的角色·数学教学是教师组织下的师生、生生的双边活动·传统意义上的数学教学，往往忽视学生在学习过程中的主体性，忽视学生在课堂上的“参与度”·

本教学设计中，教师通过问题引导，启发学生的思维，引导学生进入知识本质的思考，而且文中问题的设置具有一定的思维容量和梯度性，都能有效地激发学生的思维活动，引导学生有效学习·问题1到3从卡尔达诺第一个研究复数的历史问题入手，再现数学家的思维过程·这样设计在学生思维的“最近发展区”内，具有适切性、联系性、思想性，可引导学生探究发现新知·问题12意在挖掘定义的内涵，界定其外延，通过适当的形式化，反应概念的本质，对提高学生的认识非常有意义·

总之，以学生为主体，教师为主导的教学，教师以组织者、引导者、合作者、促进者的身份捕捉学生的数学心声，点拨探究思路，助燃认知热情，互动双方达成共识，形成共鸣·导学案的教学开放了教学的形式，开放了学习的时间，放开了学生的思维，再现了知识生成的思维轨迹，保障了高效课堂·

1·王振辉，汪晓琴·数学史如何融入中学教材［J］·数学通报，2003（9）·

2·孙庆华·复数的历史发展及在中国的早期传播［J］·西北大学学报，2006（6）·

3·伊夫斯·数学史概论［M］·哈尔滨：哈尔滨工业大学出版社，2009·

4·中华人民共和国教育部·普通高中数学课程标准（实验）［M］·北京：人民教育出版社，2003·F