基于算法思想的解析几何运算策略案例研究

☉江苏省南京市大厂高级中学余建国

基于算法思想的解析几何运算策略案例研究

☉江苏省南京市大厂高级中学余建国

一、提出问题

“提高空间想像、抽象概括、推理论证、运算求解、数据处理等基本能力”是高中数学课程的重要目标之一，也是高考试题的立意所在·在《考试说明》等指导性文件中，对这些基本能力描述得更加具体，如运算求解能力的考查要求是：能够根据法则、公式进行运算及变形；能够根据问题的条件寻找设计合理、简捷的运算途径；能够根据要求对数据进行估计或近似计算·

对照这个考查要求，高考试题中的解析几何解答题显然承载了这项职责·在大部分高考试卷中，解析几何解答题处于中等或稍难的地位，因而是考生志在必得的“得分点”，如2014年高考江苏卷中解析几何题为解答题第3题（共6题），考查椭圆的标准方程与几何性质、直线与直线的位置关系等基础知识，考查运算求解能力·但得分并不理想，满分14分，均分7·6，难度系数0·50·各段得分人数百分比见下表·

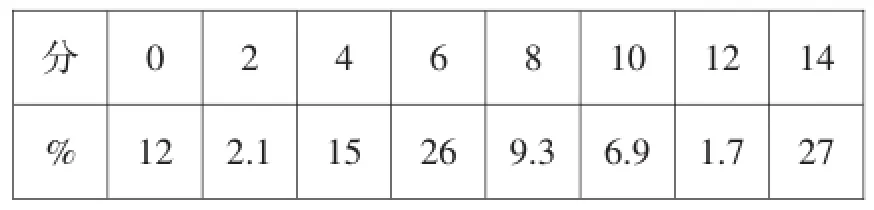
分0 2 4 6 8 10 12 14 % 12 2.1 15 26 9.3 6.9 1.7 27

阅卷反馈的答题状况存在的主要问题是：方法选择呆板、笨拙；运算肤浅、耐力不足，浅尝辄止、半途而废；联想、转化意识欠缺，不能根据现有信息，处理数式·所以，要想在解析几何题上有所突破，提高运算求解能力是突破口·

运算能力的展开基于以下几个方面：算理、算法和数式处理·算理是指在把握问题结构的基础上，从格局上合理布置运算的各个环节，使运算承上启下、有条不紊和结构紧凑，便于运算过程的自然展开；算法是一个将需要引入的运算法则、定理、公式组织成一个紧凑的系统，形成运算的一套程序；数式处理是指相关数（式）的混合运算、变形等实际操作过程·算理、算法与数式处理组成了运算结构的等级层次性，如果将整个运算过程比喻为建造一座大厦，那么其图纸的设计制作犹如算理，采购材料有如算法，砌墙架梁就是数式处理，因此算理对算法与数式处理具有指导作用·我们把算理和算法称为算法思想，在解析几何综合题的运算求解中，缺乏算法思想指导的数式处理是盲目的，因此在复习指导中，应力求在算法思想的层面上指导学生，形成解析几何的运算策略，提高学生的元认知能力·

二、案例解析

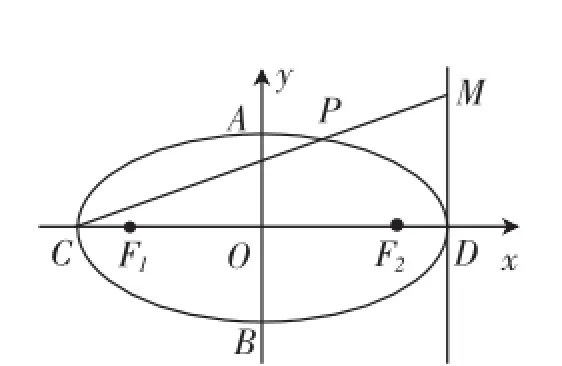
图1

（1）求椭圆的方程·

（2）若C、D分别是椭圆长轴的左、右端点，动点M满足MD⊥CD，连接CM，交椭圆于点P·证明：值·

（3）在（2）的条件下，试问x轴上是否存在异于点C的定点Q，使得以MP为直径的圆恒过直线DP、MQ的交点，若存在，请求出点Q的坐标；若不存在，请说明理由·

算法思想分析：“先动后定”是证明“定值（点）”问题的基本策略，也就是选择合适的自变量t，用t表定值，这其中就需要点P、M的坐标，因此第（2）问的证明可以用流程图（图2）表达·

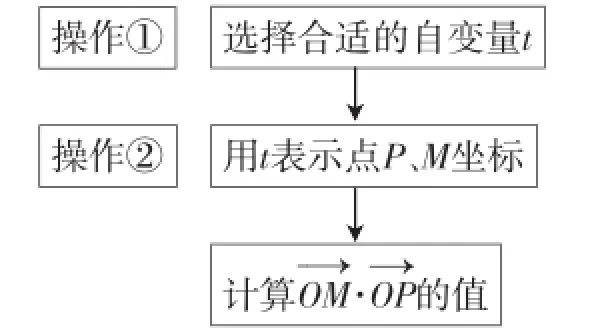
对于操作①，选择谁为自变量呢？审题发现，动点M在直线l：x=2上运动，因此自然地以动点M的纵坐标为自变量·设动点M（2，t），直线MC的方程为x0是这个一元二次方程的两个根，从

对于操作①，动点M在直线l：x=2上运动，等价于“动点P在椭圆上移动，直线CP与l交于点M”，于是我们还可以选择直线CP的斜率为自变量，或者干脆选择点P的坐标为自变量·比较发现，这里的自变量斜率k=因此从本质上看，两种选法核心相同·那么设点P（s，t）为自变量怎么样呢？

算法思想再析：有些省份的高考题刻意回避了韦达定理的使用，这也是新课程的一个特色，尽管还是有很多份高考卷对韦达定理照考不误·因此，对于操作②，如果不用韦达定理，怎么解交点呢？我们以解方程组

在进行梁体浇筑施工时，以施工荷载为依据，结合理论计算挠度来设置合适的反拱，在施工中做好检测工作。以施工方法为依据，对施工荷载及工期进行调整，确定合适的立模高程，保证线形处在要求的范围内。以支架为基础进行施工时，梁体应能产生满足要求的挠度。基于此，为确保支架卸除后可以达到理想的线形，应在施工过程中设置预拱度[3]。

事实上，新课程江苏卷的解析几何解答题（参考答案）总是以这样的方式处理一元二次方程来解交点问题，运算显得简单明了·笔者认为，这么做表面上是回避韦达定理，更重要的是体现了新课程的基本理念，即强调通过基本的数式运算（如分解因式）解决解析几何的运算问题·其算法为：将椭圆方程移项⇒分解因式⇒代入直线方程⇒约分，得一次方程⇒交点的横（纵）坐标·

算法思想三析：再回到操作①的话题·设点P（s，t）为自变量，这就不需要解直线CP（CM）与椭圆的交点了，只需在适当的时候，即计使用（s，t）满足的条们发现，这个程序仍然符合图2所示的流程图·简解如下：

取曲线上的点的坐标为自变量，有时两个动点就有四个字母，看上去字母多了，但如果设计好算法程序，在这个程序的指引下，在数式处理过程中有条不紊地分解、变换、消去等，就能实现目标，此时的算法思想更应清晰、数式处理更应精准，如“点差法”·

有了上面的分析及算法思想示例，我们再来分析解决第（3）问的算法·

算法思想分析：首先，“以MP为直径的圆恒过直线DP、MQ的交点”，解析法是如何对付它的？一种算法是“直译”，将直线DP、MQ的交点坐标代入以MP为直径的圆的方程，通过“恒成立”来确定点Q的坐标（如果存在）；另一种算法是DP⊥MQ，通过斜率或向量建立恒成立的方程确定点Q的坐标（如果存在）·比较而言，由于“转译”了平面几何的相关知识，显然后一种算法更优化，也可用流程图（图3）表示·

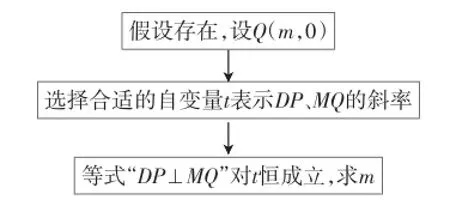
图3

算法思想再析：在解析几何试题中，“运动型”题目既精彩纷呈，也扑朔迷离，但运动与静止是对立统一的，静止是运动的“定格”，运动是静止的“连续”，故动中取静类问题，往往要从“定格”上入手，找出解题的方向·也就是说，先从特殊情形抽象，再一般论证·

三、案例反思

运算求解能力体现在高考命题中具有相对隐蔽性，在命题者的立意中，往往体现得非常明确，但是在命题设计的情境、命题的设问中，都不会明确地提出来·教学过程中，由于一些教师对运算能力的理解不太准确，将其仅仅等同于运算技能，往往将注意力集中在对运算法则的记忆、运算过程的技巧训练上，只追求学生算得又快又对而缺少对运算意义的了解，以及对算理算法的理解和掌握·案例研究表明，清晰的算法思想和对运算过程的预判、调整是提高解析几何解答题运算求解能力的根本·

1·选题要有针对性与研究性

提高解析几何解答题的运算求解能力，例题选择要有一定的针对性、研究性与可拓展性，精心挑选一些具有良好典型性、代表性、迁移性的题目供学生探究，帮助学生从中找出规律与方法，提高运算能力·教师可以从课本上选取或改编例习题，也可以从信度比较高的大市模拟卷中选取，高考题也是不错的选择·笔者提倡从圆锥曲线缤纷多彩的几何性质中，通过特殊化、一般化、类比推广等手段，编制定值（点、线等）类、定性类、最值类等试题，训练学生的解析法思想，提高运算求解能力，这也是圆锥曲线始终作为高考必考内容之一的原因·

2·分析要突出算法思想、画流程图

数学教学中，教师不仅要关注学生能否根据法则、公式等正确地进行计算，更要帮助学生理解运算的算理，将教学重心前移，在审题阶段与学生一起分析题目的条件，寻找合理的、快捷的运算途径，就好比埋头走路前必须抬头看天，先看清楚解题的方向，并且将解题的算法思想用流程图的形式画出来·经过一定量的训练，该类问题的算法思想将内化为学生知识结构中的认知策略，形成认知模式，达到解一题、通一类、带一串的效果·

3·经历运算过程才能培养元认知能力

显然，仅靠一张流程图并不能解决解析几何运算问题·案例表明，自变量的选择、运算路径的设计、遇到困难时算法的调整远比具体的运算技巧，如二元二次方程的变形和分解因式、一元二次方程的韦达定理的应用等更难于被理解和掌握·一个很好的做法是，让学生自己去设计解析几何题的算法思想，当他们碰到困难时给予必要的指导；课堂中展示不同的算法思想指导下的解法，对照比较，取长补短，优化算法·只有经历过程，学生才能真正理解运算的意义和作用，学会从意义的角度预判、调整算法·

例如，2010年江苏高考卷第18题第（3）问：设t=9，求证：直线MN必过x轴上的一定点（其坐标与m无关）·当计学生的做法是先求直线MN的方程，再从方程中找定点·当他们感受过复杂的运算后教师再启发简洁的“先定后动”的算法思想，才能让学生深刻地认识到优化算法思想的重要性，实现比“理解、掌握”更高层次的“评价、创新”的认知要求，发展学生的元认知能力·

当然，运算求解能力与数学的其他能力，如阅读理解、抽象概括、推理论证等紧密联系，也与学生学习数学的情感、态度和价值观有关，所有这方面的能力或实践都得到相应的强化，才能真正破解提高解析几何乃至数学运算求解能力的难题，但毋庸置疑，在运算求解中渗透算法思想不仅是有效的，而且也是新课程的特色和亮点·

1·张昆，许晓天·基于能力立意的高考命题研究——数学高考复习教学设计的视角［J］·中学数学（上），2015（2）·

2·董林伟·倾听学生的思考：例谈运算能力及其培养途径［J］·数学通报，2009（9）·F