直线与椭圆相切问题
——2014年浙江省高考数学理科试题第21题解析
2015-05-08浙江省宁波市北仑职业高级中学徐群
中学数学杂志 2015年9期
☉浙江省宁波市北仑职业高级中学徐群
直线与椭圆相切问题
——2014年浙江省高考数学理科试题第21题解析
☉浙江省宁波市北仑职业高级中学徐群
2014年浙江省高考数学理科第21题如下:
(1)已知直线l的斜率为k,用a、b、k表示点P的坐标;
(2)若过原点O的直线l1与直线l垂直,证明:点P到直线l1的距离的最大值为a-b·
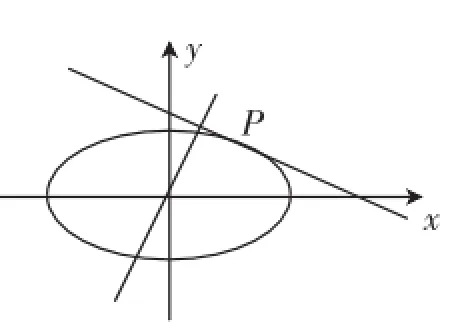
一、解决问题——欲善其事,先利其器


点评:结合导数的定义,利用函数的导数来处理相切问题,求导过程涉及两元函数“隐函数”求导,需要我们用高等数学的观点来处理高中的数学问题·


点评:相比直线与椭圆,直线与圆的相切问题比较容易解决·故考虑坐标变换,将椭圆的方程变成圆的方程来处理·
再探讨(2)的证法·

二、追溯问题——他山之石,可以攻玉
2004年全国高中数学联赛四川省初赛第16题:已知椭圆ξ:=1(a>b>0),动圆τ:x+y=r(b<r<a)·若A是222椭圆ξ上的动点,B是动圆τ上的动点,且使直线AB与椭圆ξ和动圆τ均相切,求点A、B距离的最大值·
三、教学启示——前事不忘,后事之师
重视基础,本题“入口易,深入难”,注重通性、通法,掌握基本概念,强调能力·在日常教学中,不仅要教会学生“怎么做”,更要让学生体会“为什么这么做”·培养学生基本的数学思想,让学生在新课程的教学中,学会自主学习,合作学习·A
