从整体出发认识教材，从认知出发设计教学——以“对数运算”的几种教学设计为例

☉浙江省临海市教研室徐世白

从整体出发认识教材，从认知出发设计教学
——以“对数运算”的几种教学设计为例

☉浙江省临海市教研室徐世白

在台州市高一数学新课程培训会议上，章建跃博士作了题为《注重数学整体性》的专题报告·报告会上，章博士以一种全新的角度对数学的教学方式作了诠释，与会教师都沉浸在章博士的发言之中·笔者也有幸参加了本次报告会，在聆听的过程中，笔者不时有茅塞顿开的感觉·章博士提出的新角度，开拓了笔者对数学教学的思维，令笔者受益匪浅·

章博士提出，整体是事物的一种真实存在形式·数学是一个整体，数学的整体性体现在代数、几何、三角等各部分内容之间的相互联系上，同时也体现在同一部分内容中知识的前后逻辑关系上——纵向联系、横向联系·

数学又是一个系统，理解和掌握数学知识需要系统思维·系统思维就是把认识对象作为系统，从系统和要素、要素和要素、系统和环境的相互联系及相互作用中综合地考察认识对象的一种思维方法·系统思维能极大地简化人们对事物的认知·系统思维给我们带来整体观、全局观·培养系统思维，是为了养成全面思考问题的习惯，避免“只见树木不见森林”，在面对数学问题时，能把解决问题的目标、实现目标的过程、解决过程的优化以及对问题的拓展、深化等作为一个整体进行研究·这样“使学生学会思考，成为善于认识和解决问题的人才”才能落在实处·

但是学生的学习又是循序渐进、逐步深入的，概念要逐个学，知识要逐步教·如何处理好这种矛盾，是教学中的核心问题·以数学知识的发生、发展过程为载体，按学生的认知规律设计教学，使学生经历研究一个数学对象的基本过程，提高发现和提出问题、分析和解决问题的能力，培养认识和解决问题的能力，就显得尤为重要了·然而在实际教学中，不少教师缺乏整体意识和全局观，缺乏对数学系统思维的深刻认识，教学设计往往着眼于点而缺乏全面思考，更有不少教师忽视概念教学，忽视知识的形成过程，把概念教学演绎为解题教学，导致学生对概念生吞活剥，缺乏深刻理解，没法形成知识网络，这对学生的素质培养都是极为不利的·

近期笔者在临海市一所高中调研，听了几节“对数的运算”公开课，感觉几位教师在授课时，大都能把教学重、难点落到实处，但在概念教学中明显缺乏全局观、没有整体眼光，没法从数学的系统性和学生的认知入手设计教学·联系到张博士的整体性思想，感触颇深，特整理成文·

一、教学设计1

师：根据对数的定义及对数与指数的关系，你能解答下列问题吗？

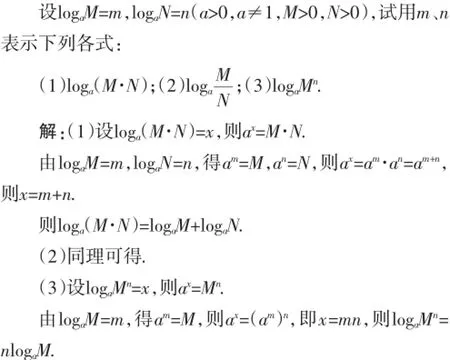
评析：采用这种教学设计的往往是受过老人教教材滋润的教师.以问题形式提出，通过问题解决的方式达到教学目标，是典型的问题式教学法，即教师首先提出问题，学生带着问题自学教材、分析问题、理解问题、讨论问题、解决问题.这种设计看似合理，但关键是问题从何而来.提问是数学教学常用的方式，但问题的提出应合情合理，符合学生实际才不致于突兀.如果问题如同空降，不符合学生的思维发展，学生会惊讶、佩服，会以仰视的目光看待教师的教学，但也会挫伤学生的学习积极性，对学生学习兴趣的培养是无任何裨益的.笔者认为，产生这种教学设计的根源是教师找不到更合理的教学设计而不得已采用的.

也有教师在其基础上作了如下的变式·

师：请研究以下两组对数，思考这三个对数之间有怎样的内在联系，你能得出什么规律？

（1）log232，log24，log28；（2）log215，log25，log23·

由log232=5，log24=2，log28=3，得log232=log24+log28，而三个真数之间满足32=4×8，于是猜测（2）的三个对数间也满足log215=log25+log23，进而在猜测基础上继续教学设计1的教学·

这个变式是为了让问题的提出变得合理，所以从特殊情况入手猜测一般性结果，然后证明，体现了从一般到特殊的数学思想·但问题的提出仍然显得不自然，教师设计过分明显，学生没法理解接受·

另外证明时先设loga（M·N）=x是为了把对数问题化为指数问题进行解决，但不符合学生实际，学生很难想到，不设x则容易出错·笔者在调研中，就曾看到有教师在教学时出现了下面的错误证明：由logaM=m，logaN=n，得am=M，an=N，则loga（M·N）=loga（am+n）=m+n，即loga（M·N）= logaM+logaN·

错误的原因是运用了尚未证明的logaMn=nlogaM·教师尚且出错，学生就不必说了·但如果教师注意到上节课中的练习3、4，并且已经事先落实到位，则最后一步的推理是正确的·这也体现了数学整体性的重要性·如果没有落实到位，也可以令loga（am+n）=x，化为指数ax=am+n，即得正确的推导过程·

二、教学设计2

师：从指数与对数的关系以及指数的运算性质，你能得出相应的对数的运算性质吗？

由于am·an=am+n，设M=am，N=an，于是M·N=am+n·由对数的定义得到logaM=m，logaN=n，loga（M·N）=m+n·这样，我们就得到对数的一个运算性质：loga（M·N）=logaM+logaN·同样可以仿照上述过程，由am÷an=am-n推出logaN·由am=M，（am）n=amn=Mn，化为对数式，得logaMn= mn= nlogaM·

评析：这是2004版人教教材中的引入，由于对数是源于指数，所以教材的设计是从指数的运算来推导对数的运算，体现了将新问题化归为旧问题以及从知识的相互联系性思考问题的想法，较符合整体思想，能体现数学教学的系统思维，而且证明过程也非常流畅.但在实际教学中，发现较少有教师用这种引入方式进行教学，为什么呢？个人感觉从指数运算直接推导对数运算，虽说符合思维发展过程，但本质是综合法思想，推导变形时缺乏目标，看似简单，实则困难.所以不符合学生学习的实际和认知过程，学生不易掌握，估计问题就在此吧.

三、教学设计的再思考

对数在现在的高中数学中处于非常尴尬的地位·在发明电子计算机之前，对数对进行冗长的数值运算是很有用的，它们广泛地用于天文、工程、航海和测绘等领域中·所以恩格斯把对数的发明和解析几何的创始、微积分的建立称为17世纪数学的三大成就，伽利略也说过：“给我空间、时间及对数，我就可以创造一个宇宙·”即使在电子计算机广泛使用的今天，对数的一些重要的性质仍在广泛使用中·但是高中学生感受不到对数学习的必要性和重要性，对学生而言，对数只是必考的知识，所以虽然能勉强对付学习，但时间稍长就什么都忘了·可以说，对数是高中教材中学生掌握得最差且遗忘最快的内容·

那么如何解决这个问题呢？笔者认为，对数的教学更应该注重数学的整体性和系统性，把对数放到一个知识网络中去，让学生在知识的相互联系中理解、掌握、记忆、应用，这才是合理的教学思路·

从整体性、系统性的角度来分析本单元内容·本章首先学习对数，然后学习对数运算，再在此基础上研究对数函数，三者环环相扣·对数源于指数，所以对数的概念教学离不开指数概念，但对数运算的教学直接从指数运算入手就显得有点牵强·所以如上文所述，教师也很少愿意使用教学设计2进行教学·

那么剩下的可能性就是从对数入手研究对数运算了·从数学的整体性和系统性来看，学习了新的数，接下来就要研究它们的运算，所以我们会自然想到两个对数也应该有加、减、乘、除等运算，那么在实际教学中，我们不妨从两个对数的加、减运算着手研究，此时又考虑到对数的底会有所不同，所以先把问题特殊化，考虑同底的两个对数的加、减运算，这样自然把问题引到同底数对数的和、差运算公式的推导上来·即已知logaM、logaN，求logaM+logaN·

由指数与对数的关系，对数问题还是得化为指数进行，所以设logaM=m，logaN=n，有am=M，an=N，运用指数运算法则得am·an=M·N=am+n，化为对数式，得loga（M·N）=m+ n，即loga（M·N）=logaM+logaN（*）·这样推导显然合情合理，符合学生的认知过程，所以教师教得轻松，学生学得自在·同理，设logaM=m，logaN=n，由指数与对数的关系，化为指数式有am=M，an=N，由指数运算法则得am÷an=logaN·把n视为正整数，令（*）中M=N，推广得nlogaM=础上引导学生自主证明，这样也符合学生思维的发展·

按这种思路继续思考，如果对数的底数不同呢？不同底的对数能否化为相同的底呢？自然而然地引入对数的换底公式，设logab=x，则b=ax，取对数logcb=logcax=生认知而一气呵成·

最后，由指数与对数的关系，我们知道指数对应对数、幂对应真数，所以在指数运算中指数相加，在对数运算中应该有对数相加，指数运算中的同底数幂相乘对应对数运算中的真数的相乘；在指数运算中指数相减，在对数运算中应该有对数相减，指数运算中的同底数幂相除对应对数运算中的真数相除；指数运算中幂的乘方对应对数运算中的真数乘方，指数运算中的乘方数与指数相乘对应对数运算中的乘方数与对数相乘·利用这样的联系来引入对数运算的教学，其实也不失为一种合理的教学引入方法，同样符合数学的整体性，但考虑到过分抽象，在实际教学中难度过大，不符合学生的实际，所以可以在完成教学后揭示这种关系，帮助学生形成知识网络，进一步加深理解·

上文所述的几种对数运算教学设计，表面上看，只是同样几个步骤在教学时的不同组合，实质上则是不同教学理念在教学中的体现·在追求教材系统性、整体性的同时，我们还应该考虑学生的接受能力，尽量符合学生的认知，根据学生的认知来设计教学，这样才能真正使学生学会思考，成为善于认识和解决问题的人才·A