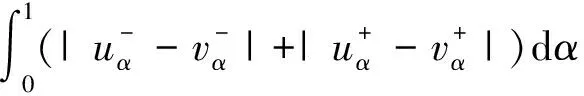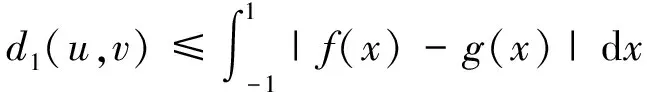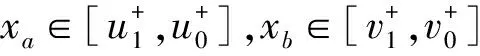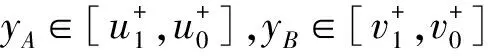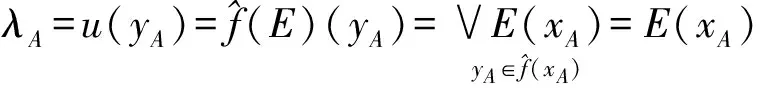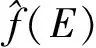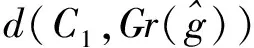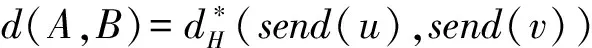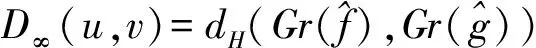模糊数度量的单值函数表示
2015-05-08李雪粉樊太和
李雪粉, 樊太和
(浙江理工大学理学院, 杭州 310018)
模糊数度量的单值函数表示
李雪粉, 樊太和
(浙江理工大学理学院, 杭州 310018)
基于一个具体的三角模糊数作为结构元,给出了模糊数与定义于[-1,1]上的单调递增有界且上半连续的函数构成的集合之间的一一对应关系,从而得到了模糊数的单值函数表示。在上述表示基础上,给出了模糊数空间上的各种度量如上确界度量、Lp度量、sendograph度量的单值函数表现,从而将对模糊数的度量(拓扑)性质的研究完全转化为对普通单调递增有界且上半连续的函数空间中相应性质的研究。
模糊数; 度量; 单值函数; 同胚
1 引言和预备知识
文献[1]提出了模糊数的结构元表示定理,证明了基于一个结构元可以用单调函数表示模糊数。这一表示定理解决了模糊集论中的分解定理、表现定理和扩张原理这三大定理的运用在计算中受参数遍历性限制的问题。本文基于上述表示定理,首先通过固定一个特定的三角模糊数作为结构元,给出了模糊数空间与定义于[-1,1]上的单调递增有界且上半连续的函数集合MJ之间的一一对应;然后基于上述对应给出了模糊数空间上的各种度量如上确界度量、Lp度量、sendograph度量的单值函数表示,从而将对模糊数的度量(拓扑)性质的研究,完全转化为对普通单调递增有界且上半连续的函数空间中相应性质的研究。
本文中I表示单位区间[0,1],J表示闭区间[-1,1],MJ表示定义在J上的单调递增、有界且上半连续的实值函数全体。
定义1.1[2]设u为实数域R上的模糊集,其隶属函数为u(x),如果u(x)满足下述性质:
(1)u是正规的,即存在x0∈R,使得u(x0)=1;
(2)u是模糊凸的,即对于任意的x,y∈R和r∈I,有:
u(rx+(1-r)y)≥min{u(x),u(y)};
(3)u是上半连续的;
(4)u0=cl{x|x∈R,u(x)>0|}是紧致的。
则称u是一个模糊数。
全体模糊数构成的集合记为ε1。

对于任意的A,B∈Rn,A与B之间的Hausdorff距离[2]定义为:

其中
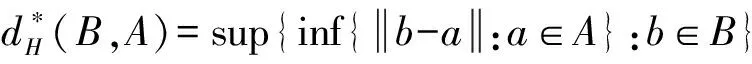
以下是模糊数空间上定义的几个常用度量[2]。
定义1.2 设u,v∈ε1,定义


其中send(u)={(x,α)∈[u]0×I:u(x)≥α}。
则d∞、Lp(1≤p<+∞)和D∞均为ε1上度量,分别称为上确界度量、Lp度量和sendograph度量。
设f∈MJ,如果f是严格单调递增的连续函数,则f的反函数f-1存在并且也是严格单调递增连续函数,而当f不连续时,f不是J到[f(-1),f(1)]的满射,从而f的反函数不存在。为了定义反函数,文献[1]给出了如下延拓反函数的概念。
定义1.3[1]设f∈MJ,f的延拓反函数定义如下:对任意c∈[f(-1),f(1)],

(1) 当y+≤0时,定义f-1(c)=y+;
(2) 当y-≥0时,定义f-1(c)=y-;
(3) 当y-<0 为了下面讨论方便起见,将对定义1.3中条件(3)略作修改,引入下述延拓集值反函数概念: (1) 当y+≤0时,定义f-1(c)=y+; (2) 当y-≥0时,定义f-1(c)=y-; (3) 而当y-<0 容易验证f的延拓集值反函数是定义在[f(-1),f(1)]上的上半连续集值函数。 模糊数的运算是基于扩张原理[3]给出的,但是在利用扩张原理表达问题时,需要对元素遍历某个条件所对应的全体结果进行运算,这种运算中的遍历过程给模糊分析理论带来了极大的不便,使得实际计算和应用时非常不方便。为了克服这一问题,文献[1]中给出了模糊数的结构元表示方法,利用结构元表示有效地克服了这一问题。文献[1]主要定义和结论如下: 定义1.6[1]设A为实数域R上的模糊集,隶属函数记为A(x),x∈R。如果A(x)满足下述性质: (1)A(0)=1,A(1+0)=A(-1-0)=0; (2) 在区间[-1,0)上A(x)是单增右连续函数,在区间(0,1]上A(x)是单降左连续函数; (3) 当-∞ 则称模糊集A为R上的模糊结构元。 如果模糊结构元A分别在(-1,0)和(0,1)上连续严格单调递增和连续严格单调递减,则称A为正则的模糊结构元。 需要说明的是,命题1.1中的结构元和单调函数具有任意性。为了使上述对应确定起见,下面采用固定一个三角模糊数E作为标准结构元,以此标准结构元为基础建立模糊数集合ε1与J上的单调递增有界且上半连续的函数构成的集合MJ之间的一一对应关系,从而使得对模糊数的研究问题完全以一种一一对应的确定方式转化为对普通单调递增有界上半连续函数相应性质的研究。 定义1.7 设E为实数论域R上的模糊集,其隶属函数为 称E为标准三角模糊数。 注:显然,标准三角模糊数是一个正则模糊结构元。以下本文中出现的E恒表示标准三角模糊数。 HM:ε1→MJ, 注:下面给出的证明和[1]中关于命题1.1的证明类似,只不过这里本文构造的函数f是上半连续的。 注:文献[1]中构造的函数f是单调递增且有界的,但是不唯一。在上述定理中,由于要求函数上半连续,从而保证了函数f的唯一性。 在模糊数集合ε1上定义的常见度量有d∞、dp、D∞等度量。关于ε1在这些度量下的拓扑性质的研究是模糊数的基本研究内容。本节中基于上节建立的双射HM讨论模糊数度量空间上不同的度量在MJ中的表现形式,从而将模糊数度量空间的研究转化为对单调递增有界且上半连续的函数类上度量的研究。这就为模糊数度量空间的研究提供了一种新的方法。 首先,因为单调函数是黎曼可积的[4],因此可以在MJ上引入下述定义: 定义2.1 a) 设f,g∈MJ,定义 易知dI和dS都是MJ上的度量[4]。 证明是简单的,从略。 命题2.1说明,若在ε1中定义度量dαI为 则模糊数度量空间(ε1,dαI)与度量空间(MJ,dI)是等距同构的;不难验证dαI和Lp度量拓扑等价,即它们诱导出ε1上相同的拓扑。 例2.1 令 证明:显然,当n固定后fn(x)是单增且有界的。下证fn(x)是柯西列。 不妨设m>n,则 故{fn(x)}是柯西列。 即存在N,当n>N时有 故fn(x)→f(x)。显然f(x)是无界的单调递增函数,这就说明了(MJ,dI)是不完备的度量空间,从而文献[1]中关于(MJ,dI)的完备性结论有误。又由命题2.1知度量空间(ε1,dαI)与度量空间(MJ,dI)是等距同构的,因此模糊数度量空间(ε1,dαI)也是不完备的。 下面研究模糊数度量空间(ε1,dp)与函数类空间MJ的关系,由于Lp与L1具有相同的拓扑性质,在研究(ε1,dp)空间的性质时,只需研究(ε1,d1)即可,有如下命题: 命题2.2 模糊数度量空间(ε1,d1)与度量空间(ΜJ,dI)是度量等价的。 且 又由命题2.1知 故 即 因此,度量空间(MJ,dI)与(ε1,d1)度量等价,从而度量空间(M[-1,1],dI)与(ε1,d1)也是同胚的。 命题2.2说明对模糊数度量空间(ε1,d1)拓扑性质的研究也可以转化为对度量空间(MJ,dI)的相应性质的研究。 以下命题是文献[1]中相应结论的特例。 由HM的双射性及命题2.3可得如下推论: 推论2.1 模糊数度量空间(ε1,d∞)与度量空间(MJ,ds)等距同构,从而同胚。 由推论2.1,对模糊数空间(ε1,d∞)的拓扑性质的研究可以完全转化为J上单增有界且上半连续的函数类相应性质的研究。 本节最后考虑模糊数空间上的sendograph度量在函数类空间MJ上的表现形式。 证明是显然的,从略。 引理2.2 两个不同模糊数之间的sendograph距离的达到点若是在1-截集处,则达到点的的横坐标必为1-截集的端点;即任给u,v∈ε1,u≠v,若a=(xa,λa)∈∂(send(u)),b=(xb,λb)∈∂(send(v)),λa=1或者λb=1 使得 D∞(u,v)=dH(send(u),send(v))=d(a,b), 成立,则有 推论2.2 两个模糊数之间的sendograph距离的达到点若是在0-截集上,则达到点的横坐标必为0-截集的端点,且两个达到点同时为零截集的端点。 这一推论的证明和引理2.2类似,从略。 引理2.3 两个模糊数之间的sendograph距离必然在各自正规点的同一侧达到,即任给u,v∈ε1,必有a=(xa,λa)∈∂(send(u)),b=(xb,λb)∈∂(send(v)),使得 或者 且 D∞(u,v)=dH(send(u),send(v))=d(a,b)成立。 证明:由引理2.1知,必有a=(xa,λa)∈∂(send(u)),b=(xb,λb)∈∂(send(v))使得 D∞(u,v)=dH(send(u),send(v))=d(a,b)成立; 定义2.3 在MJ上定义 易知dHGr是MJ上的一个度量,MJ关于度量dHGr构成的度量空间记为(MJ,dHGr)。 注:利用函数的图研究函数的拓扑性质是点集拓扑学中的常用方法[5]。下述命题给出了模糊数的sendograph度量和与它对应的MJ中表示函数之间度量的关系。 命题2.4 任给u,v∈ε1,E为定义在J上的三角模糊数,且f,g∈MJ,使得 证明:不妨假设 D∞(u,v)=d(A,B),A=(yA,λA)∈∂send(u), B=(yB,λB)∈∂send(v), 且进一步假设 则由扩张原理及f,g为递增函数可知: 且有xA∈[0,1],xB∈[0,1]使得 d(A,D)=d(A1,D1) 这与 矛盾,故 故 从而有 注:命题2.4说明模糊数度量空间(ε1,D∞)与函数类空间(MJ,dHGr)等距同构,从而它们也是同胚的。因此,关于度量空间(ε1,D∞)的研究可以完全转化为对度量空间(MJ,dHGr)的相应性质的研究。 [1] 郭嗣琮. 基于结构元理论的模糊数学分析原理[M]. 沈阳: 东北大学出版社, 2004: 53-96. [2] Diamond P, Kloeden P. Metric Spaces of Fuzzy Sets[M]. Singapore: World Scientific, 1994: 7-70. [3] 陈水利, 李敬功, 王向公. 模糊集理论及其应用[M]. 北京: 科学出版社, 2005: 1-58. [4] 郑维行, 王声望. 实变函数与泛函分析概要[M]. 3版. 北京: 高等教育出版社, 2005: 229-237. [5] Klein E, Thompson Anthony C. Theory of CorresponDences[M]. New York: John Wiley & Sons, 1984: 73-93. (责任编辑: 康 锋) Monotropic Function Representation of Metrics on Fuzzy-number Space LIXue-fen,FANTai-he (School of Sciences, Zhejiang Sci-Tech University, Hangzhou 31800, China) By taking a specific triangular fuzzy number as structural element, this paper gives a bijection between the set of all fuzzy numbers and the set of all bounded, monotonic increasing and upper semi-continuous functions defined on [-1, 1], thus get a monotropic function representation of fuzzy number. On the basis of above representation, this paper gives the monotropic function representation of various metrics on fuzzy number space, such as the supremum metric, theLpmetrics, and the sendograph metric, so as to fully translate the study on metric (topology) properties of fuzzy numbers into the study on the corresponding properties on the space of all bounded, monotonic increasing and upper semi-continuous functions. fuzzy number; metrics; monotropic function; homeomorphism 1673- 3851 (2015) 01- 0135- 05 2014-07-04 国家自然科学基金项目(61170110,11171308,61379018) 李雪粉(1988-),女,河南商丘人,硕士研究生,主要从事不确定性数学理论方面的研究。 O175.14 A


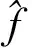





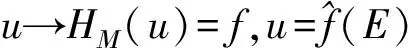


2 模糊数度量的单值函数表示