基于二维测量下的下肢围度拟合研究

庞程方, 任杰文, 倪世明, 夏 馨

(浙江理工大学服装学院, 杭州 310018)

基于二维测量下的下肢围度拟合研究

庞程方, 任杰文, 倪世明, 夏 馨

(浙江理工大学服装学院, 杭州 310018)

采用非接触式人体测量和手工测量两种测量方法来获得人体下肢数据,通过与手工测量方法的比较,发现仪器在围度方向的测量精度受到围度拟合精度的较大影响。因此,本研究通过对下肢的各部位进行分类,并逐类建立回归方程的方法来提高围度的拟合精度,进而提高仪器测量精度。

下肢; 二维测量; 非接触式人体测量; 人体参数

0 引 言

非接触式人体测量是人体测量技术发展的一个大趋势,非接触式测量方法有快速、准确、全面获取人体数据信息等优势,被广泛应用于人体测量与数据采集项目中[1-2]。其中,在二维非接触人体测量系统的开发过程中,如何通过人体的宽度、厚度和高度等已知信息,准确地推算出人体的三围尺寸是二维非接触人体测量系统开发的关键[3]。

中国在二维非接触测量方面的研究起步较晚,但一些科研院校等团队在这方面已获得了一些成果。浙江理工大学在这方面进行了尝试,自主研发了人体下肢二维测量仪并获得了相关专利,它的优点在于简单易行、速度较快。但仪器在数据与手工测定数据的吻合性、围度指标的获取等问题需要做进一步的研究[4]。

1 实 验

1.1 仪 器

人体下肢二维测量仪(绍兴振徳医用辅料有限公司)是自动测量仪,能够自动测量人体下肢数据,方便快速地测量出下肢相关参数。该仪器能快速地测量得到:大腿根下5 cm处高度、围度,腓骨点高、小腿肚围及其对应的围度高和小腿最细处围度,并能对所得数据进行简单的存储、显示等处理。仪器使用CCD摄像机(佳能)拍摄人体正、侧面投影的数字图像,从中直接获取人体高、宽、厚等二维尺寸。而围度尺寸则不能直接获取,必须通过人体的宽度、厚度尺寸及相关指标的信息,间接计算出围度尺寸[3]。仪器的测量系统的如图1。

图1 二维腿部测量系统

1.2 数据预处理

1.2.1 数据采集

随机选取140名身高145～175 cm、体量40～70 kg、年龄18～25岁的青年女性作为被测对象。以人体下肢二维测量仪、皮尺、马丁测量仪等工具对下肢进行测量。

通过仪器测量获得大腿根下5 cm高、腓骨点高、大腿根下5 cm围度、小腿肚围和小腿最细处围度5个项目。

运用手工测量方法进行三次测量,取平均值,得到大腿根下5 cm高和围度、大腿根下5 cm宽度和厚度、腓骨点高、小腿肚围度、小腿肚宽度和厚度、小腿最细处围度、小腿最细处宽度和厚度11个项目。

1.2.2 数据预处理

使用SPSS软件对录入数据进行缺失值、异常个案预处理,删除异常和重复个案数据,作出各部位尺寸的茎叶图和箱型图,找出含有奇异值的样本,并进一步剔除这些样本的数据。根据检验,剔除了14个样本,余下126个样本进行后续处理,通过正态性检验,剩下的126个样本测量数据符合正态性分布,能够进行接下去的仪器测量数据与手工测量数据差异性分析、各变量之间的相关分析和回归分析。

2 数据分析与讨论

2.1 仪器的精度检验与误差分析

将仪器测量值与手工测量值进行比较,分析二维腿部测量系统的精确性,如表1。

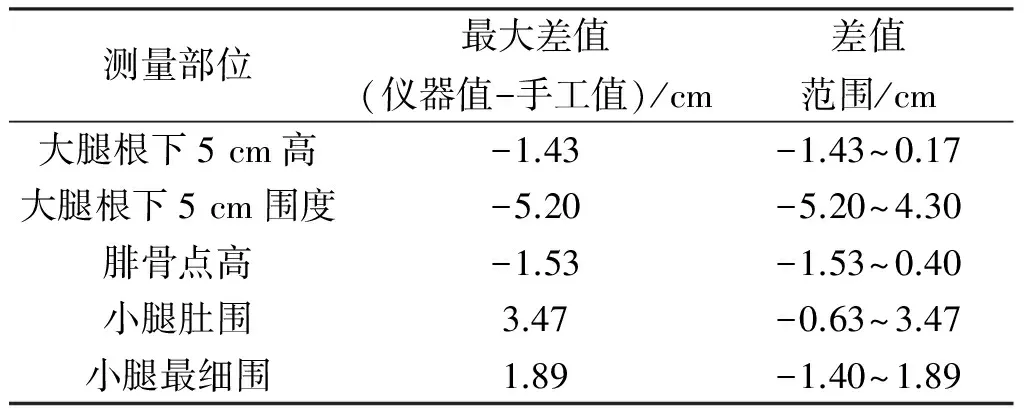
表1 仪器测量数据与手工测量数据的最大差值、差值范围

由表1可以看出,仪器在高度方向的测量值与手工测量值的偏差值在-1.43～0.17 cm与-1.53～0.40 cm之间,基本满足GB/T 1335.2—2008《国家服装号型》标准中规定的成年人体尺寸误差在-1.5～1.5 cm的要求[3,5],而仪器在围度方向上的测量值与手工测量值的偏差值超出了服装业生产中的要求。

2.1.1 差异性检验

将仪器测量数据与手工测量数据进行均值差异性比较,从而验证仪器测量获取数据的可靠性[6]。本文选定大腿根下5 cm处高度和围度、腓骨点高、小腿肚围和小腿最细处围度5个指标,均值比较结果见表2。

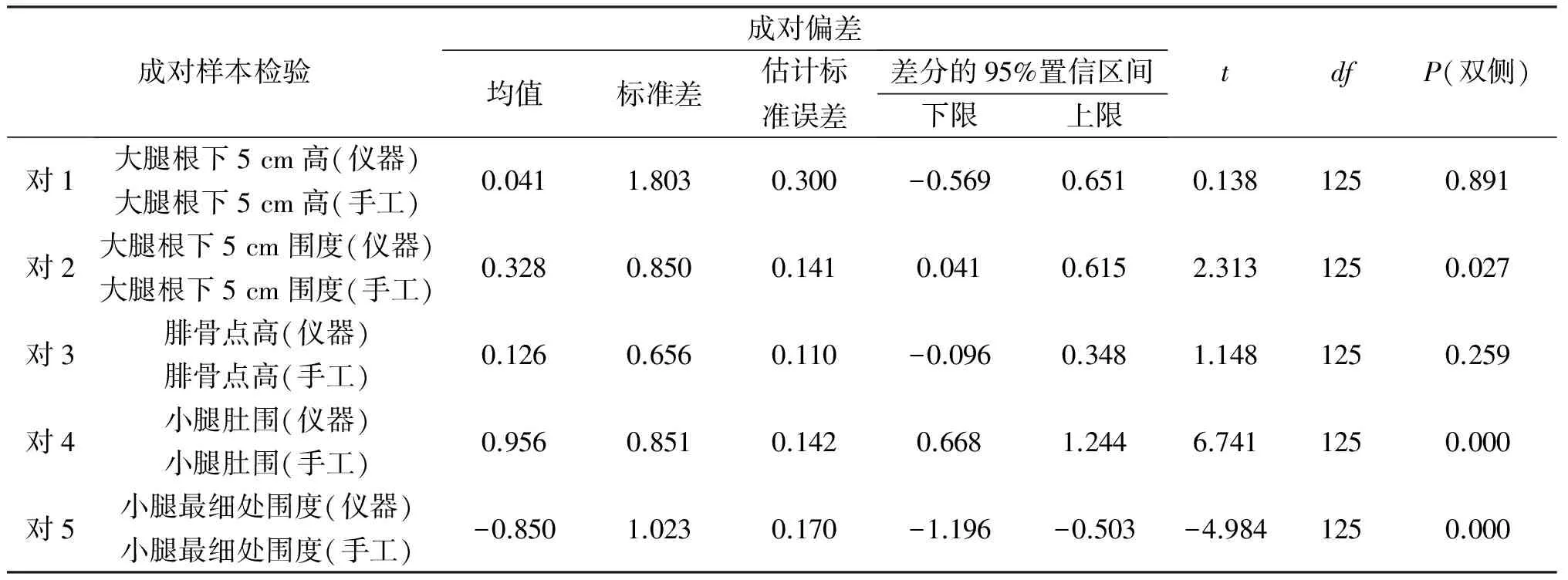
表2 腿部特征部位尺寸配对样本t检验

分析表2可知,大腿根下5 cm高、腓骨点高的P(双侧)都大于0.05,说明测量值与实际值均值之间有无显著差异;而大腿根下5 cm处围度、小腿最细处围度、小腿肚围的测量值均值与实际值均值之间存在显著差异。仪器测量在高度方向的尺寸是采用直接对图片像素进行换算得来,相对围度方向的尺寸来说精确度较高;围度方向尺寸是通过对图片像素换算后再间接拟合得到,测得的尺寸与手工尺寸有显著差异,因而需要对围度上的拟合精度进行改进。

2.1.2 误差产生原因分析

通过与手工测量数值的比较可以发现,仪器测得的尺寸在高度方向上存在的误差主要由仪器本身存在的系统误差所产生,其误差范围在服装生产可接受范围内;而在围度方向上的误差主要由于间接拟合计算所造成的,其误差范围远远超出服装生产的要求,因此需要对围度的拟合模型进行改进,从而提高围度方向的测量精度。

手工测量数据与仪器测量数据之间的误差产生原因主要是仪器围度拟合误差,拟合误差是指曲线拟合时产生的误差,拟合效果好坏直接影响结果精确度。由于仪器测量系统中的围度进行拟合时,将整个样本库作为一类进行拟合,并未考虑人体腿部形态多样,从而造成个别样本在测试时出现较大的尺寸偏差。因此,为增强围度尺寸预测的精确度,减少模型内部不确定因素,可将人体腿部形态进行分类,分别建立预测模型[7]。

2.2 仪器拟合精度的改进

实验最终得到有效样本126个,随机抽取120个样本进行分类和模型建立,剩余6个作为验证样本。

2.2.1 相关性分析

分别将三个围度与对应的宽度和厚度进行相关性检验,结果见表3。

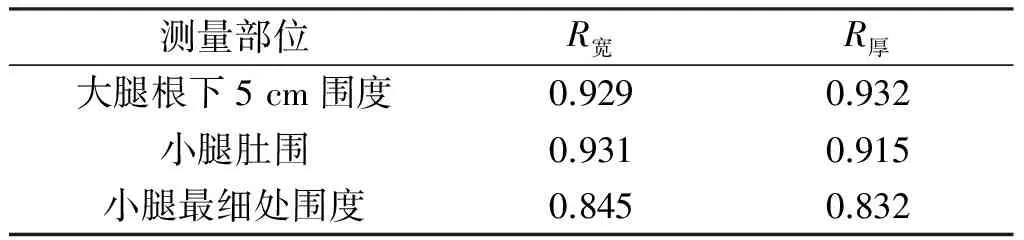
表3 各个围度与相应变量之间的相关分析

通过表3可知,下肢各个围度与其对应的宽度和厚度有高度相关性,因此本文通过宽度和厚度拟合出下肢各部位的围度。

2.2.2 下肢分类

为提高系统测量精度,引入横径矢比(横径矢比指的是宽厚之比,用横径矢比来表示大腿根部、小腿肚和小腿最细处横截面的扁平程度)将下肢进行分类,分别建立预测模型。考虑到选取的分类间隔过大时,易造成分类类别的样本数过于集中某一区间;而分类间隔过小时,将导致各类别的样本数量过于分散,不利于建立回归方程。因此,将特征部位横截面横径矢比以0.05为间隔分成四档。在这里,引入身体风格的特征系数概念,它表示宽度和厚度值比[8],用符号“D、X、H”分别代表大腿根下5 cm处、小腿肚围、小腿最细处横径矢比。

运用SPSS软件对数据进行升序排列,然后以0.05为间隔进行分类，结果如下表4。

表4 根据横径矢比对围度分档

由表4可以看出，D1、D4、X1三类中样本数较少,满足不了围度拟合的样本要求,据相邻原则予以合并,将D1类并入D2类,D4类并入D3类,将X1类并入X2类。则大腿根下5 cm围分为D2、D3两类;小腿肚围分为X2、X3、X4三类;小腿最细围分为:H1、H2、H3、H4四类。

2.2.3 拟合方程的建立

通过相关性分析得出下肢围度和宽、厚之间都是线性相关,相关关系显著。因此,运用逐步回归分析对每一类建立拟合效果最好的回归方程为:

D2:大腿根下5 cm处围度=3.761+2.786×大腿根下5 cm厚+0.121×大腿根下5 cm宽;

D3:大腿根下5 cm处围度=7.873+2.694×大腿根下5 cm宽;

X2:小腿肚围=9.356+2.312×小腿肚宽;

X3:小腿肚围=5.356+2.239×小腿肚宽+0.290×小腿肚厚;

X4:小腿肚围=-2.650+3.500×小腿肚宽;

H1:小腿最细处围度=4.384+3.318×小腿最细处宽;

H2:小腿最细处围度=1.349+2.740×小腿最细处厚;

H3:小腿最细处围度=-11.363+4.051×小腿最细处厚+0.071×体重小腿最细处厚;

H4:小腿最细处围度=3.112+3.190×小腿最细处宽。

2.2.4 回归模型验证

如表5所示,各类围度在拟合时的相关系数,判定系数,调整的判定系数较大,而回归估计的标准误差较小,这说明样本的回归效果较好。

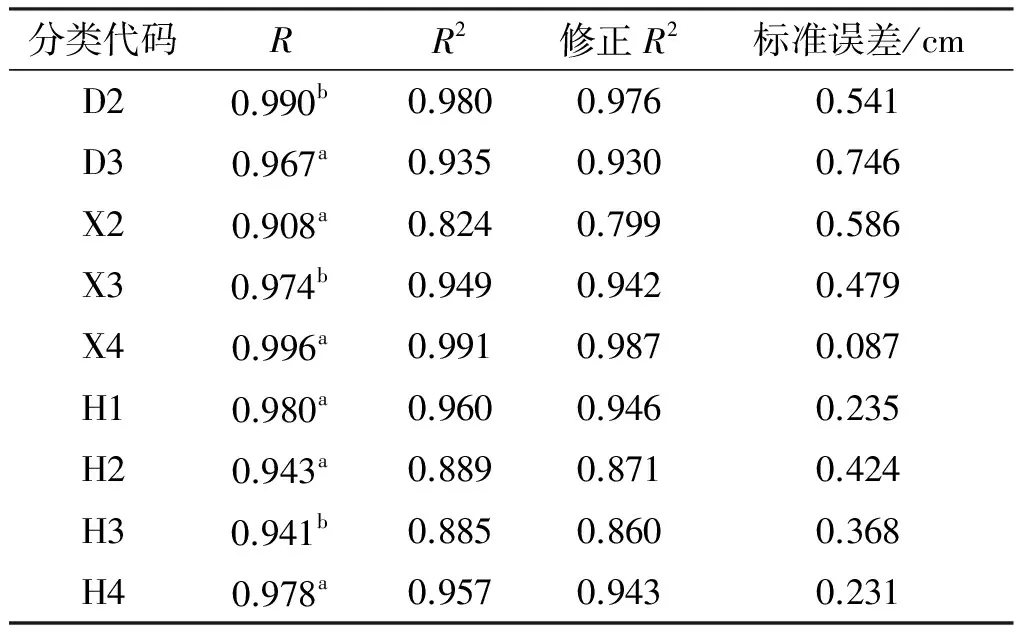
表5 各类别围度的拟合模型概况

将随机抽取出的6个样本按照各尺寸部位的类别代入相应的回归方程计算结果,与手工测量值进行比较,分析计算值与手工值之间的差异是否显著。验证结果如表6所示:

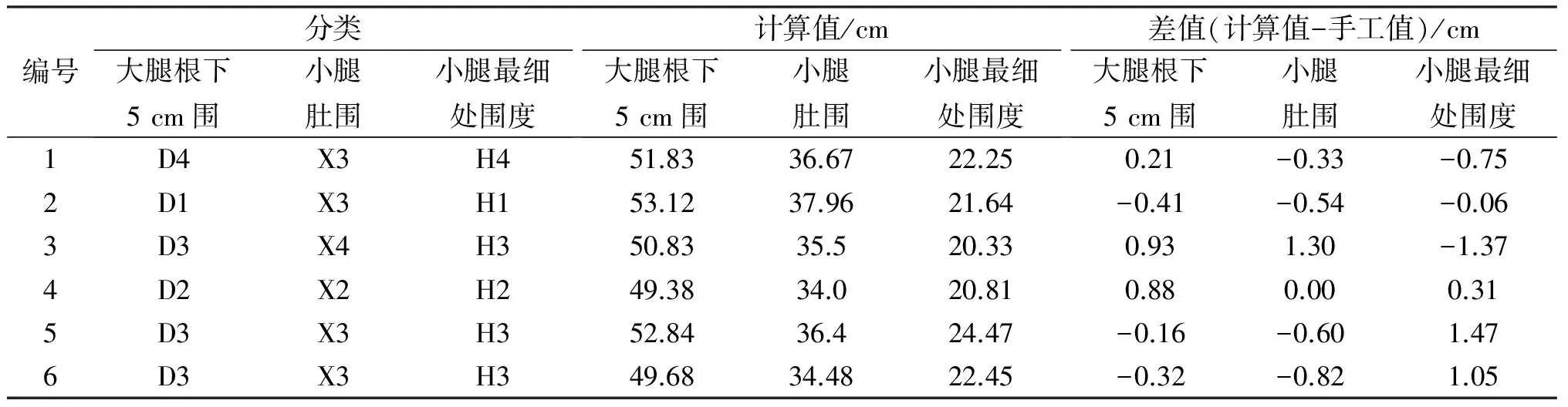
表6 验证样本的腿型分类及回归方程预测结果分析

由上表可以看出,回归方程计算结果与实际值之间的绝对差异较小,两者差值范围在-1.37～1.47 cm,满足服装尺寸误差在-1.5～1.5 cm的要求。与改进前相比,大腿根下5 cm的围度误差范围由-5.20～4.30 cm变为-0.41～0.93 cm,误差范围缩小8.16 cm,测量精确度提高85.89%(误差范围缩小值/原先误差范围值);小腿肚围的误差范围缩小1.98 cm,测量精确度提高48.29%;小腿最细处围度误差范围缩小0.45 cm,测量精确度提高13.68%。

3 结 论

通过对人体下肢二维测量仪器的精确度进行验证,发现二维测量仪在高度方向上的测量精确的较高,而围度受到间接计算的影响,通过拟合得到的尺寸偏离服装生产的基本要求。通过对反映下肢截面形态扁平程度的横径矢比进行分类,将腿部围度上的形态进行区分,将大腿根下5 cm处的腿部形态分为D2、D3;将小腿肚围处的腿部形态分为X2、X3、X4;小腿最细处的腿部形态分为H1、H2、H3、H4四类。

根据各部位所类别,逐类建立相应的回归方程来计算围度尺寸。通过验证,改进后得到的下肢围度计算值与手工测量值的偏差范围在-1.32～1.47 cm之间,大腿根下5 cm的围度测量精确度提高85.89%;小腿肚围的测量精确度提高48.29%;小腿最细处围度的测量精确度提高13.68%,测量得到的各个尺寸数据满足服装生产的要求。

[1] 潘 力, 王 军, 姚 彤, 等. 接触与非接触式人体测量数据比较[J]. 大连工业大学学报, 2012, 32(2): 140-142.

[2] 王 星, 王兆青, 李蒙龙. 基于参照法的人体测量的误差分析[J]. 工业控制计算机, 2012, 25(8): 108-109.

[3] 中国服装工业总公司. 国家标准《服装号型》的说明与应用[M]. 北京: 中国标准出版社, 1992: 1-15.

[4] 葛 彦, 刘国联. 用于服装业的照相人体测量方法研究[J]. 纺织学报, 2007, 28(10): 78-81.

[5] 李晓久, 王玉秀. 二维非接触式人体测量系统中臀围的计算[J]. 纺织学报, 2004, 25(2): 98-99.

[6] 张益洁. 女性腿部形态分析与尺寸模型的研究[D]. 杭州: 浙江理工大学, 2012.

[7] 王玉秀, 李晓久, 刘 皓. 二维非接触人体测量中体型的模糊聚类分析[J]. 纺织学报, 2007, 28(2): 100-103.

[8] Kong H Y, Gu B F, Gu P Y, et al. Calculation rules research of female lower body torso 3D sizes[J]. Procedia Engineering, 2011(15): 4326-4330.

(责任编辑： 杨一舟)

Study on Circumference Fitting of Lower Limbs Based on Two-Dimensional Anthropometry

PANGCheng-fang,RENJie-wen,NIShi-ming,XIAXin

(School of Fashion Design and Engineering, Zhejiang Sci-Tech University, Hangzhou 310018, China)

This paper adopts the non-contact anthropometry and manual measurement to obtain the data of lower limbs. Compared with the manual measurement method, it is found that the measurement accuracy of the instrument is greatly influenced by circumference fitting accuracy at circumference direction. This study improves circumference fitting precision and then boots instrument measurement accuracy through classifying each part of lower limbs and establishing regression equations according to the classification.

lower limbs; two-dimensional anthropometry; non-contact anthropoment; human parameters

1673- 3851 (2015) 01- 0051- 04

2014-03-12

浙江理工大学研究生创新研究项目(YCX13016)

庞程方(1989-),男,浙江台州人,硕士研究生,主要从事人体工程与数字服装方面的研究。

夏 馨,E-mail:29810868@qq.com

TS195.644

A