基于小波包－AR谱和支持向量机的连杆轴承故障诊断

常 春，王国威，梅检民，张玲玲，郭 正

(1.军事交通学院研究生管理大队，天津300161;2.军事交通学院军用车辆系，天津300161)

连杆轴承是发动机的重要部件，其状态的好 坏直接影响发动机的技术状态，及时发现并诊断连杆轴承故障对发动机安全运转具有重要意义。发动机壳体振动信号往往包含有丰富的故障信息，连杆轴承特征微弱，容易被发动机其他振动和噪声淹没，因此，要实现连杆轴承故障诊断，需要研究有效的特征提取和故障诊断方法。

对于往复式发动机连杆轴承异响故障的研究，国内外许多学者已经进行了较为深入的工作［1－4］，主要是采用振动分析方法，针对发动机缸体表面振动信号，使用不同的信号处理和模式识别方法进行故障诊断。

发动机振动信号具有非平稳和非线性特点，信号中还包含多激励源和噪声干扰，要从中剥离出特征信息，需要有效噪声抑制和特征提取方法。小波包能将信号进行多层次划分，自适应地选择相应的频带匹配信号特征，将包含特征信息的信号和其他信号分解在不同的频段中［5］，实现了特征信号与干扰信号的分离，但要准确识别哪些频带包含了主要特征信息，需要对小波包分解后的各频段信号再进行特征提取分析。自回归(auto regressive，AR)谱是基于参数建模的功率谱估计，相比经典功率谱具有更好的频率分辨率，适合分析短样本信号，对观测数据具有外延特性，非常适合对小波包分解的频率信号进行深入细致分析。

支持向量机(support rector machine，SVM)作为一种结构风险最小化的机器训练和模式识别方法，能实现小样本准确模式识别，具有直观的几何解释和良好的泛化能力，已经成功应用于机械故障诊断、图像识别等分类问题［6］，而选择有效的特征向量作为支持向量机的学习样本是影响SVM分类性能的重要因素［7］。

本文以东风EQ6BT型柴油发动机连杆轴承故障诊断为研究对象，对3种不同磨损状态的连杆轴承振动信号进行小波包分解，重构各频段信号并分别进行AR谱估计，提取不同频带的小波包－AR谱能量，将不同位置不同频段能量输入支持向量机，建立SVM多分类器，对正常与多种故障状态进行分类，取得了良好的效果。

1 小波包-AR谱和SVM诊断方法

1.1 小波包分解与重构

小波包分解实质上对检测信号进行多通道滤波，通过不同频率的小波与检测信号相互作用，将信号划分成不同的频段，减少信号间的干扰。同时，小波包分析能够根据被分析信号的特征，自适应地选择相应频带，使之与信号频谱相匹配，从而提高时频分辨率。因而，小波包分析更适合对信号进行时频分析，可用于分析复杂的往复机械故障特征［8］。

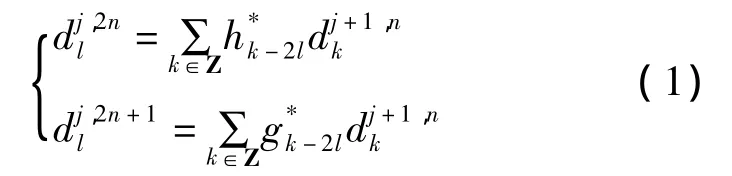
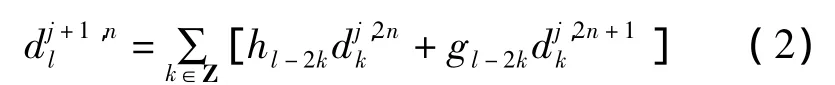
式中:hl－2k、gl－2k分别为小波包重构的低通、高通滤波器组。

以3层小波包分解重构为例，将故障信号S进行3层小波包分解，分别提取第3层从低频到高频成分的信号特征;小波包分解系数为X30，X31，…，X37。(0，0)节点代表原始信号 S;(1，0)代表小波包分解的第1层低频系数X10;(1，1)代表小波包第1层的高频系数X11，以此类推。对小波包分解系数重构，提取各频带范围的信号。S30表示X30的重构信号，S31表示X31的重构信号，其他类推。则原信号S可表示为S=S30+S31+…+S37。

1.2 AR 谱估计

信号仅通过小波包分解难以得到希望的结果，需要进一步采用其他的方法进行分析。信号的谱估计主要有参数模型法和非参数模型法两类，AR谱估计是参数模型法中最广泛的一种方法，其谱峰尖锐，频率定位准确，易反映功率谱中的峰值信息。AR谱估计的基本思想是先对时间序列信号建立AR模型，再用模型系数计算信号的自功率谱［9］。

AR(N)模型的一般表达式为

式中:x(n)为自回归时间序列;u(n)为具有零均值、方差为的正态分布有限带宽白噪声;ak为回归系数;N为模型的阶次。

如果将式(3)看作一个系统的输入/输出方程，则u(n)可视为系统的白噪声输入，x(n)为系统在有限带宽白噪声激励下的相应输出。

根据自谱的定义，利用传递函数可求出信号的单边谱为

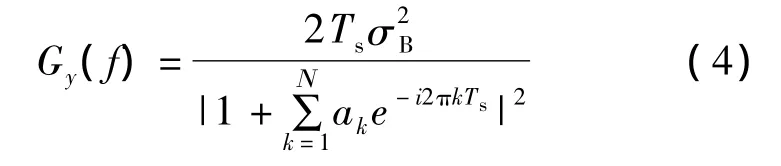
式中:取 f∈［0～fs/2］(一般取 f∈［0～fs/2.56］);Ts=1/fs，fs为采样频率。

1.3 SVM 原理

支持向量机由Vapnik首先提出，它的主要思想是建立一个分类超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化。SVM［10］将向量映射到一个更高维的空间里，在这个空间里建立一个最大间隔超平面H。在超平面H的两边建立两个互相平行的超平面H1、H2。平行超平面间的距离越大，分类器的总误差越小。图1为SVM分类示意，H1、H2上的样本为支持向量。寻找最优分类面的问题可转化为

式中:ω为分类超平面的权系数向量;Φ(·)为从低维空间向高维空间的线性映射;c为惩罚因子;ξi为松弛变量。

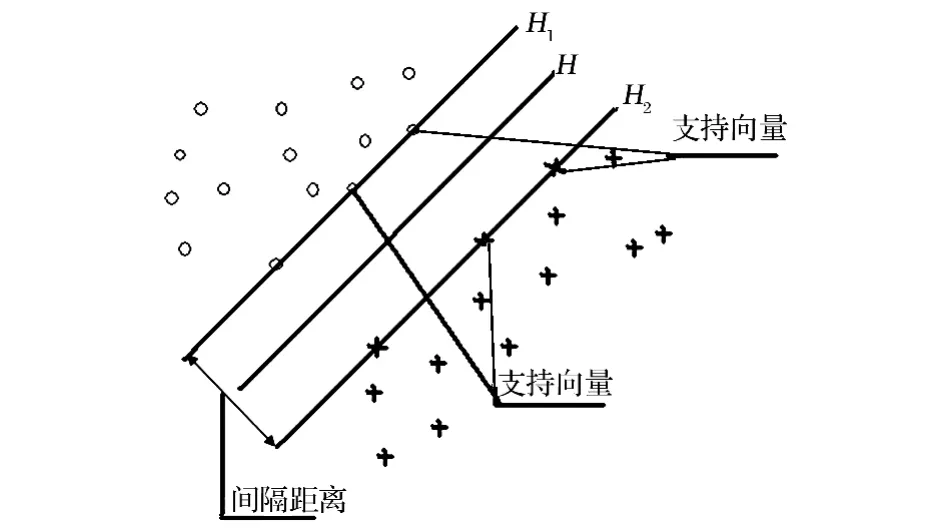
图1 支持向量分类示意

利用拉格朗日乘子法，并引入核函数，问题转化为

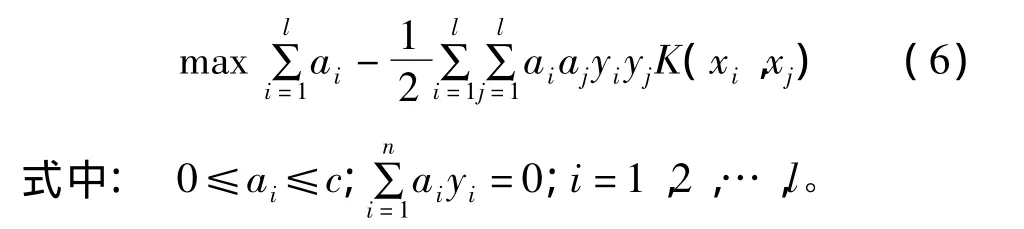
核函数取径向基函数:

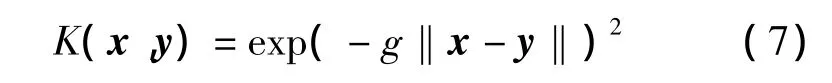
式中ai为拉格朗日乘子。

核函数中参数g的取值对模型的分类精度有重要影响。惩罚因子c用于控制模型复杂度和逼近误差的折中，c越大则对数据的拟合程度越高，但泛化能力将降低。通过求解可得ai，进而求得ω和b，从而确定分类超平面。

SVM采用一对一的思想实现多分类，采用k组交叉验证(k－fold cross validation，k－CV)的思想进行训练，将数据分成k组，每组分别做一次测试集，其余作为训练集，这样得到k个模型，用这个模型分类准确率的平均值作为k－CV下分类器的性能指标，此处取k=3。

1.4 诊断流程

基于小波包－AR谱和SVM的故障诊断方法首先将发动机连杆轴承振动信号进行小波包分解，重构各频段信号并进行AR谱分析;然后累加不同频段的能量实现连杆轴承故障特征提取，将提取的特征作为输入向量对SVM多分类器进行训练;最后将待测样本的特征值输入SVM，即可实现正常状态与故障状态的识别。该方法的实现流程如图2所示。

图2 基于小波包-AR谱和SVM的故障诊断方法

2 连杆轴承故障诊断实例分析

2.1 试验

以东风EQ6BT型柴油发动机作为试验对象，选择第3缸连杆轴承为故障轴承，分别设置连杆轴承的配合间隙为0.08 mm(正常间隙)、0.20 mm(轻微磨损)、0.40 mm(严重磨损)。

图3给出了试验装置结构图，上位机采用NI PXI－1044计算机，配有PXI－6221数采卡实现A/D转换和数据采集功能，振动传感器采用IMI 601A11传感器，转速传感器采用霍尔传感器。转速监测装置与A/D转换器构成非稳态信号采集器，与传感器、上位机构成信号采集系统。其工作原理是下位机加电后，发动机转速监测模块开始工作，监测发动机转速，当发动机转速达到预先设置的起始转速时，开始根据预设的采样频率和采样点数采集发动机振动信号，并将振动信号保存到上位机中。

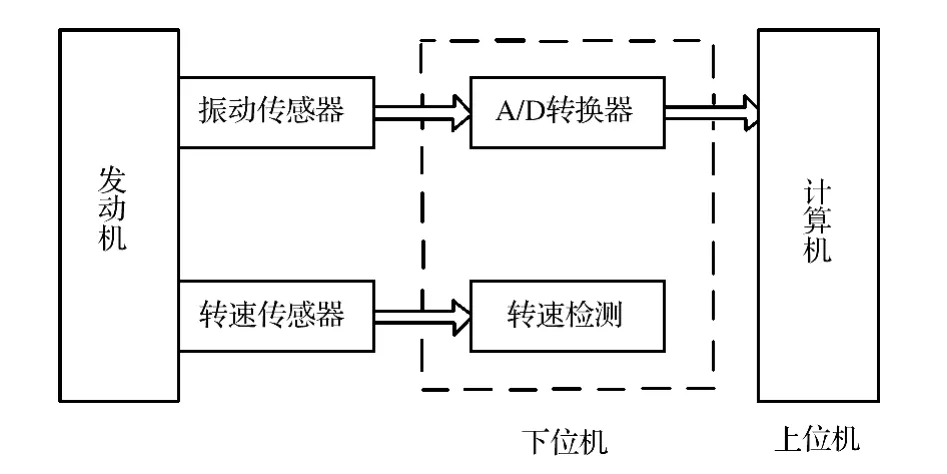
图3 试验装置结构示意

文献［11］指出，连杆轴承的最佳诊断部位为发动机缸体—油底结合左右侧和油底下部，故将振动加速度传感器分别放置在3个最佳诊断部位:A——油底与缸体接合处第3缸右侧;B——油底与缸体接合处第3缸左侧;C——第3缸油底下部。测量发动机运转时的振动信号。

在柴油机转速为1 300 r/min时采集试验数据，采样频率为25.6 kHz，采集了前述3种技术状况下的发动机振动信号，位置A处3种技术状况下的振动信号如图4所示。

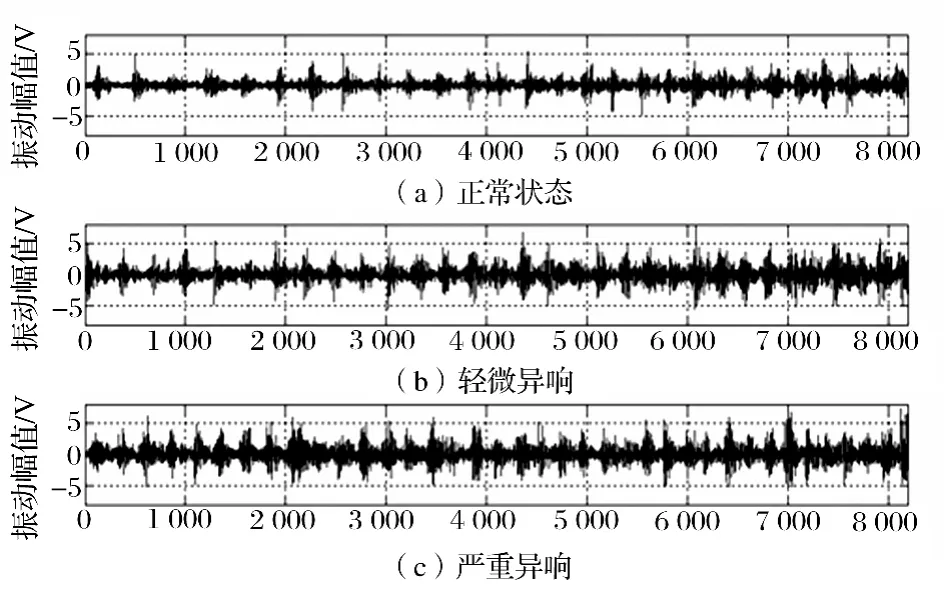
图4 油底与缸体接合处第3缸右侧振动信号

2.2 故障诊断

用小波包滤波产生频带能量进行特征化过程如下。

(1)对信号进行4层小波包分解，提取第4层从低频到高频 16 个频率成分(W［4，i］)的信号特征。

(2)对小波包分解系数重构，提取各频带范围的信号。以 S4，i表示 W［4，i］的重构信号，其中 i=0，1，…，15，则总信号S可以表示为S=

(3)求各频带信号的总能量。输入信号为一随机信号，其输出也为一随机信号。设 S4，i对应的能量为 E4，i，则有∫|Si(t)|2dt。表 1 列出了1 300 r/min测试位置A的小波包AR谱特征能量，可以看出，第2、3、4频段(表格黑体字)的小波包AR谱能量比其他频段能量大，而且随着故障程度渐重，能量对应增强，有效反映了连杆轴承的技术状态变化。

表1 1 300 r/min测试位置A小波包AR谱特征能量

(4)分别选取A、B、C三处加速振动信号进行小波包AR谱分析，计算每个区间的2、3、4频段的功率谱平均能量，作为特征参数构成了模糊聚类分析指标参数，构造特征向量:

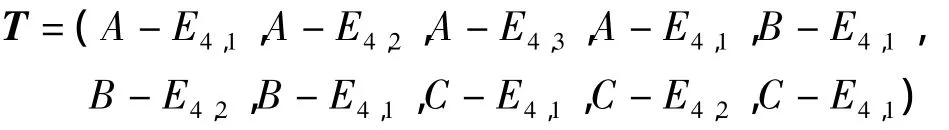
根据以上算法建立的故障样本特征向量见表2。

每类工况随机选择两个样本作为训练集，两个样本作为测试集进行训练和预测。测试结果见表3，6组测试样本的测试结果均与实际状况相一致，诊断正确率为100%。

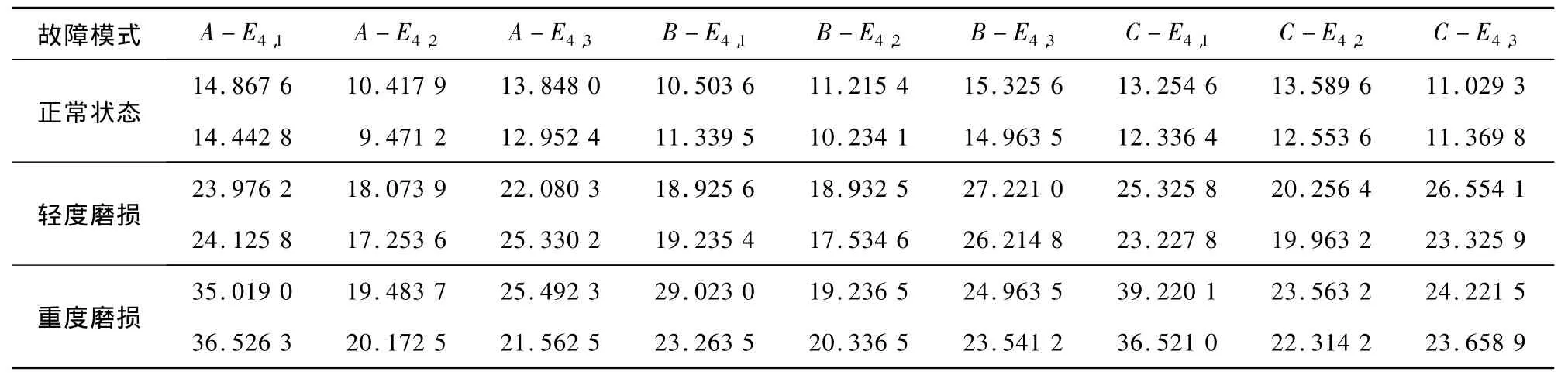
表2 样本特征向量

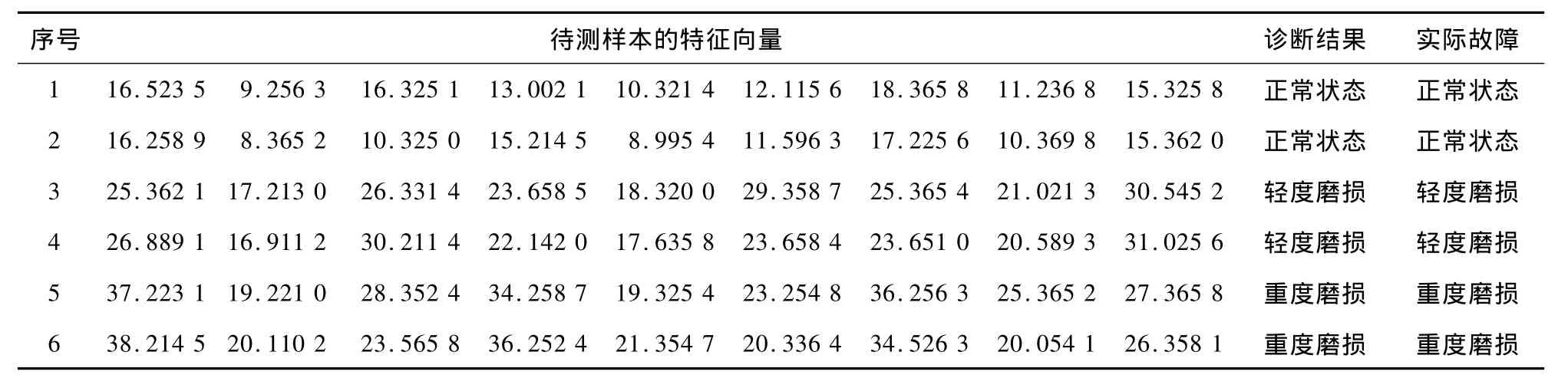
表3 待测样本诊断结果

3 结论

(1)小波包分解，能将包含特征信息的信号与其他干扰信号分解在不同的频带中，实现了特征信息与干扰信息的分离。

(2)对小波包分解的各频带信号进行AR谱分析，能有效提取出包含特征信息的频带，这些频带的信号能量能有效反映连杆轴承的技术状态。

(3)在小样本情况下，SVM模型仍然能够准确识别柴油机各种故障状态，因此通过小波包－AR谱对发动机振动信号进行特征提取，将特征向量输入支持向量机，能有效诊断连杆轴承故障。

［1］ 孔凡让，贾继德，李志远，等.连杆轴承故障诊断研究［J］.中国机械工程，2003，14(6):494-496.

［2］ 贾继德，孔凡让，刘永斌，等.发动机连杆故障噪声诊断研究［J］.农业机械学报，2005，36(6):87-91.

［3］ 张玲玲，任金成，张海峰，等.发动机连杆轴承异响故障分析研究［J］.振动、测试与诊断，2014，34(2):379-384.

［4］ Barell L，Bidini G，Buratti C，et al.Diagnosis of internal combustion engine through vibration and acoustic pressure nonintrusive measurements［J］.Applied Thermal Engineering，2009，29(9):1707-1713.

［5］ 张玲玲，赵懿冠，肖云魁，等.基于小波包－AR谱技术的变速器轴承故障特征提取［J］.振动、测试与诊断，2011，31(4):492-495.

［6］ 刘本得，胡昌华，蔡艳宁.基于聚类和SVM多分类的容差模拟电路故障诊断［J］.系统仿真学报，2009，21(20):6479-6482.

［7］ Saimurugan K I，Ramachandran V S.Multi component fault diagnosis of rotational mechanical system based on decision tree and support vector machine［J］.Expert Systems with Applications，2011，38:3819-3826.

［8］ 杨诚，夏鲁宁，杨振冬.基于小波包和包络谱的齿轮箱异响分析［J］.汽车工程学报，2011，1(5):480-484.

［9］ 胥永刚，孟志鹏，陆明.基于双树复小波包和AR谱的滚动轴承复合故障诊断方法［J］.北京工业大学学报，2014，40(3):335-340

［10］ Vapnik N.An overview of statistical learning theory［J］.IEEE Transactions on Neural Networks，1999，10(5):988-999.

［11］ 肖云魁.汽车故障诊断学［M］.北京:北京理工大学出版社，2006:58-76.