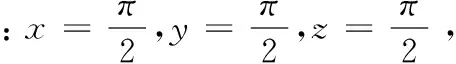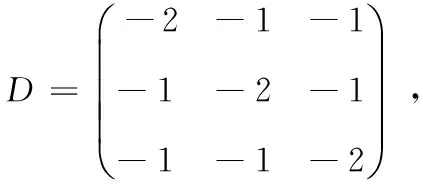多元函数极值的初等变换求解法

孙卫卫

(青岛理工大学琴岛学院, 山东 青岛 266106)

多元函数极值的初等变换求解法

孙卫卫

(青岛理工大学琴岛学院, 山东 青岛 266106)

首先给出了多元函数极值求解的实对称矩阵法，然后受化二次型为标准形的初等变换法的启发，且根据实对称矩阵与二次型之间的关系，得到实对称矩阵的正定性判定的初等变换法.综合以上方法，得到了多元函数极值的初等变换求解法，并给出了相应的定理性的结论.

初等变换；多元函数；极值；实对称矩阵；二次型；标准形；正定性.

1 多元函数极值求解的实对称矩阵法

引入二元函数z=f(x,y)，设它在(x0,y0)的某邻域内连续并且具有一阶与二阶连续的偏导数，并且已知：

fx(x0,y0)=fy(x0,y0)=0，

假设fxx(x0,y0)=A,fxy(x0,y0)=B,fxy(x0,y0)=C，

则有如下结论(一)[1]：

(1)B2-AC<0,在(x0,y0)处取得极值，A>0时取得极小值，A<0时取得极大值；

(2)B2-AC>0,在(x0,y0)处不能取得极值；

(3)AC-B2=0，无法判定.(此结论的证明见参考文献[2][3])

将引入二元函数z=f(x,y)的二阶导数写成矩阵形式即为：

又z=f(x,y)在(x0,y0)的某邻域内连续并且具有一阶与二阶连续的偏导数，故可得：

fxy(x0,y0)=fyx(x0,y0)，

(1)D正定，在(x0,y0)处取得是极小值；(2)D负定，在(x0,y0)处取得是极大值；(3)D不定，在(x0,y0)处不能取得极值.(此结论可由二元函数的泰勒公式进行证明，详见参考文献[2])

将结论(二)推广到三元以及三元以上的函数，得到求三元与三元以上函数极值求解的实对称矩阵法，即定理1[5]：

则有：

(1)D正定，在P0(x10,x20,...,xn0)处取得是极小值；

(2)D负定，在P0(x10,x20,...,xn0)处取得是极大值；

(3)D不定，在P0(x10,x20,...,xn0)处不能取得极值.

2 实对称矩阵的正定性判定的初等变换法

设：

矩阵A对应的二次型为：

(1)

总存在可逆的线性变换X=CY，将其代入(1)中可得标准形：

(2)

例1：求与A合同的对角矩阵：

解：

3 多元函数极值的初等变换求解法

根据定理1、定理2的结论，可得如下定理：

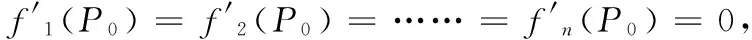
(1)d1，d2，...，dn全都大于零时，在P0(x10,x20,…,xn0)处取得是极小值；

(2)d1，d2，...，dn全都小于零时，在P0(x10,x20,…,xn0)处取得是极大值；

(3)d1，d2，...，dn有正有负时，在P0(x10,x20,…,xn0)处不能取得极值；

(4)其他情况无法判断.

例2：试求三元函数u=f(x,y,z)=sinx+siny+sinz-sin(x+y+z)的极值，其中0

解：先求解方程组

fxx=-sinx+sin(x+y+z)，fxy=sin(x+y+z)，fxz=sin(x+y+z)

fyy=-siny+sin(x+y+z)，fyz=sin(x+y+z)

fzz=-sinz+sin(x+y+z)

由初等变换法可得：

由此可得：

[1] 同济大学数学系.高等数学·下册(第6版)[M].北京:高等教育出版社,2007.

[2] 华东师范大学数学系.数学分析·下册(第4版) [M].北京:高等教育出版社,2010.

[3] 徐森林.数学分析·第3册[M].北京:清华大学出版社 2007.

[4] 吴赣昌.线性代数(第4版)[M].北京：中国人民大学出版社,2011.

[5] 纪跃芝.用矩阵的正定性判定多元函数的极值[J].吉林工学院学报,1995,(4):71-75.

[6] 黄益生.高等代数[M].北京:清华大学出版社,2014.

(责任编校：晴川)

Elementary Transformation Method for the Extreme Value of Multivariate Function

SUN Weiwei

(Qindao College, Qingdao Technological University, Qingdao Shandong 266106, China)

In this paper,the method for solving the extreme value of multivariate function through real symmetric matrix is given. Quadratic form can be simplied into standard form through elementary transformation method. Inspired by this and according to the relationship between the real symmetric matrix and the quadratic form, the elementary transformation method to determine the positive definite of real symmetric matrix is also given. Based on above methods, the elementary transformation method of the extreme value of multivariate function is obtained, and corresponding rational conclusions are given.

elementary transformation; multivariate function; extreme value; real symmetric matrix; quadratic form; standard form;positive definite

2015-07-13

孙卫卫(1982— ),女,山东烟台人,青岛理工大学琴岛学院讲师,硕士.研究方向:应用数学.

O172.1

A

1008-4681(2015)05-0004-02