具有多项差分算子的三阶q-差分方程边值问题
2015-05-04杨小辉李杰民广东警官学院计算机系广东广州5030岭南师范学院数学与计算科学学院广东湛江54048
杨小辉, 李杰民(. 广东警官学院 计算机系, 广东 广州 5030; . 岭南师范学院 数学与计算科学学院, 广东 湛江 54048)
具有多项差分算子的三阶q-差分方程边值问题
杨小辉1, 李杰民2
(1. 广东警官学院 计算机系, 广东 广州 510230; 2. 岭南师范学院 数学与计算科学学院, 广东 湛江 524048)
q-差分方程边值问题解的存在性已经引起国内外数学工作者的研究兴趣,并且得到许多有价值的结果.研究一类三阶q-差分方程边值问题,该问题是由一个三阶q-差分方程和3个具有多项q-差分算子为边界条件构成.这种边界条件可以看成是Sturm-Liouville边界条件的推广.利用Banach压缩映射原理和Krasnoselskii不动点定理,获得了该类边值问题解的存在性和唯一性的充分条件.所得条件简洁,便于验证.结果推广和改进了已有文献中的定理.最后,举2个例子来演示所得结论的应用.
q-差分方程;q-微分;q-积分; 边值问题
1 引言及预备知识
q-差分方程历史悠久[1-4],q-差分方程在多个学科中已得到应用[5-8].近年来q-差分方程解的存在性问题是数学工作者研究的中心问题之一[9-17].Sturm-Liouville型边值问题一直是大家关注的问题[18-21].B. Ahmad等[12]研究了三阶q-差分方程两点边值问题
u(0)=0,Dqu(0)=0,u(1)=0
(1)
C. L. Yu等[15]研究了三阶q-差分方程两点边值问题
u(0)=0,Dqu(0)=0,
(2)
正解的存在性,其中,0
注意到边值问题(1)和(2)仅涉及到一个q-差分算子Dq,而涉及多项q-差分算子的三阶q-差分方程边值问题的研究较少.受到文献[12-13]的启发,本文研究具有4个q-差分算子的三阶q-差分方程两点边值问题
u(0)-αDp1u(0)=0,
u(1)+βDp2u(1)=0,
(3)
其中,0 Δ=1+γ(1+p3)(1+α)+ β(1+p2)+γβ(1+p3)>0. 首先介绍相关概念,然后给出2个引理. 定义 2.1[8]设0 定义 2.2[8]设0 定义 2.3[8]设0 若g在[a,b]上有定义,函数g(t)定义在区间[a,b]上的q-积分定义为 注意到 DqIqg(t)=g(t), IqDqg(t)=g(t)-g(0)(g(t)在t=0处连续). 引理 2.4[8]q-差分算子有如下性质: Dq(gh)(t)=(Dq(g(t))h(t))+g(qt)Dqh(t), 引理 2.5 设y(t)∈C[0,1],则u为边值问题 u(0)-αDp1u(0)=0, u(1)+βDp2u(1)=0, (4) 的解当且仅当 β(1+p2)]y(s)dqs+ (1-p2)dqs}. (5) (6) 对(6)式在[0,t]上进行q-积分得到 (7) 对(7)式在[0,t]上进行q-积分得到 (8) 其中,a0、a1、a2是常数. 当t≠0时, (9) 注意到 又有 (10) 还有 (11) 同理 此时,可知Dpiu(0)=a1. 当t≠0时, 于是有 类似(10)和(11)式可得 (12) 利用(4)式的边值条件 u(0)-αDp1u(0)=0, 可以得到 (13) 把(13)式代入(8)式,并令t=1得到 由(9)式知 所以 (14) 利用u(1)+βDp2u(1)=0得到 (15) (15)式两边通乘以1+q,左边等于 a2[1+γ(1+p3)(1+α)+ β(1+p2)+γβ(1+p3)]=a2Δ, 右边等于 β(1+p2)]y(s)dqs+ 整理得 β(1+p2)]y(s)dqs+ (1-p2)dqs}. (16) 把(16)式代入(13)式,可得a0和a1,把a0、a1和a2代入(8)式得到(5)式,所以u满足(5)式. 反之,设u满足(5)式,容易验证u满足(4)式.证毕. 为了进一步的分析,设X=C[I,R]表示从I到R的所有连续函数集合,定义范数 ‖X‖=sup{|x(t)|,t∈I}. 这时X为Banach空间.记 (1+p2)q](1-p2+β)}. (17) 定理 3.1 设f∈C(I×R,R),I=[0,1],且满足Lipschitz条件 |f(t,u)-f(t,v)|≤L|u-v|, ∀t∈I,u,v∈R, L为Lipschitz常数,则当LH<1时,(3)式有唯一解,其中H为(17)式定义. 证明 构造X上的非线性算子F为 β(1+p2)]f(s,u(s))dqs+ (1-p2)dqs},u∈X. (18) 由f的连续性容易证明F:X→X是全连续算子,u为(18)式的解当且仅当u∈X为F的不动点. 设Br={u∈X:‖u‖≤r},当u∈Br时,有|u(t)|≤r,t∈[0,1],所以 β(1+p2)]f(s,u(s))dqs+ (1-p2)dqs}|≤ f(s,0)|+|f(s,0)|)dqs+ (1+β)(1+q)qs+β(1+p2)]× (|f(s,u(s))-f(s,0)|+|f(s,0)|)dqs+ (|f(s,u(s))-f(s,0)|+|f(s,0)|)dqs]}≤ β(1+p2)dqs+ (1+p2)q](1-p2+β)]}≤ (1+p2)q](1-p2+β)]}≤ (Lr+M)H=LHr+MH≤ LHr+(1-δ)r=(LH+1-δ)r≤r. (H为(17)式所定义.)这表明FBr⊂Br. 设u,v∈X有 [f(s,u(s))-f(s,v(s))]dqs+ β(1+p2)][f(s,u(s))-f(s,v(s))]dqs+ [f(s,u(s))-f(s,v(s))])dqs}|≤ β(1+p2)dqs+ (1+p2)q](1-p2+β)]}=LH‖u-v‖. 当LH<1时,F是压缩映射.由Banach压缩映射原理,F在Br内有唯一不动点u.利用引理2.5,u是(3)式的唯一解. 引理 3.2[18](Krasnoselskii不动点定理) 假设K是Banach空间X的一个非空有界闭凸子集.若算子F1和F2是满足条件: (i)F1x+F2y∈K,x,y∈K; (ii)F1是全连续算子; (iii)F2是压缩算子, 那么存在z∈K使得z=F1z+F2z. 定理 3.3 设f∈C(I×R,R),且满足条件: (A1) |f(t,u)-f(t,v)|≤L|u-v|,L为Lipschitz常数; (A2) 存在φ∈C(I,R+)使得 |f(t,u)|≤φ(t), ∀(t,u)∈I×R, 若Lh<1,其中 (19) 则(3)式至少有一解. 证明 设Banach空间X如第二节定义.算子F1和F2分别如下定义: (F1u)(t)= (1+β)(1+q)qs+β(1+p2)]f(s,u(s))dqs+ (1-p2)dqs},u∈X. 由引理3.2知u为(3)式的解当且仅当u满足u=F1u+F2u.设r≥‖φ‖H且固定,取K={u∈X:‖u‖≤r}.证明分3步完成. 第1步:证当u,v∈K时,F1u+F2v∈K. ‖F2u+F2v‖= β(1+p2)]f(s,v(s))dqs+ (1-p2)dqs}|≤ β(1+p2)]|f(s,v(s))|dqs+ (1-p2+β)|f(s,v(s))|/(1-p2)dqs}|≤ (1+p2)q](1-p2+β)]}≤ (1+p2)q](1-p2+β)]}≤‖φ‖H≤r. 因此F1u+F2v∈K,这表明引理3.2的(i)成立. 第2步:证F1是全连续算子.由条件(A2)知F1是连续,又K有界,于是可设 且t1 ‖(F1u)(t2)-(F1u)(t1)‖= qs(t1-t2)]f(s,u(s))dqs|= 上式表明F1(K)是相对紧的.由Arzelá-Ascoli定理知F1在K上是紧的,所以F1是全连续算子.因此引理3.2的(ii)成立. 第3步:证F2是压缩算子.设u,v∈K时有 ‖F2u-F2v‖= [f(s,u(s))-f(s,v(s))]dqs+ [f(s,u(s))-f(s,v(s))]dqs}|≤ |f(s,u(s))-f(s,v(s))|dqs+ |f(s,u(s))-f(s,v(s))|dqs]}≤ (1+p2)q](1-p2+β)]}≤Lh‖u-v‖. 结合(19)式知F2是压缩算子.因此引理3.2的所有条件都成立.由引理3.2知存在u∈K满足u=F1u+F2u.所以(3)式至少有一解,即定理3.3成立.证毕. 例 4.1 考查如下边值问题 t∈[0,1],L>0, u(1)+D1/4u(1)=0, (20) 则当0 证明 与(3)式对应,易知q=1/2,p1=1/3,p2=1/4,p3=1/5,α=1/4,β=1,γ=1,容易验证Δ=99/20,H≈1.604 5, f=L[t3+cost+1+sinu(t)], 且 |f(t,u)-f(t,v)|= |Lsinu-Lsinv|≤L|u-v|, 当0 例 4.2 考查如下边值问题 t∈[0,1],L>0, u(1)+D1/4u(1)=0, (21) 则当0 证明 与(3)式对应,易知q=1/2,p1=1/3,p2=1/4,p3=1/5,α=1/4,β=1,γ=2,易算得Δ=153/20,h=4 070/3 213, 且 |f(t,u)-f(t,v)|= 当0 注 4.3 文献[12-13]中的定理不能应用到(20)和(21)式. 致谢 刘玉记教授对本文提供了指导,广东警官学院青年项目(2013-Q01)和湛江师范学院自然科学研究项目(QL1101)对本文给予了资助,谨致谢意. [1] Jackson F H. Onq-difference equations[J]. Am J Math,1910,32(4):305-314. [2] Carmichael R D. The general theory of linearq-difference equations[J]. Am J Math,1912,34(2):147-168. [3] Mason T E. On properties of the solutions of linearq-difference equations with entire function coefficients[J]. Am J Math,1915,37(4):439-444. [4] Adams C R. On the linear ordinaryq-difference equation[J]. Ann Math,1928,30(4):195-205. [5] Finkelstein R, Marcus E. Transformation theory of theq-oscillator[J]. J Math Phys,1995,36:2652-2672. [6] Finkelstein R.Theq-Coulomb problem[J]. J Math Phys,1996,37:2628-2636. [7] Gasper G, Rahman M. Basic Hypergeometric Series[M]. Cambridge:Cambridge University Press,1990. [8] Kac V, Cheung P. Quantum Calculus[M]. New York:Springer-Verlag,2002:1-5. [9] Bangerezako G. Variationalq-calculus[J]. J Math Anal Appl,2004,289(2):650-665. [10] Ahmad B, Ntouyas S K. Boundary value problems forq-difference inclusions[J]. Abst Appl Anal,2011,2011:15. [11] Ahmad B, Ahmed A, Ntouyas S K. A study of second-orderq-difference equations with boundary conditions[J]. Adv Diff Eqns,2012,2012:35. [12] Ahmad B. Boundary-value problems for nonlinear third-orderq-difference equations[J]. Electron J Diff Eqns,2011,94:1-7. [13] Wu G C. Variational iteration method forq-difference equations of second order[J]. J Appl Math,2012,2012:1-5. [14] Thiramanus P, Tariboon J. Nonlinear second-orderq-difference equations with three-point boundary conditions[J]. Comput Appl Math,doi:10.1007/s40314-013-0067-x. [15] Yu C L, Wang J F. Eigenvalue of boundary value problem for nonlinear singular third-orderq-difference equations[J]. Adv Diff Eqns,2014,2014:21. [16] Ntouyas S K, Tariboon J. Nonlocal boundary value problems forq-difference equations and inclusions[J]. Inter J Diff Eqns,2015,2015:1-12 [17] Xu N, Zhong C P. Existence and properties of meromorphic solutions of someq-difference equations[J]. Adv Diff Eqns,2015,2015:16. [18] 赵亚明. 奇异Sturm-Liouville型方程与自然边界条件[J]. 四川师范大学学报:自然科学版,1987,15(3):37-42. [19] 罗卫华,吕晓亚,吴开腾. Sturm-Liouville边值问题的正解存在性及其界[J]. 四川师范大学学报:自然科学版,2011,34(1):55-58. [20] 倪黎,韦煜明,茹凯,等. 带p-Laplacian算子Sturm-Liouville型三点边值问题正解的存在性[J]. 广西师范学院学报:自然科学版,2013,30(1):26-28. [21] 王勇,张秋果,韦煜明,等. Sturm-Liouville边值问题三个正解的存在性[J]. 广西师范学院学报:自然科学版,2012,29(2):29-33. [22] 韦煜明,王勇,唐艳秋,等. 具p-Laplacian算子时滞微分方程边值问题解的存在唯一性[J]. 广西师范学院学报:自然科学版,2012,30(2):48-53. [23] 王媛. 二阶差分方程边值问题正解的存在性[J]. 西南大学学报:自然科学版,2009,31(7):58-62. [24] 顿调霞,李永祥. 一类三阶常微分方程的两点边值问题的正解[J]. 四川师范大学学报:自然科学版,2014,37(6):810-813. [25] Smart D R. Fixed Point Theorems[M]. Cambridge:Cambridge University Press,1980. 2010 MSC:39A13 (编辑 李德华) Boundary Value Problem of Third-orderq-Difference Equations with Multi-termq-Difference Operators YANG Xiaohui1, LI Jiemin2 In recent years, an increasing interest in studying the existence of solutions for boundary value problems ofq-difference equations has been observed by the domestic and foreign mathematics workers. And many valuable results have been obtained. In this thesis, a class of third-orderq-difference equations with boundary value conditions is concerned. The boundary value problem is constituted of a third-orderq-difference equation and three boundary conditions containing multi-termq-difference operators. The conditions can be regarded as extension to Sturm-Liouville boundary conditions. By using Banach’s contraction mapping principle and Krasnoselskii’fixed point theorem, sufficient conditions for the existence and uniqueness of solutions of this problem are established. The present conditions are concise and are verified easily. The conclusions in this paper essentially extend and improve known results in references. Finally, two examples are given to demonstrate the use of the main result in this paper. q-difference equation;q-derivative;q-integral; boundary value problem 2014-06-13 公安部应用创新项目(2013YYCXGDST015) 杨小辉(1979—),男,讲师,主要从事微分方程及其应用的研究,E-mail:yxhljq@126.com O175.7 A 1001-8395(2015)06-0875-09 10.3969/j.issn.1001-8395.2015.06.0172 引理
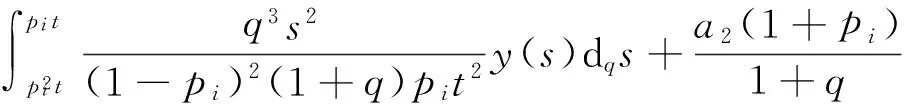
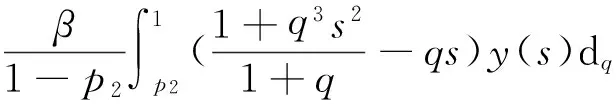

3 主要结论
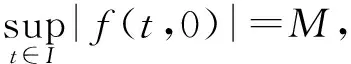
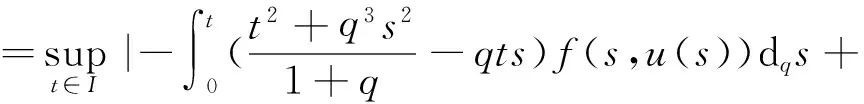

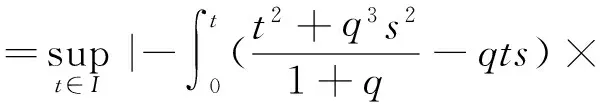

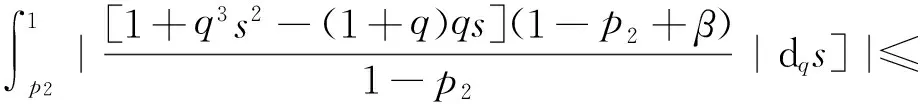
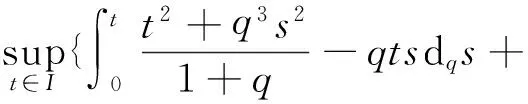
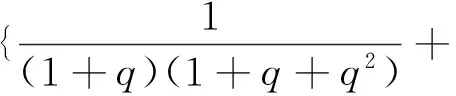


4 例子
(1.DepartmentofComputer,GuangdongPoliceCollege,Guangzhou510230,Guangdong;2.SchoolofMathematicsandComputationalScience,LingnanNormalCollege,Zhanjiang524048,Guangdong)
