偶特征有限域上一类高斯正规基的对偶基及迹基

李雪连, 廖群英(四川师范大学 数学与软件科学学院, 四川 成都 610066)



偶特征有限域上一类高斯正规基的对偶基及迹基

李雪连, 廖群英*
(四川师范大学 数学与软件科学学院, 四川 成都 610066)

设q为2的方幂,文献(李波,廖群英. 数学进展,2015,44(3):394-404.)确定了Fqn在Fq上的一类特殊的高斯正规基及其对偶基的生成元.进一步完全确定了这类正规基的对偶基及迹基的乘法表和复杂度,从而完善了主要结果.并证明了这类正规基的迹基是最优正规基.

有限域; 高斯正规基; 对偶基; 迹正规基; 乘法表; 复杂度

1 引言和主要结果

设q为素数p的方幂,n是正整数,Fqn是有限域Fq的n次扩张(n≥2),若

N={α,αq,…,αqn-1}

为Fqn在Fq上的一组正规基,则称α为Fqn在Fq上的一个正规元.进而令

则T=(ti,j)n×n为N的乘法表,T中非零元素的个数称为N的复杂度,记为CN.由于T=(ti,j)中的非零元越少,Fqn中乘法运算的计算量也就越小,所以寻找低复杂度的正规基是一个很重要的课题.R. Mullin等[1]证明了CN≥(2n-1).且当CN=(2n-1)时,称N为最优正规基,进而给出了两类最优正规基的构造定理,分别为Ⅰ型最优正规基和Ⅱ型最优正规基,并猜想最优正规基只有这2类.随后,S. Gao等[2-3]证明了这个猜想.从而寻找次优的正规基也成了很重要的课题.1990年,A. Wassermann[4]把最优正规基推广到高斯正规基,而这正是一类低复杂度的正规基.

k-型高斯正规基的构造定理[4]设q为素数p的方幂,k和n是正整数,满足kn+1是素数且(kn+1,p)=1.假定δ∈Fqn是kn+1次本原单位根,s是q模kn+1的次数.若(kn/s,n)=1,l是Zkn+1中k次本原单位根,则

生成Fqn在Fq上的正规基N,且其复杂度满足

称N为Fqn在Fq上的k-型高斯正规基.

注 1 当k=1时,1-型高斯正规基即是Ⅰ型最优正规基;当q=k=2时,2-型高斯正规基即是Ⅱ型最优正规基.

2005年,廖群英等[5]给出了有限域Fqn在Fq上Ⅰ型最优正规基和Ⅱ型最优正规基的乘法表;2012年,M. Christopoulou等[6]给出了k=3,4,5,6时,有限域Fqn在Fq上的k-型高斯正规基的乘法表和复杂度的准确公式;廖群英等[7]把文献[6]的结果推广到一般情形,给出了有限域Fqn在Fq上一类k-型高斯正规基的乘法表和复杂度的具体计算公式.

另一方面,在有限域的众多基中,对偶基也是一个很重要的概念.对于Fqn在Fq上的任意2组基:

B={βi=βqi|i=0,1,…,n-1},

N={αi=αqi|i=0,1,…,n-1},

称B为N的对偶基,若对任意的i,j=0,1,…,n-1,都有

其中

是γ∈Fqn在Fq上的迹映射.文献[8]证明了有限域上正规基的存在性,对偶基的存在唯一性以及正规基的对偶基仍为正规基等.2012年,Q. Y. Liao等[9]给出了高斯正规基的对偶基,即证明了如下的结果:

引理 1.1 设q为素数p的方幂,N={α,αq,…,αqn-1}为Fqn在Fq上的k-型高斯正规基(1≤k≤n),则N的对偶基的生成元为

众所周知,在编码理论、密码体制等领域,低复杂度的正规基得到广泛应用[10-12].例如,域F2上元素乘法是实现椭圆曲线公钥密码体制(ECC)的核心运算.由文献[13]可知有限域上的正规基特别是最优正规基更适用于硬件实现,可见寻找低复杂的正规基很重要.设Tr是γ∈F2n在F2上的迹映射,李波等[14]研究了F2n在F2上满足条件

的高斯正规基N={αi=αqi|i=0,1,…,n-1}.证明了:当n=4,8,16时,N满足条件P;但当n=32时,F2n在F2上不存在满足条件P的正规基,并进一步给出偶特征有限域上满足条件P的正规基的存在性条件,即证明了如下的结果.

引理 1.2[14]设n≥k>1,q为2的方幂,N为Fqn在Fq上的k-型高斯正规基,则

1) 当k≡0(mod 2)时,N不满足条件P.

2) 当k≡1(mod 2)时,N满足条件P当且仅当n=4且k=1或者k=3.

本文进一步研究偶特征有限域上满足条件P的高斯正规基,给出了其对偶基与迹基的乘法表和复杂度等,即证明了如下主要结果.

定理 1.3 设n≥k>1,q为2的方幂,N为Fqn在Fq上满足条件P的k-型高斯正规基,B为N的对偶基,CB为B的复杂度,则B满足条件P,且

定理 1.4 设q为2的方幂,N为Fqn在Fq上满足条件P的k-型高斯正规基,M为N的迹正规基,则M是Fq2在Fq上的最优正规基.

2 主要结果的证明

为证明定理1.3和1.4,需要如下几个引理.

引理 2.1[15]设q为素数p的方幂,

N={α,αq,…,αqn-1}

是Fqn在Fq上的k-型高斯正规基,

是α∈Fqn在Fq上的迹映射,则Tr(α)=-1.

引理 2.3[16]设q为素数p的方幂,n是正整数,Fqn是有限域Fq的n次扩张(n≥2).若正整数m为n的因数,且N={α,αq,…,αqn-1}为Fqn在Fq上的正规基,则

生成Fqm在Fq上的正规基M={γ,γq,…,γqm-1},称为N的迹正规基.

定理1.3的证明 设N={αi=αqi|i=0,1,2,3}是Fq4在Fq上满足条件P的k-高斯正规基,则由引理1.2可知q为2的方幂且k=1或3.设

B={βi=βqi|i=0,1,2,3}

为N的对偶基,注意到q为2的方幂且k=1或3,故由引理1.1可得

于是相应地有

β1=βq=1+α3,

β2=β1q=1+α0,

β3=β2q=1+α1.

(1)

从而由αi=αqi(i=0,1,2,3)可得

ββ0=(1+α2)2=

1+α2α2=1+(αα0)q2,

(2)

ββ1=(1+α2)(1+α3)=

1+α2+α3+α2α3,

(3)

ββ2=(1+α2)(1+α)=

1+α2+α+α2α,

(4)

ββ3=(1+α2)(1+α1)=

1+α2+α1+α1α2.

(5)

情形一 当k=1时,N是Ⅰ型最优正规基,于是由文献[5]的定理1可知N的乘法表T=(tij)4×4满足:当j=0,1,2,3时,有t2,j=-1;当i=0,1,3时,

又由k=1,n=4以及k-型高斯正规基的构造定理可知,q模5的阶为4,从而

或

进而由q是2的方幂,可知N的乘法表T=(tij)4×4形如

(6)

或

(7)

1) 若N的乘法表为(6)式,则

αα0=α1,αα1=α3,

αα2=α+α1+α2+α3,αα3=α2.

(8)

又由引理2.1知1=Tr(α)=α+α1+α2+α3,其中Tr是Fq4到Fq上的迹映射.从而由(2)～(5)式及(8)式可得

ββ0=1+(αα0)q2=

1+(α1)q2=1+α3=β1,

(9)

ββ1=1+α2+α3+α2α3=

1+α2+α3+α1=β+β1+β3,

(10)

ββ2=1+α2+α+α2α=

1+α1+α3=α+α2=β+β2,

(11)

以及

ββ3=1+α2+α1+α0=β+β2+β3.

(12)

故此时B的乘法表为

且CB=9.进而由引理2.1,以及(1)、(9)～(12)式可知

即B也满足条件P.

2) 若N的乘法表为(7)式,则

αα0=α3,αα1=α2,

αα2=α+α1+α2+α3,αα3=α1.

(13)

于是由(2)～(5)以及(13)式得到:

ββ0=1+(α3)q2=1+α1=β3,

(14)

ββ1=1+α2+α3+α2α3=

1+α2+α3+α0=β+β1+β2,

(15)

ββ2=1+α2+α+α2α=

1+α2+α+α+α1+α2+α3=

β+β2,

(16)

ββ3=1+α2+α1+α3=β+β1+β3.

(17)

从而相应的B的乘法表为

即CB=9.进而由引理2.1,以及(1)、(14)～(17)式有

因此B也满足条件P.综上可知,CB=9且B也满足条件P,即定理1.3的第一种情形成立.

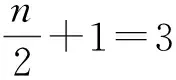
(18)

同理

(19)

和

(20)

以及

(21)

于是由(1)～(5)式可知,相应地

(22)

(23)

(24)

注 2 由正规基的概念可知ββ2=0的情形是不存在的,所以ββ2只可能有以下5种情形

ββ2=1+α2+α+α2α=

(25)

以及

ββ3=1+α2+α1+α1α2=

(26)

于是由正规基的乘法表及复杂度的定义可知,B的复杂度CB满足

7=2n-1≤CB≤1+3+4+3=11.

又由引理2.1,以及(22)～(23)、(25)～(26)式可得

故此时B也满足条件P.这就证明了定理1.3的第二种情形.

定理1.4的证明 由N满足条件P,及引理1.2知q为2的方幂且n=4,k=1或k=3.于是由引理2.3可知N的迹正规基M={γ,γq},其中Tr是Fq4到Fq2上的迹映射,且

γ=Tr(α)=α+αq2=α+α2∈Fq2/Fq, (27)

γq=Tr(αq)=αq+αq3=α1+α3∈Fq2/Fq. (28)

情形一 当n=4且k=1时,由定理1.3第一种情形的证明,可知有如下2种情形.

1) 当N的乘法表为(6)式时,即

αα0=α1,αα1=α3,

αα2=α+α1+α2+α3=1,αα3=α2，

故

γγ=(α+αq2)(α+αq2)=αα+α2α2=

αα+(αα)q2=α1+(α1)q2=α1+α3=γq,

γγq=(α+αq2)(α+αq3)=

αα1+αα3+α1α2+α2α3=

α3+α2+(αα1)q+(αα1)q2=

α3+α2+(α3)q+(α3)q2=

α3+α2+α+α1=γ+γq.

因此M的乘法表

故CM=3.

2) 当N的乘法表为(7)式时,类似可得

故CM=3=2×2-1.

综上可知,当n=4,且k=1时,N的迹正规基M是Fq2在Fq上的最优正规基.

情形二 当n=4,k=3时,由(27)～(28)式可知:

γγ=(α+αq2)(α+αq2)=

αα+α2α2=αα+(αα)q2,

γγq=(α+α2)(α1+α3)=

αα1+αα3+α1α2+α2α3=

αα1+αα3+(αα1)q+(αα1)q2.

故γγ,γγq的取值决定于αα,αα1,αα3.而由(18)～(21)式知αα有3种取法,αα1有4种取法,αα3有4种取法,且αα1≠αα3.故有以下22种情形.

情形1:当αα=α1,αα1=α+α1+α2,αα3=α+α1+α3时,

γγ=αα+(αα)q2=α1+α3=γq,

γγq=αα1+αα3+(αα1)q+(αα1)q2=

α+α2+α1+α3=γ+γq.

于是

故CM=3.

情形2:当αα=α1,αα1=α+α1+α2,αα3=α1+α2+α3时.

情形3:当αα=α1,αα1=α+α2+α3,αα3=α1+α2+α3时.

情形4:当αα=α1,αα1=α+α1+α3,αα3=α+α2+α3时.

情形5:当αα=α1,αα1=α1+α2+α3,αα3=α+α1+α2时.

情形6:当αα=α3,αα1=α+α1+α2,αα3=α+α1+α3时.

情形7:当αα=α3,αα1=α+α1+α2,αα3=α1+α2+α3时.

情形8:当αα=α3,αα1=α+α2+α3,αα3=α1+α2+α3时.

情形9:当αα=α3,αα1=α+α1+α3,αα3=α+α2+α3时.类似都可以得到

故CM=3.

情形10:当αα=α1,αα1=α+α1+α2,αα3=α+α2+α3时,

γγ=αα+(αα)q2=α1+α3=γq,

γγq=αα1+αα3+(αα1)q+(αα1)q2=

α+α1+α2+α+α2+α3+

α1+α2+α3+α+α2+α3=

α+α3.

又由引理2.1知:α+α2+α1+α3=-1,即γ+γq=-1=1,q≡0(mod2).注意到:(α+α3)q2=α1+α2且α+α3=γγq∈Fq2,于是(α+α3)q2=α+α3,故α1+α2=α+α3,从而α1+α2+α+α3=0,与引理2.1矛盾,故此情形不成立.

情形11:当αα=α1,αα1=α+α2+α3,αα3=α+α1+α3时.

情形12:当αα=α1,αα1=α+α2+α3,αα3=α+α1+α2时.

情形13:当αα=α1,αα1=α+α1+α3,αα3=α+α1+α2时.

情形14:当αα=α1,αα1=α+α1+α3,αα3=α1+α2+α3时.

情形15:当αα=α1,αα1=α1+α2+α3,αα3=α+α2+α3时.

情形16:当αα=α1,αα1=α1+α2+α3,αα3=α+α1+α3时.

情形17:当αα=α3,αα1=α+α1+α2,αα3=α+α2+α3时.

情形18:当αα=α3,αα1=α+α2+α3,αα3=α+α1+α3时.

情形19:当αα=α3,αα1=α+α2+α3,αα3=α+α1+α2时.

情形20:当αα=α3,αα1=α+α1+α3,αα3=α+α1+α2时.

情形21:当αα=α3,αα1=α+α1+α3,αα3=α1+α2+α3时.

类似可得到这些情形都有:α1+α2+α+α3=0,与引理2.1矛盾.

情形22:即αα=α2时,γγ=αα+(αα)q2=α+α2=γ,从而γ=1或0,这与γ生成迹正规基N相矛盾.

综上所述M的乘法表为

且CM=3,故M是Fq2在Fq上的最优正规基.这就证明了定理1.4.

3 举例

本节考虑q=2和q=8时,Fq4在Fq上满足条件P的3-型高斯正规基的对偶基及迹基的乘法表和复杂度.

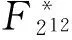
生成F24在F2上的3-型高斯正规基N,并且

α1=α2=(δ+δ3+δ9)2=

δ2+δ6+δ18=δ2+δ6+δ5,

α2=α12=(δ2+δ6+δ5)2=δ4+δ12+δ10,

α3=α22=(δ4+δ12+δ10)2=

δ8+δ20+δ24=δ8+δ7+δ11.

从而

αα0=α2=α1,

αα1=(δ+δ3+δ9)(δ2+δ6+δ5)=α+α1+α3,

αα2=(δ+δ3+δ9)(δ4+δ10+δ12)=α+α2,

αα3=(δ+δ3+δ9)(δ7+δ8+δ9)=α+α2+α3.

故由α生成的F24在F2上的3-型高斯正规基N的乘法表为

从而N的复杂度CN=9.进而设N的对偶基

B={βi=β2i|0≤i≤3},

则由引理1.1以及(1)～(5)式可知

ββ0=1+α22=1+α3=β1,

ββ1=1+α2+α3+α2α3=β1+β2+β3,

ββ2=1+α2+α+α2α=β+β1+β2+β3,

ββ3=1+α2+α1+α2α1=β3.

即B的乘法表为

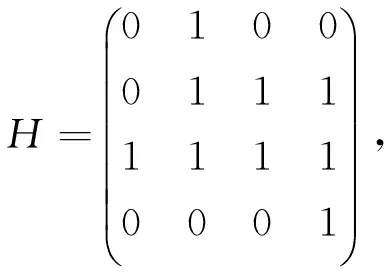
从而B的复杂度CB=9.又设N的迹正规基M={γ,γ2},则由引理2.3知

γ=Tr(α)=α+α22=α+α2,

γ2=Tr(α2)=α2+α23=α1+α3.

故

γγ=αα+(αα)22=α1+α3=γ2,

γγ2=αα1+αα3+(αα1)2+(αα1)22=

α+α2+α1+α3=γ+γ2.

于是

且CM=3.

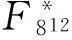
生成F84在F8上的3-型高斯正规基N,并且

α1=α8=(δ+δ3+δ9)8=

δ8+δ24+δ72=δ8+δ11+δ7,

α2=α18=(δ8+δ11+δ7)8=

δ64+δ88+δ56=δ12+δ10+δ4,

α3=α28=(δ12+δ10+δ4)8=

δ96+δ80+δ32=δ5+δ2+δ6.

从而

αα0=(δ+δ3+δ9)2=δ2+δ6+δ5=α3,

αα1=(δ+δ3+δ9)(δ7+δ8+δ11)=α+α1+α2,

αα2=(δ+δ3+δ9)(δ4+δ10+δ12)=α+α2,

αα3=(δ+δ3+δ9)(δ5+δ2+δ6)=α+α1+α3.

故由α生成的F84在F8上的3-型高斯正规基N的乘法表为

且N的复杂度CN=9.进而设N的对偶基

B={βi=β8i|0≤i≤3},

则由引理1.1以及(1)～(5)式可知:

ββ0=1+α22=1+α1=β3,

ββ1=1+α2+α3+α2α3=β2,

ββ2=1+α2+α+α2α=β+β1+β2+β3,

ββ3=1+α2+α1+α2α1=β1.

从而B的乘法表为

且B的复杂度CB=7.可见此对偶基B是F84在F8上的最优正规基.又设N的迹正规基M={γ,γ8},则由引理2.3知

γ=Tr(α)=α+α82=α+α2,

γ8=Tr(α8)=α8+α83=α1+α3.

故

γγ=αα+(αα)82=α1+α3=γ8,

γγ8=αα1+αα3+(αα1)8+(αα1)82=

α+α2+α1+α3=γ+γ8.

于是

且CM=3.

致谢 四川师范大学科研重点培育项目 (13ZDL06)对本文给予了资助,谨致谢意.

[1] Mullin R, Onyszchuk I, Vanstone S, et al. Optimal bases inGF(pm)[J]. Discrete Applied Math,1988/1989,22(2):149-161.

[2] Gao S, Lenstra H Jr. Optimal normal bases[J]. Design,Codes and Cryptography,1992,2:315-323.

[3] Gao S. Normal Bases over Finite Fields[D]. Ontario:Waterloo,1993.

[4] Wassermann A. Konstruktion von normal basen[J]. Bayreuther Mathematische Schriften,1990,31:155-164.

[5] 廖群英,孙琦. 有限域上最优正规基的乘法表[J]. 数学学报,2005,48(5):947-954．

[6] Christopoulou M, Garefalakis T, Panario D, et al. Gauss periods as constructions of low complexity normal bases[J]. Designs,Codes Cryptography,2012,62(1):43-62.

[7] 廖群英,胡晓兰. 有限域上一类高斯正规基的复杂度的准确计算公式[J]. 数学学报,2014,57(5):863-874.

[8] Menezes A J, Blake I F, Gao X H, et al. Applications of Finite Fields[M]. New York:Kluwer Academic Publishers,1993.

[9] Liao Q Y. The gaussian normal basis and its trace basis over finite fields[J]. J Numb Theory,2012,132(7):1507-1518.

[10] Beth T. Generalizing the discrete fourier transform[J]. Discrete Math,1985,56:95-100.

[11] Diffie W, Hellman M. New directions in cryptography[J]. IEEE Trans Inform Theory,1976,22:644-654.

[12] Fumy W. orthogonal transform encoding of cyclic codes[C]//Algebraic Algorithms and Error-Correcting Codes. Lecture Notes Comput Sci. Berlin:Spring-Verlag,1986,229:131-134.

[13] Dahab R, Hankerson D. Software multiplication using gaussian normal basis[J]. IEEE Transaction on Computers,2006,55(8):974-984.

[14] 李波,廖群英. 偶特征有限域上一类正规基及其对偶基[J]. 数学进展,2015,44(3):394-404.

[15] 李俊,黄琴,李波,等. 有限域上k-型高斯正规基及其对偶基[J]. 四川师范大学学报:自然科学版,2011,34(3):289-295.

[16] Christopoulou M, Garefalakis T, Panario D, et al. The trace of an optimal normal element and low complexity normal bases[J]. Designs,Codes Cryptography,2008,49(1/2/3):199-215.

2010 MSC：12E20

(编辑 陶志宁)

The Trace and Dual Bases of Some Special Gaussian Normal Bases over Finite Fields with Even Characteristic

LI Xuelian, LIAO Qunying
(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Letqbe a power of 2. Recently, the dual basis of some special Gaussian normal base of the finite filedFqnoverFqis determined in literature(Li B, Liao Q Y. Adv Math(China),2015,44(3):394-404.). The present paper continues the study and determines the complexity of the dual and trace basis for the above Gaussian normal bases completely, and it is proved that the trace basis is optimal.

finite field; Gauss normal basis; dual basis; trace normal basis; multiplication table; complexity

2014-08-22

国家自然科学基金(11401408)和四川省教育厅重点项目基金(14ZA0034)

O156.2; O157.4

A

1001-8395(2015)06-0802-08

10.3969/j.issn.1001-8395.2015.06.003

*通信作者简介：廖群英(1974—),女,教授,主要从事编码与密码学理论的研究,E-mail:qunyingliao@sicnu.edu.cn.