关于有限域上特殊本原元的存在性
2015-05-04廖群英四川师范大学数学与软件科学学院四川成都610066
廖 欢, 廖群英(四川师范大学 数学与软件科学学院, 四川 成都 610066)
关于有限域上特殊本原元的存在性
廖 欢, 廖群英*
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
设Fq为有限域,文献(P. P. Wang, et al. Finite Fields and Their Applications,2012,18(4):800-813.)给出了特征为2的有限域Fq中存在α∈Fq使得α和α+α-1都是Fq中本原元的几个充分条件,随后,文献(Q. Y. Liao, et al. Chin Annals Math,2015, in press.)将其结果推广到任意特征的有限域上.讨论任意特征的有限域Fq中存在2个本原元α,β,使得α+β亦为本原元的几个充分条件,进而,利用特征和的方法得到一个满足此条件的q的下界q0=4.98×1086.最后,利用计算机验证了特征为2的有限域除F2与F4外均满足此条件.
有限域; 本原元; 乘法特征; 特征和
有限域作为一种特殊的域,在编码理论、组合设计、密码学等许多实际领域都有着非常广泛的应用[1-4].特别是20世纪中期以来,随着计算机技术的发展,有限域的地位愈加重要,许多从事应用研究的数学家开始有限域的理论研究,有限域理论已经成为许多工程技术人员不可缺少的数学工具.另一方面,有限域理论本身也引起人们的广泛兴趣,其中许多问题推动着数学的发展[5].
设q是素数方幂,Fq是q元有限域.熟知,Fq*=Fq{0}为循环群,其生成元称为有限域Fq的本原元.有限域上的本原元在有限域的代数结构中起着至关重要的作用,而且由于有限域理论在各个专业领域中的广泛应用,有限域上的本原元已经成为一个热点问题.1984年,S. W. Golomb[6]在研究Costas阵列的设计问题时,提出如下猜想:存在正整数q0,使得当素数方幂q>q0时,有限域Fq的任一非零元皆可表为其2个本原元的和.
对于此猜想,孙琦[7]给出了一个下界q0=260,常彦勋亦给出了当q>6.62×107,且q≠3.006 903 91×108时,Fq的任一非零元皆可表为其2个本原元的和[8],基本解决了此猜想.此外,文献[9-10]研究了更一般的问题:存在正整数q0,当q>q0时,对任意a,b,α∈Fq,均存在Fq的2个本原元x和y使得ax+by=α并得到了与Golomb猜想类似的结果.贺龙斌等[11]解决了形如α+α-1的本原元存在的条件,P. P. Wang等[12]进一步研究了特征为2的有限域Fq中使得α和α+α-1都是Fq中本原元的元素α的存在性条件,随后,Q. Y. Liao等[13]将其结果推广到了一般的有限域.
本文在此基础上进一步讨论在什么条件下,有限域Fq中存在2个本原元α和β,使得α+β亦为Fq中的本原元,即寻找素数方幂q属于集合
U={q|存在Fq中元素α,β使得α,β,
α+β均为Fq中的本原元}
的一些充分条件.
本文用特征和估计的方法得到如下主要结果.
定理 1 设Fq为q元有限域,若q满足q>24ω(2ω-1)2,其中ω=ω(q-1)为q-1的不同素因子个数,则q∈U.
推论 2 设Fq为q元有限域,若ω(q-1)≥49,则q∈U.
推论 3 设Fq为q元有限域,若q>4.98×1086,则q∈U.
1 预备知识
关于有限域的基本性质可参见文献[5].本节主要介绍有限域的乘法特征的相关性质,其他详细性质可见文献[14].
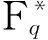
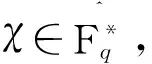
根据引理4,易知对任意η∈Fq,均有
从而有如下结果.
).
下面关于乘法特征和的估计是本文证明主要结果的关键.
引理 6[15]设fi(T)(i=1,2,…,n)是Fq[T]中两两互素的无平方因子的首1多项式,degfi=di(1≤i≤n).若χ1,χ2,…,χn为Fq的非平凡的乘法特征,则有
设ξ∈Fq,d为正整数.定义
这里μ为莫比乌斯函数,ord(χ)表示乘法特征χ的阶.则有如下结论.
引理 7[16]设ξ∈Fq,d|q-1.P(ξ)的定义如上所示,则有

2 主要结果的证明
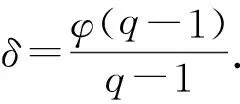
N1+N2+…+N8,
(1)
其中
P(b,β)P(c,α+β).
下面分别计算Ni(1≤i≤8),易知
(2)
对于N2有

N2=0.
(3)
对于N3有
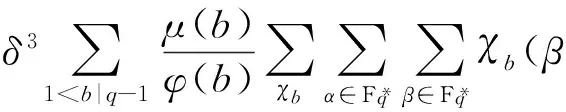
N3=0.
(4)
对于N4,类似于N3的计算,同理可知
N4=0.
(5)
对于N5有
(6)
对于N6有

(7)
对于N7,与N6的计算类似的有
(8)
最后,对于N8有
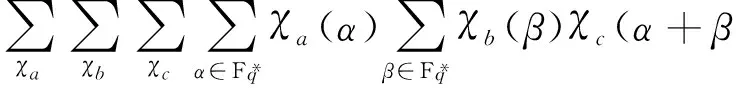
(9)
由(1)~(9)式可知
|N(q)-N1|≤|N6|+|N7|+|N8|.
因此,欲使N(q)>0,只需N1>|N6|+|N7|+|N8|,即
(10)
易知,(10)式成立的一个充分条件为
此式等价于
(11)
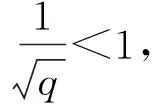
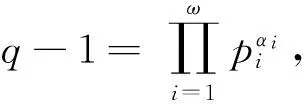
又由定理1可知,若
则q∈U.
通过计算可知,当ω<49时,I(ω)<0,且I(49)>0.
以下证明:对任意n≥49,均有I(n)>0.对n作归纳证明.
当n=49时,结论成立.
现设n≥49且I(n)>0,则有
Pn24n(2n-1)2-24(n+1)(2n+1-1)2=
Pn24n(2n-1)2-16·24n(2·2n-1)2.
由于n≥49,所以Pn>144,从而
I(n+1)>144·24n(2n-1)2-
16·24n(2·2n-1)2=
16·24n·[9(2n-1)2-(2·2n-1)2].
又由3(2n-1)≥2·2n-1,可知I(n+1)>0.
这就证明了推论2.
推论3的证明.由定理1及推论2可知:若q∉U,则ω(q-1)<49且q≤24ω(2ω-1)2.容易看到24ω(2ω-1)2是关于ω的增函数,所以当q>24·48(248-1)2时,q∈U.而24·48(248-1)2≈4.97×1086,故当q>4.98×1086时,q∈U.
3 特征为2的情形
推论3给出了q满足条件q∈U的一个下界q0=4.98×1086,对所有的q=2s≤q0,用数学软件maple进行逐一筛选与计算,得到如下结论.
定理 8 除去F2、F4外,所有特征为2的有限域Fq(q=2s)均满足q∈U.
证明 对于F2,其单位元1是唯一的本原元.而对于F4={0,1,θ,1+θ},其中θ为F2上不可约多项式T2+T+1的根,其全部本原元为θ,1+θ.所以2,4均不属于U.
以下考虑F2s,其中s≥3.由于q0=4.98×1086,故[log2q0]=288,其中[·]为高斯取整函数.因此3≤s≤288.此时由定理1及推论2知,要确定集合
S={s|s<288,ω(2s-1)<49,
q>24ω(2s-1)(2ω(2s-1)-1)2}.
由如下的程序1计算可知
S={2,3,4,6,8,9,10,11,12,14,15,16,
18,20,22,24,28,30,36,40,48,60}.
其次,对所有s∈S,利用如下的程序2来实际查找F2s中满足条件的本原元α和β.经计算与验证可知定理8成立.
程序 1
restart
with(numtheory)
w:=x->nops(factorset(x))
w0:=48
i:=1
q:=2i
exception:=NULL
while q if w(q-1)<49 and q-24*w(q-1)(2w(q-1)-1)2<=0 then exception:=exception,i end if i:=i+1 q:=2i end do print(exception) 程序 2 Lastexception:=NULL for s in exception do G:=GF(2,s) PE:=G:-PrimitiveElement() N:=0 for i from 1 to 2s-2 do for j from i+1 to 2s-1 do if igcd(i,2s-1)=1 and igcd(j,2s-1)=1 then PEI:=G:-`'(PE,i) PEJ:=G:-`'(PE,j) SUM:=G:-`+`(PEI,PEJ) if G:-isPrimitiveElement(SUM)=true then N:=1 break end if end if end do if N=1 then break end if end do if N=0 then Lastexception:=Lastexception,s end if end do print(Lastexception) 实际上,对每一个s∈S,均利用程序2具体的给出相应的F2s中满足α+β为本原元的2个本原元α和β.但由于当s较大时,其表达式较为繁复,在此仅给出其中2例. 例 2 对于s=8的情形,即F28=F2(θ),其中θ为不可约多项式T8+T7+T5+T3+1的根.取两本原元α=T7+T5+T4+T3+T2,β=T6+T4+T3+1.则容易验证α+β=T7+T6+T5+T2+1亦为本原元,所以28∈U. [1] 冯克勤. 纠错码的代数理论[M]. 北京:清华大学出版社,2005. [2] 周玉洁,冯登国. 公开密钥密码算法及其快速实现[M]. 北京:国防工业出版社,2002. [3] 李欣妍,芦殿军. 基于椭圆曲线密码体制的代理多重盲签名[J]. 计算机工程与科学,2010,32(11):58-59. [4] 陈家琪,冯俊,郝妍. 无证书密钥协商协议对跨域Kerberos的改进[J]. 计算机工程,2010,36(20):150-152. [5] 林东岱. 代数学基础与有限域[M]. 北京:高等教育出版社,2006. [6] Golomb S W. Algebraic constructions for Costas arrays[J]. J Combinatorial Theory,1984,A37(1):13-21. [7] 孙琦. 关于有限域中的元根[J]. 四川大学学报:自然科学版,1988,25(2):133-139. [8] 常彦勋,康庆德. 有限域中非零元表为两本原元和的问题[J]. 中国科学,1990,A11:1146-1153. [9] 常彦勋. 有限域的本原元性质[J]. 数学杂志,1993,13(1):59-63. [10] 王巨平. Golomb猜想[J]. 中国科学,1987,A9:927-935. [11] 贺龙斌,韩文报. 有限域上形如α+α-1的本原元的研究[J]. 信息工程大学学报,2003,4(2):97-98. [12] Wang P P, Cao X W, Feng R Q. On the existence of some specific elements in finite fields of characteristic 2[J]. Finite Fields and Their Applications,2012,18(4):800-813. [13] Liao Q Y, Li J Y, Pu K L. On the existence for some special primitive elements in finite fields[J]. Chinese Annals of Mathematics,2015, in press. [14] 冯克勤,廖群英. 有限域及其应用[M]. 大连:大连理工大学出版社,2011. [15] Wan D Q. Generators and irreducible polynomials over finite fields[J]. Mathematics of Computation of the American Mathematical Society,1997,66(219):1195-1212. [16] Cohen S D. Primitive roots in the quadratic extension of a finite field[J]. J London Mathematical Society,1983,2(2):221-228. 2010 MSC:11T30 (编辑 郑月蓉) On the Existence for Specific Primitive Elements over Finite Fields LIAO Huan, LIAO Qunying Let Fqbe theqelements finite field. The literature(P. P. Wang, et al. Finite Fields and Their Applications,2012,18(4):800-813.) obtains several sufficient conditions for the existence ofα∈ Fqsuch thatαandα+α-1are both primitive elements in Fq. Recently, the work(Q. Y. Liao, et al. Chin Annals Math,2015, in press.) generalizes their main results to the finite field with arbitrary characteristics. In this paper, we obtain a sufficient condition for the existence of the finite field Fqin which there exist two primitive elementsα,β∈ Fq, such that α+β is also a primitive element of Fq. Furthermore, for finite fields satisfying this condition, by using character sums, we get a lower bound of the correspondingq. Finally, we verify that the condition is true for all finite fields with characteristic 2 except F2and F4. finite field; primitive element; multiplicative character; character sum 2013-12-19 国家自然科学基金(11401408)和四川省教育厅重点项目 (14ZA0034) O153.4 A 1001-8395(2015)06-0797-05 10.3969/j.issn.1001-8395.2015.06.002 *通信作者简介:廖群英(1974—),女,教授,主要从事数论与编码的研究,E-mail:qunyingliao@sicnu.edu.cn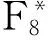
(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)
