面向图像分类的多层感知机BBO优化方法
2015-05-04朱黎辉李晓宁四川师范大学计算机科学学院四川成都610101
朱黎辉, 李晓宁(四川师范大学 计算机科学学院, 四川 成都 610101)
面向图像分类的多层感知机BBO优化方法
朱黎辉, 李晓宁*
(四川师范大学 计算机科学学院, 四川 成都 610101)
为了通过优化多层感知机权重及偏置提高图像分类决策的正确率,借鉴生物地理学优化(BBO)算法的思想,提出面向图像分类的多层感知机BBO方法.首先提取图像的颜色矩和降维梯度方向直方图(DRHOG)的组合特征作为多层感知机的输入数据,然后使用BBO优化方法得到迭代250次的最优权重及偏置,最后经多层感知机得出测试图像的类别.该方法有效避免算法早熟现象,增强图像分类能力.通过仿真实验,验证此方法比粒子群优化算法优化多层感知机具有更高的求解质量和效率,为图像分类提供又一可行方案.
生物地理学优化; 多层感知机; 颜色矩; 降维梯度方向直方图; 粒子群优化
随着网络技术的普及,图像数量呈指数级增长趋势,在大数据集的图像数据库中查找符合条件的图片成为了当前网络技术研究热点.图像分类作为其中的一项重要技术,已成为重点研究方向.图像分类研究集中在图像特征提取和分类器的选择上.图像特征主要有3类,一是基于颜色特征的颜色矩和颜色直方图等;二是基于形状特征的梯度方向直方图[1]、zernike矩[2]等;三是基于纹理特征的灰度共生矩阵[3]、局部二值模式[4]等.分类器主要包括支持向量机、神经网络、在线分类器[5]等.另外,特征的优化问题得到广泛关注.本文结合实际项目,主要研究图像分类中的优化问题.
常用于优化问题的启发式算法有粒子群优化(PSO)[6]、遗传算法(GA)[7]等,生物地理学优化(BBO)[8]算法是近几年才提出的启发式算法,它是受动物或其他物种的迁移策略启发来求解优化问题的算法,文献[9]已证明BBO算法具有较佳的优化能力,因此被应用到实际生活中的优化问题,包括车间调度问题[10]、移动机器人控制系统[11]、电力系统优化[12]等.著名的没有免费午餐定理(NFL)证明没有一个启发式算法适合解决所有优化问题[13],PSO较GA,具有将能获得较优解的所有粒子记忆下来,而GA随着种群的改变会破坏之前的较优解,PSO以更快速度收敛于最优解的概率更大;BBO不仅能保留每次迭代最佳解,而且其拥有变异算子能增强搜索能力;GA作为进化算法也具有突变算子,但是通常在整个种群中只有一个突变算子,而BBO增加了更多的可变性,每个种群拥有不同的突变常量.从理论出发,综合考量后,本文采用BBO优化算法进行特征优化,并用对比实验验证,BBO优化算法具有较强的鲁棒性.
多层感知机(MLP)属于前向神经网络(FNN)[14],它是神经网络中最著名和使用最广泛的形式[15].因此本文提出基于BBO优化算法的MLP图像分类方法.MLP输入数据为颜色矩和DRHOG的组合特征,DRHOG特征是基于传统梯度直方图的改进特征,本文方法提供了一种较少特征向量来高效解决图像分类的方法.
1 多层感知模型
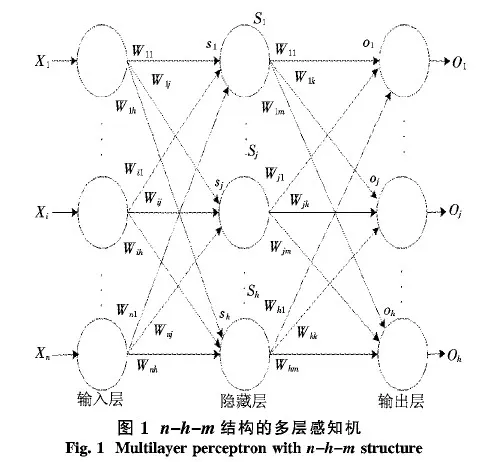
图1为一个结构为n-h-m的3层感知机,包括输入层、隐藏层、输出层.输入节点个数是n,隐藏节点个数为h,输出节点个数为m,节点之间存在单向连接.MLP的输出的计算流程如图1所示.
1) 计算输入的加权和.具体计算为(1)式,其中,n是输入节点的数目,Wij是从输入层第i节点到隐藏层第j节点的连接权重,θj是第j个隐含节点的偏置,Xi表示第i个输入.
(1)
2) 计算隐藏节点的输出数据.每一隐藏节点输出计算为
j=1,2,…,h.
(2)
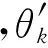
(3)
k=1,2,…,m.
(4)
多层感知最重要的是连接权重和偏置.在上述方程中看出,权重和偏置影响最终输出值.为了实际输出更接近期望输出,需寻找最佳的连接权重和偏置来训练多层感知机.
2 提取MLP输入数据
2.1 颜色矩特征 颜色矩(CMs)能表达图像的颜色信息,因此可提取图像的CMs特征作为多层感知机的输入数据.CMs的提取步骤如下:
1) 提取色度、饱和度及亮度分量.将图像转换到符合人类视觉特征的HSV空间颜色模型,分别提取表示不同颜色的色度(hue)分量H、表示颜色的深浅的饱和度(saturation)分量S和表示颜色的明暗程度的亮度(value)分量V.
2) 对每个颜色分量求颜色矩.提取两个矩,分别为均值(Mn)和标准方差(Sd).数学定义分别为(5)和(6)式,其中i∈H、S、V,表示任一通道.Ii,j表示图像第i颜色通道中第j像素点的值,N是像素总个数.
(5)
(6)
3) 组合矩.图像颜色分量选取H、S和V,共3个颜色分量,每个分量有2个颜色矩,线性组合6个矩,得到对应图像的一个6维颜色矩特征.
2.2 降维梯度方向直方图特征 梯度方向直方图(HOG)[16]算法可提取图像形状特征,使用文献[17]中简化了分单元的细节的IHOG特征提取算法,并在此基础上使用主成分分析的方法降维,使维数约减到最佳维度,此方法记为降维梯度方向直方图(DHOG),操作步骤如图2.
1) 计算梯度.像素点(x,y)水平方向的梯度Gh(x,y)、垂直方向的梯度Gv(x,y)分别用(7)和(8)式计算:
Gh(x,y)=f(x+1,y)-f(x-1,y)∀x,y,
(7)Gv(x,y)=f(x,y+1)-f(x,y-1)∀x,y,
(8)
像素点(x,y)的梯度值及梯度方向θ(x,y)分别用(9)和(10)式计算:
(9)
(10)
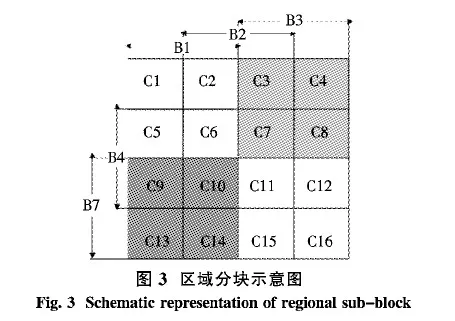
2) 分块.将分辨率为m*n像素的图像分为3×3块,分块时让相邻的区域有部分重叠,可使图像特征向量包含尽量多的信息.通过行步长⎣m/(3+1)」、列步长⎣n/(3+1)」,严格控制重叠块区域,使重叠部分大小为原区域的一半.图3为区域分块示意图.单元C1,C2,C5,C6组成块B1;单元C5,C6,C9,C10组成块B4;C5、C6为重叠区域.
3) 计算梯度直方图.对9个小块分别计算梯度直方图.首先每小块梯度方向范围取0°~180°,然后将其均分为9个方向角度,即0°~20°、21°~40°、
41°~60°等,最后结合式(9)、(10)计算出的结果分别统计在这9个方向角度的梯度值总和.
4) 归一化特征向量.对每一块的梯度直方图进行归一化能使特征向量空间对光照,阴影和边缘变化具有鲁棒性,选取L1-norm范式作为归一化函数,即式(11).其中,ν表示未归一化的特征向量,‖ν‖1为1-norm,ε为常数,为保证分母不为0,取值为0.01.
ν→ν/(‖ν‖1+ε).
(11)
5) 组合特征向量.将9块归一化后的特征向量线性组合,合成一个81维的特征向量.
6) 降维.为进一步获取步骤5)得到的特征向量的有效特征,利用主成分分析方法进行降维处理,选取得分率(方差贡献率)在89%以上的特征,得到最后降维梯度方向直方图.
3 BBO优化MLP
3.1 BBO算法基础 BBO的数学模型描述了物种种类在不同的栖息地迁入和迁出情况.图4所示为简单的物种迁移模型,在实际问题中则更复杂.横坐标代表物种种类,纵坐标代表比率.当物种种类为0时,迁入率λ最大,迁出率为0;S1迁入率大于迁出率,S2的迁入率低于迁出率.S1迁入率比S2的高,而迁出率比S2的低;当物种种类达到饱和的情况,迁出率最高,迁入率为0.当物种种类为S0时,迁入率等于迁出率,物种数量达到平衡状态,此时如出现突发疾病、贪婪捕食、自然灾害等情况,就需要花费较长时间恢复物种数量的平衡.
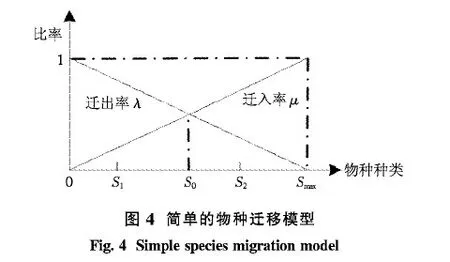
生物种群生活在不同的栖息地(Habitat),每个栖息地对应不同的栖息地适宜性指数(HSI).HSI越高,越适合物种居住.栖息地随着时间推移的规则为:居住在高HSI的种群,随着时间的推移此栖息慢慢地达到饱和,种群会迁出到低HSI的栖息地;低HSI的栖息地更容易吸引从高HSI栖息地迁出的种群;高HSI和低HSI的栖息地都可能面临一些突发情况,从而改变现有栖息地环境.BBO算法流程图如图5所示.
1) 生成初始栖息地.设定栖息地数量,栖息地内移民的最大容量,迁入率、迁出率函数的最大值I和E,最大的变异率mmax.
2) 计算所有栖息地的HSI.HIS按训练样本的均方误差(MSE)(12)式进行计算,即第i个栖息地的HIS值为(13)式计算所得.计算过后按HSI从高到低对栖息地排序.
(12)
HSI(Habitati)=E(Habitati),
(13)
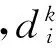
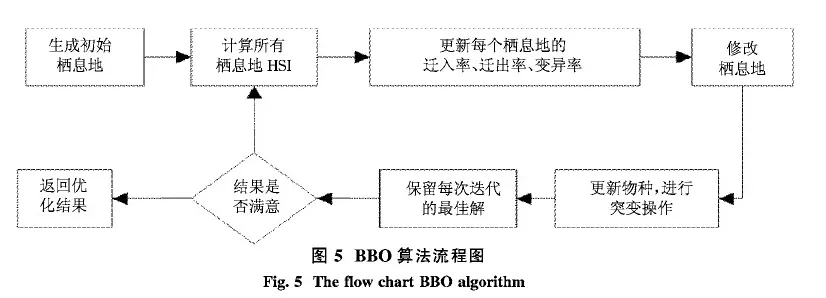
输出.
3) 更新每个栖息地的迁入率、迁出率、变异率.迁出率(μk)和迁入率(λk)数学定义为(14)、(15)式.N是栖息地上允许的最大移民数,n是栖息地上当前的移民数,E是最大的迁出率,I是最大的迁入率.
(14)
(15)
变异算子能保证栖息地尽可能呈现多样化的状态,从而增加搜索机会.数学定义为(16)式,其中M是由用户自定义的变异初始值,pn是第n个栖息地的变异率,
pmax=arg max(pn),n=1,2,3,…,N.
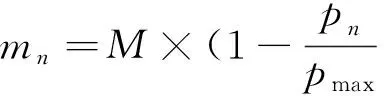
(16)
4) 修改栖息地.根据每个栖息地的迁入率和迁出率,移民按照迁移策略修改栖息地,并且重新计算HSI.
5) 更新物种,进行突变操作.执行步骤4)后,要重新计算每个栖息地的种群数量,根据变异算子,对非精英栖息地进行突变,并重新计算HSI.
6) 保留每次迭代最佳解.因突变会破坏较优方案的栖息地特征,所以在算法的迭代过程中,保留部分群体精英个体,这样能在HSI发生突变后,也能恢复到最佳解决方案.
7) 结果是否满意.此步骤主要看是否满足停止的条件,如不满足,则重回到第(2)步骤,满足条件则输出迭代最优解.
3.2 BBO训练MLP 学习的最终目的是训练1个多层感知机,使它能够识别测试集.
在学习阶段最重要的是训练集,每个训练样本应参与计算每个栖息地的HSI.
BBO训练MLP流程为首先产生1组随机MLP集作为栖息地,每个MLP对应1个栖息地,每个权重和偏置对应栖息地上的移民;由(12)式计算每个MLP的MSE;下一步是更新迁入率、迁出率和突变率;然后根据迁出率和迁入率重新选择MLP;根据突变率对MLP进行突变;具有较低MSE的解作为精英解保留;重复步骤,直到达到终止准则.
图6是BBO训练MLP的概念模型.

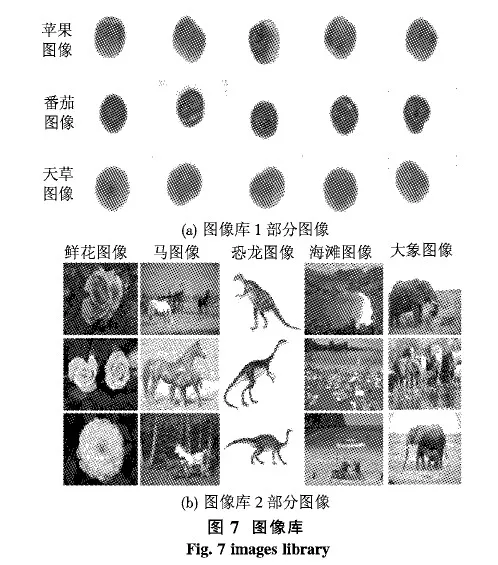
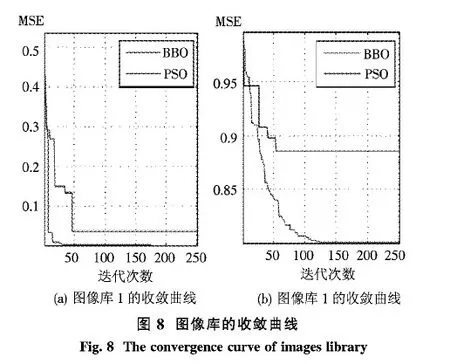
图示的4个栖息地的HSI高低为:HSI(Habitat1) 从图中可以看出,栖息地1具有最高的迁出率;栖息地4具有最高的迁入率,栖息地4接收来自栖息地1、栖息地2、栖息地3的移民,从而增加了权重和偏置;每一个栖息地都会发生突变. 4.1 实验设置 本文实验选用2个不同数量、类型的图像库,一个图像库为自制的水果图像数据库,定义为图像库1(如图7(a));另一个图像库选用文献[18]使用的部分Corel图像,定义为图像库2(如图7(b)).图像库1中的图像种类为3类,包括苹果、番茄和天草图像,均为128*128*3像素,JPG格式.每类图有50幅,一共有150幅图像;图像库2中的图像是选取Corel图像库的5类图像,包括鲜花、马、恐龙、海滩、大象,每类图像有100幅,共500幅.实验过程中训练集和测试集的组成为:图像库1中每类图像随机抽取20幅作为训练集,有3类图像,即一共选择60幅作为训练集,剩下的90幅图像作为测试集;图像库2中每类图像随机抽取30幅作为训练集,有5类图像,即一共选择150幅作为训练集,剩下的350幅图像作为测试集. 由于没有标准规则选择隐藏节点的数量,因此本文使用公式: 来定义隐藏节点数量,其中N表示输入数量,H表示隐藏节点数量. BBO算法中,每一个栖息地随机初始化的范围是[-10,10],步长为0.1;每个栖息地的最大移民数是200;移民率范围是[0,1];迁入率、迁出率最大值I和E均为1;为使变异率更切合实际,设置初始变异率为0,最大变异率为0.005;最大迭代次数为250次;精英栖息地设为保留2个. 4.2 特征提取实验 分别对图像库1及图像库2进行颜色矩特征、降维梯度方向直方图特征提取.根据2.1节介绍的颜色矩特征方法,分别得到图像库1及图像库2的颜色矩特征.根据2.2节介绍的DRHOG特征提取方法,首先图像库1及图像库2中的每一幅图像在第五步得到的特征向量为81维,然后进行步骤六的主成分分析降维处理,把得到的150*81、500*81维特征向量通过线性变换转成另一组不相关的变量,并使新的变量按照方差依次递减的顺序排列.数学变换保持变量的总方差不变,使第一变量具有最大的方差,称第一主成分,第二变量的方差次大,并和第一变量不相关,称为第二主成分.依次类推,81个变量就有81个主成分.接下来确定要提取的主成分的数量,选取方差贡献率在89%以上的特征.图像库1前10个主成分的方差贡献率达到90.67%;图像库2前10个主成分的方差贡献率达到89.51%,因此图像库1和图像库2的提取的主成分的数量均取10,由此得到每一幅图像的DRHOG特征. 表1是原始HOG(文献[16]使用的HOG方法)和DRHOG的对比数据表,特征维数表示对一幅图像进行相应特征提前后得到的特征具有的维数;时间表示一幅图像进行特征提取所耗时间. 表 1 原始HOG和DRHOG对比 表1所示DRHOG相比原始HOG特征,特征维数降低378倍,特征提取时间却少0.1 s.DRHOG算法继承了原始HOG描述子能描述图像局部形状信息、一定程度上抑制平移和旋转影响等优点的基础上,简化了分单元的细节,且利用主成分分析的方法降维,选取方差贡献率在89%以上的特征,使得DRHOG具有用尽量少的维数表示尽量多的形状信息的功能. 分别得到图像库1和图像库2的颜色矩和DRHOG特征后,线性组合这两个特征,得到每幅图像的一个16维组合特征,即有16个输入节点,采用的隐藏节点数量为33.图像库1的多层感知机结构为16-33-3;图像库2的多层感知机结构为16-33-5. 4.3 优化实验 为验证BBO算法训练多层感知机(BBO_MLP)用作图像分类的有效性,利用文献[19]中的粒子群优化算法训练多层感知机的方法(PSO_MLP)分别对图像库1和图像库2进行对比实验.实验结果如表2,分类准确率代表10次平均分类准确率.PSO初始参数中粒子数为200;最大迭代次数为250次;惯性权重取值0.3;社会学习因子和认知学习因子均取值为1;采用全连接型拓扑结构. 表 2 不同图像数据库分类准确率比较 Table 2 The comparison of classification accuracy in different image databases % 迭代次数图像库1分类准确率BBO_MLP PSO_MLP图像库2分类准确率BBO_MLP PSO_MLP1051.3341.3319.8017.402062.0048.6730.8024.203076.0064.6740.6037.0050100.0085.3364.2051.20100100.0085.3377.4065.80250100.0085.3384.2065.80 从表2数据可知,对于图像库1,迭代次数为10时,BBO_MLP的分类准确率为51.33%,PSO_MLP的分类准确率为41.33%.迭代次数为20时,BBO_MLP的分类准确率为62.00%,PSO_MLP的分类准确率为48.67%.随时迭代次数的增加,BBO_MLP和PSO_MLP的分类准确率逐步上升高或趋于稳定.当迭代次数到达250的时候,BBO_MLP和PSO_MLP的分类准确率达到较高精度,几乎能够对图像库1的图像进行精确分类.对图像库2,横向来看,相同迭代次数下BBO_MLP分类准确率稍高于PSO_MLP的分类准确率,如迭代次数为20时,BBO_MLP的分类准确率为30.80%,PSO_MLP的分类准确率为24.20%.纵向上来看,随时迭代次数的增加,BBO_MLP和PSO_MLP的分类准确率都呈现上升趋势.如BBO_MLP方法下,迭代次数100的分类准确率为77.40%,迭代次数250的分类准确率为84.20%. 4.4 优化实验结果分析 图像库1和图像库2的结果存在差异的原因如下. 1) 测试图像规模不同.图像库1的测试图像一共150幅,而图像库2的测试图像有500幅. 2) 测试图像类别数量不同.图像库1的测试图像类别为3类,图像库2有5个类别. 3) 图像内容不同.图像库1种类为苹果、番茄和天草,本文使用颜色矩和DRHOG特征作为MLP的输入数据,而这3类图像最显著的特征就是颜色不一致,形状差异相对较小,因此使用颜色矩和DRHOG特征用作图像库1的BBO_MLP、PSO_MLP分类准确率相对较高;图像库2种类为鲜花、马、恐龙、海滩、大象,图像内容相对较复杂,具有类内颜色多变,类间颜色相似,颜色特征差异较图像库1小,而形状特征也受背景差异、前景个数不一致的影响使形状特征差异表现不显著.因此整体上来看,相同迭代次数下图像库的分类率图像库1高于图像库2. BBO_MLP和PSO_MLP方法对同一图像库分类准确率不同,主要原因是BBO优化算法的收敛速度优于PSO优化算法.图8为图像库1和图像库2的收敛曲线.由图8可知,不管是图像库1还是图像库2,BBO优化算法的收敛速度较PSO优化算法快. 除了BBO_MLP收敛速度比PSO_MLP快之外,BBO_MLP方法计算复杂度较PSO_MLP方法小,BBO_MLP方法一次迭代平均运行时间为1.34 s,而PSO_MLP方法一次迭代平均运行时间为1.45 s. BBO算法是一个具有高收敛速度、较低计算复杂度、能避免局部极小的优化算法.由于它具有迁移和突变策略,所以能避免局部极小问题.PSO算法高度依赖于初始种群的分布,主要依靠是群体成员之间的吸引力来运动.如果许多粒子陷入局部最优,算法不能防止其他粒子也被吸引到局部最优位置,因此大部分粒子都被困在同一局部最优.BBO算法相比PSO算法具有更多的随机性,可根据突变策略不停的探索全局最优解,避免局部最小值问题,可解决复杂数据集的优化问题. 本文提出了面向图像分类的多层感知机BBO优化方法,能对不同种类的图像进行分类识别.在特征提取部分,采用颜色矩和DRHOG的组合特征,使得分类依据相对充分.在特征优化部分,通过采用BBO优化算法解决了MLP的连接权重和偏置的优化问题.为验证BBO优化算法优于其他优化算法,采用了PSO优化算法进行对比实验,实验表明BBO优化算法的收敛速度优于PSO优化算法,BBO优化算法训练MLP的计算复杂度低于PSO优化算法.实验采用2个不同数量规模、不同区分内容的图像库进行对比分析,验证了基于BBO优化的多层感知机分类方法的有效性.由于实验图像库1和图像库2的差异,实验采用的颜色矩和DRHOG特征并不能满足相对较复杂图像库2的分类识别需要,下一步将在此基础上,针对多种类多容量的大数据集图像库进行特征提取研究,采取适合的特征向量作为MLP的输入数据,进行BBO-MLP分类识别. 致谢 四川师范大学优秀论文培育基金(校研字[2014]7号28)对本文给予了资助,谨致谢意. [1] Dalal N, Triggs B. Histograms of oriented gradients for human detection[C]//IEEE Computer Society:CVPR 2005.2005,1:886-893. [2] Ryu S J, Kirchner M, Lee M J, et al. Rotation invariant localization of duplicated image regions based on Zernike moments[J]. IEEE Transactions Information Forensics and Security,2013,8(8):1355-1370. [3] Reddy R, Reddy B E, Reddy E K. Classifying similarity and defect fabric textures based on GLCM and binary pattern Schemes[J]. Inter J Infor Engin Electronic Business,2013,5(5):25-33. [4] Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transactions Pattern Anal Machine Intelligence,2002,24(7):971-987. [5] 丁学东,刘渊,谢振平. 增量学习语义属性的图像内容检索系统增强[J]. 计算机应用研究,2014,31(1):273-276. [6] 张俊才,张静. 使用粒子群算法进行特征选择及对支持向量机参数的优化[J]. 微电子学与计算机,2012,29(7):138-141. [7] 靳玉萍,李保霖. 基于遗传优化径向基概率神经网络的岩性识别应用[J]. 计算机应用,2013,33(2):353-356. [8] Simon D. Biogeography-based optimization[J]. IEEE Transactions Evolutionary Computation,2008,12(6):702-713. [9] Ma H, Simon D. Biogeography-based optimization with blended migration for constrained optimization problems[C]//Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation.ACM,2010:417-418. [10] Rahmati S H A, Zandieh M. A new biogeography-based optimization (BBO) algorithm for the flexible job shop scheduling problem[J]. Inter J Advanc Manufact Technol,2012,58(9/10/11/12):1115-1129. [11] Lozovyy P, Thomas G, Simon D. Biogeography-based optimization for robot controller tuning[C]//Comput Model Simul Intell:Current State and Future Perspectives,2011:162-181. [12] Rarick R, Simon D, Villaseca F E, et al. Biogeography-based optimization and the solution of the power flow problem[C]//IEEE International Conference SMC 2009:1003-1008. [13] Ho Y C, Pepyne D L. Simple explanation of the no-free-lunch theorem and its implications[J]. J Optim Theory Appl,2002,115:549-570. [14] Choudhari C S, Jain V. An Optimum Decision Making in Cognitive Radio via Fuzzy Neural Network[J]. Inter J Engineer,2012,1(5):1-7. [15] Kruse R, Borgelt C, Klawonn F, et al. Multi-Layer Perceptrons[M]. London:Springer-Verlag,2013:47-81. [16] 叶林, 陈岳林, 林景亮. 基于 HOG 的行人快速检测[J]. 计算机工程,2010,36(22):206-210. [17] 朱黎辉, 李晓宁, 张莹, 蒲华秀, 吴纯洁. 基于形状特征及纹理特征的中药材检索方法[J]. 计算机工程与设计,2014(11):3903-3907. [18] Zhang Z, Gu X, Kung S. Color-frequency-orientation histogram based image retrieval[C]//IEEE International Acoustics,Speech and Signal Processing,2012:1321-1324. [19] Peterson L E. Covariance matrix self-adaptation evolution strategies and other metaheuristic techniques for neural adaptive learning[J]. Soft Computing,2011,15(8):1483-1495. (编辑 陶志宁) BBO Optimization Method for Image Classification Based on Multi-layer Perceptron ZHU Lihui, LI Xiaoning In order to improve the accuracy of image classification decisions with the MLP’s weight and bias optimization, a BBO method for image classification based on multi-layer perceptron is proposed by borrowing from the thought of biogeography based optimization. Firstly, The combination of image features color moment and dimension reduction histogram of oriented gradient is extracted, then put to multi-layer perceptron as input datas. Secondly, BBO method is used to obtain the optimal weights and bias in 250 iterative times. Lastly, the test image’s category is obtained with multi-layer perceptron.This method can avoid algorithm being premature convergence and enhance the capability of image classification. With simulation experiments, compared with the method of particle swarm optimization, the higher quality and efficiency of this method is verified. Furthermore, the feasible scheme for image classification is also provided . biogeography based optimization; multi-layer perceptron; color moments; dimension reduction histogram of oriented gradient; particle swarm optimization 2014-09-03 四川省应用基础计划(2013JY0086)和四川省科技创新苗子工程基金(20132033) TP391 A 1001-8395(2015)06-0930-08 10.3969/j.issn.1001-8395.2015.06.026 *通信作者简介:李晓宁(1972—),男,副教授,主要从事图像处理和模式识别的研究,E-mail:lxn@sicnu.edu.cn4 实验与分析


5 结语
(CollegeofComputerScience,SichuanNormalUniversity,Chengdu610101,Sichuan)
