一类具有唯一奇点的3D混沌系统的反馈控制
2015-04-24赵汇涛赵苗婵
赵汇涛,赵苗婵
自从1963年Lorenz发现第一个混沌吸引子以来,混沌及其应用成为非线性科学研究领域中的一个热点问题.混沌是存在于自然界中的一种普遍现象,是在确定系统中产生的不规则运动.人们在认识和研究混沌理论和应用的过程中,逐步认识到混沌的研究价值和应用价值.由于混沌在生态系统、电子电路、计算与信息工程等领域有着广泛的应用,混沌的控制与应用得到了各领域研究者的广泛关注,并在现代控制方面取得了一系列研究成果.1990年,Ott等人提出了著名的OGY控制方法,由此引发了混沌控制的研究热潮,各种新的控制方法不断涌现,如自适应控制、滑模控制、脉冲控制与反馈控制等[1-4].其中由于混沌的反馈控制具有完善的理论基础,便于定量分析和设计,因而在近年来提出的众多控制策略中大部分都是反馈控制方法,如自适应控制、延迟反馈控制、追踪控制、模糊控制等[5,6].反馈控制可以使系统稳定于平衡点或不稳定周期轨道,甚至追踪任意的参考信号.
本文将考查以下系统
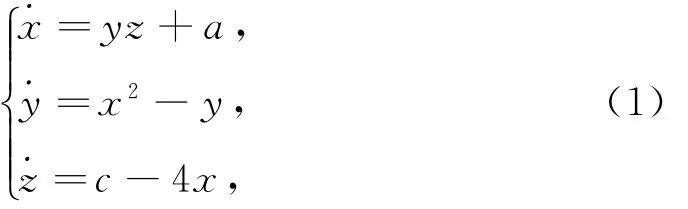
其中,x,y,z为系统的状态变量,a,c为系统的控制参数.当a=0,c=1时,系统(1)即为Sprott E系统[7],此时系统会出现混沌现象(如图1).而 Wang等[8]研究了当c=1时系统(1)的动力学行为,发现当参数a在某个范围内取值时,系统具有唯一的稳定的平衡点,但此时系统仍然会出现混沌现象.
下面将进一步讨论系统参数变化时对系统的动力学行为的影响,并利用时滞反馈控制方法对系统(1)产生的混沌现象进行控制.

图1 系统(1)在a=0时的轨线与相图
1 平衡点的稳定性与Hopf分支
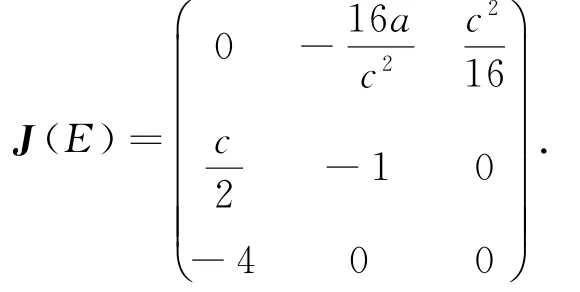
其特征方程为:

由Routh-Hurwitz判据可知方程(2)的特征根全部具有负实部的充要条件是:ac>0.

由方程(3)可得a=a0=0时ω=.设λ=λ(a),且满足λ(0)=iω0.方程(3)两边同时对a求导可得 Reλ'(0)=,则当c≠0时,横截条件成立,从而下面结论成立.
定理1 对系统(1),有
(i)若ac>0,则系统(1)的平衡点E是局部渐近稳定的;
(ii)若c≠0,则当参数a变化经过点a0=0时,在平衡点E处经历Hopf分支.
2 线性反馈控制

显然,系统(4)与系统(1)具有相同的平衡点E.系统(4)在平衡点E处的特征方程为

下面讨论受控系统(4)的Hopf分支.取K为分支参数且假设±iω(ω>0)为方程(5)的一对纯虚根,则ω满足以下方程

由式(6)可知,若C>0,则当A>0,B>0时,分支点K=K0满足方程AB-C=0.且由式(5)与(6)易知:sign(Reλ'(K0))=sign(-a(B-2A)).由于当K=0时,方程(5)即为方程(2),则由定理1,当ac>0时,平衡点E为渐近稳定的.则由以上讨论可得定理2.
定理2 对系统(4),有
(i)若A>0且AB-C>0,则系统(4)的平衡点E是局部渐近稳定的;
(ii)若B-2A>0,则当参数K变化经过点K0时,在平衡点E处经历Hopf分支(其中K0由方程AB-C=0所确定).
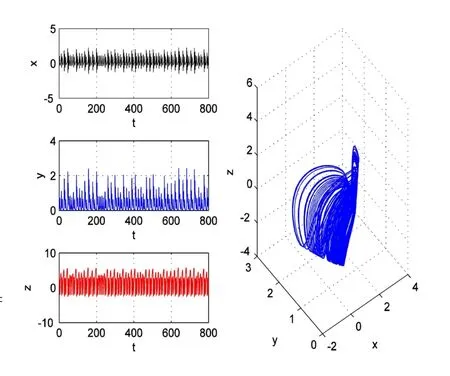
图2 初值为(0.25,0.01,0.01)系统(1)在a=-0.005时的轨线与相图
3 数值模拟
首先在系统(1)中取参数c=1,由上述讨论可知,当a<0时,平衡点E是不稳定的(见图2);当a>0时,平衡点E是局部渐近稳定的.且由文献[8]可知,当参数a取某些值时,系统(1)会出现稳定的平衡点与混沌吸引子共存的情况.例如,取a=0.005时,取初值为(1,1,1),则系统(1)的运动轨迹呈现混沌状态(见图3(a));取初值为(0.25,0.01,0.01),系统(1)的运动轨迹趋近于平衡点E(见图3(b)).当a=0时,系统(1)会有周期轨从平衡点E处分支出来,但此时仍然会有混沌现象出现.图4显示初始值为(1,1,1),则系统(1)的运动轨迹呈现混沌状态(见图4(a));当初值为(0.25,0.01,0.01),则系统(1)于平衡点E处分支出周期轨(见图4(b)).
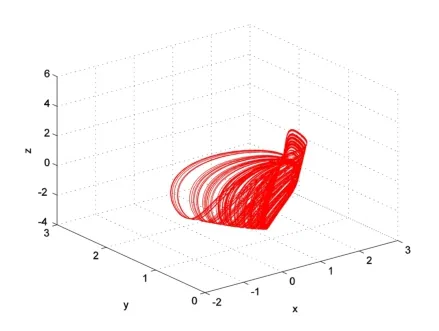
图3 (a)初值为(1,1,1)系统(1)在a=0.005时的相图

图3 (b)初值为(0.25,0.01,0.01)系统(1)在a=0.005时的相图
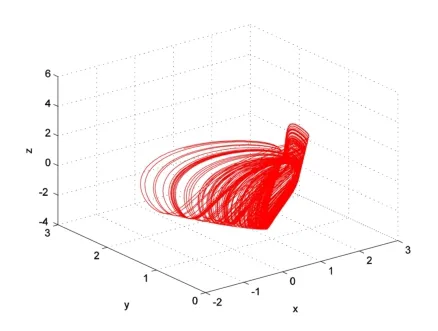
图4 (a)初值为(1,1,1)系统(1)在a=0时的相图
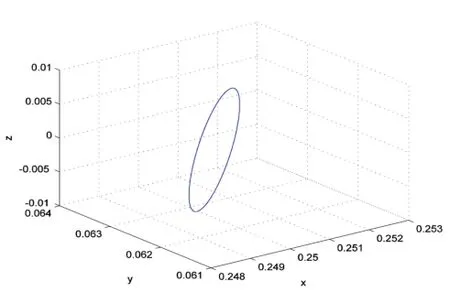
图4 (b)初值为(0.25,0.01,0.01)系统(1)在a=0时的相图
下面在系统(4)中取a=0.005,c=1,此时系统(4)有唯一的平衡点,由第二节的算法可得:
K10=0.031 791 226 42,K20=1.258 208 774,且sign(Reλ'(Ki0))=sign(1.71-Ki0)>0.于是当K<K10时,平衡点E是渐近稳定的;当K>K10时,平衡点E为不稳定的.且当K经过K10时,有周期轨从E处分支出来.但是受控系统(4)与未受控系统(1)有一个类似的现象是仍然会出现稳定的平衡点或周期轨与混沌吸引子共存的现象,下面的数值模拟也证实了这一情况.
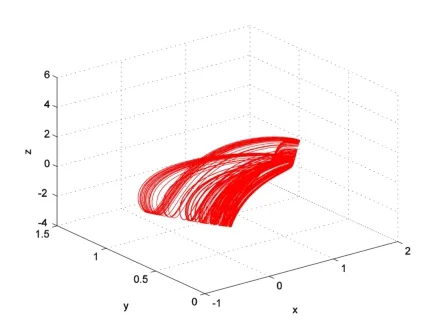
图5 (a)初值为(1,1,1)系统(4)在a=0.005,K=0.02时的相图
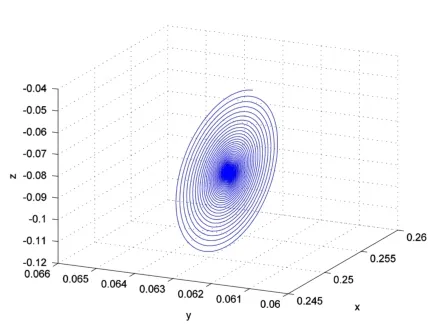
图5 (b)初值为(0.24,0.01,0.01)系统(4)在a=0.005,K=0.02时的相图

图6 (a)初值为(1,1,1)系统(4)在a=0.005,K=0.0315时的相图

图6(b)初值为(0.25,0.01,0.01)系统(1)在a=0.005,K=0.0315时的相图
图5 说明当a=0.005,K=0.02时,若取初值为(1,1,1),则系统的轨线呈现混沌状态(见图5(a));若取初值为(0.24,0.01,0.01),则系统的轨线趋于平衡点E(见图5(b)).
图6说明当a=0.005,K=0.031 5时,若取初值为(1,1,1),则系统的轨线仍呈现混沌状态(见图6(a));若取初值为(0.24,0.01,0.01),则系统的轨线趋于一个稳定的周期轨(见图6(b)).图7说明当a=0.005,K=0.04时,若取初值为(0.24,0.01,0.01),则平衡点E变得不稳定.
4 结论
本文讨论了一类具有唯一平衡点的自治系统.运用Hopf分支理论讨论了未受控系统(1)与受控系统(4)的平衡点的稳定性与Hopf分支.一个有趣的现象是,当选择的分支参数在临界点附近变化时,平衡点的稳定性会发生改变且会有周期解由平衡点分支出,但由数值模拟可以发现在未受控系统与受控系统中都会出现稳定的平衡点、周解轨与混沌吸引子共存的情况,而且当选择其他的控制方法,比如非线性反馈控制的时候,这种现象仍然存在,限于篇幅这里未能详细讨论,这也将是下一步的研究方向.

图7 初值为(0.24,0.01,0.01)系统(1)在a=-0.005,K=0.04时的轨线与相图
参考文献:
[1]Harb A M,AbdelP-Jabbar N.Controlling Hopf bifurcation and chaos in a small power system[J].Chaos.Solitons and Fractals,2003,18:1055-1063.
[2]Ghosh D,Chowdhury A R,Saha P.Bifurcation continuation,chaos and chaos control in nonlinear Bloch system[J].Communications in Nonlinear Science and Numerical Simulation,2008,13:1461-1471.
[3]Gohary A E,Ruzaiza A S.Chaos and adaptive control in two prey,one predator system with nonlinear feedback[J].Chaos,Solitons and Fractals,2007,34:443-453.
[4]Guan J.Bifurcation analysis and chaos control in genesio system with delayed feedback[J].ISRN Mathematical Physics,2012:1-12.
[5]Hwang C,Chow H,Wang Y.A new feedback control of a modified Chua's circuit[J].Physica D,1996,92:95-100.
[6]Vasegh N,Sedigh A.Chaos control via TDFCin time-delayed systems:The harmonic balance approach[J].Physics Letters A,2009,373:354-358.
[7]Sprott J.Some simple chaotic flows[J].Physical Review E,1994,50:647-650.
[8]Wang X,Chen G.A chaotic system with only one stable equilibrium[J].Commun Nonlinear Sci Numer Simulat,2012,17:1264-1272.
