类比思想在初中数学中的应用

叶金艳

摘要：本文重点阐述类比作为一种重要的数学思想方法是如何在初中数学教学实践中得到运用的，并在具体运用中又是如何潜移默化地影响学生拓展、创新思维方式，真正培养学生的科学精神。

关键词：类比;原则;方法

中图分类号：G427文献标识码：A     文章编号：1992-7711（2015）02-053-1

一、类比的含义

类比是依据两个对象之间存在着某些相同或相似的属性，推出它们存在其他相同或相似的属性的思维方法。一个类比包括目标问题和原问题两个部分。目标问题是需要解决的问题，原问题是已经解决的，并且是已经掌握的、比较常见、比较熟悉、比较形象具体、比较容易明白的问题。原问题与目标问题之间是平行关系，类比原问题解决目标问题，通过类比学会目标问题。初中数学教学中存在很多可以类比的知识与方法。

二、利用类比的策略

1.概念类比，理解本质辨异同。

对数学概念的正确理解是学好数学的基础，是培养学生思维能力的先决条件。在初中数学学习中有大量的概念，如果孤立地去理解与记忆这些概念，会成为学生学习的一个负担，但从概念的定义形式上看，有一部分概念的定义形式是相似的，通过这些概念之间的类比，进一步理解概念的本质。

例如：在学习一元一次方程、二元一次方程、一元二次方程时，我们可知只含有一个未知数，并且未知数的最高次数为1的整式方程叫做一元一次方程;只含有一个未知数，并且未知数的最高次数为2的整式方程叫做一元二次方程;含有两个未知数，并且所含未知数的项的次数都是1的方程叫做二元一次方程。从概念的定义形式上来看这里的“元”都是指未知数的个数，“次”指未知数的最高次数，只是未知数的个数和最高次数不同而已。通过这样的类比，学生能从同一个角度对这三个概念进行认识与理解，进一步理解这些概念的本质。

2.策略类比，讲究学法求效率。

学生对从已有的经验与知识出发来学习新知识的，在这一建构与认识过程中，类比起到了非常重要的作用，运用整体性解决问题策略类比的思想方法，能使学生轻松地掌握新的数学知识与方法，在探索中培养学生的创新思维，提高数学学习的效率。

在教学反比例函数时，采用整体解决问题类比的思想，把正比例函数、反比例函数图像性质作为原问题，教师引导学生自主探究、动手操作、合作交流，学习目标问题——反比例函数的图像与性质。正比例函数定义类比反比例函数定义、正比例函数的图像与性质类比反比例函数的图像与性质、正比例函数k值的几何意义类比反比例函数k值的几何意义、正比例函数的拓展应用类比反比例函数的拓展应用。在教学中渗透了类比思想，降低学生理解的难度，培养了学生的自主探索能力。

3.知识结构类比，构建网络促升华。

类比就是建立数学知识网络的一种有效的好方法，它能揭示这些知识之间的内在联系。数学知识只有构建成网络后，学生才能从更高的角度整体地理解复杂的数学知识。通过知识结构类比既能使知识得到横向拓宽，也能进行递进的纵向深化，鲜明地展示了知识的获取过程，形成清晰的知识脉络。

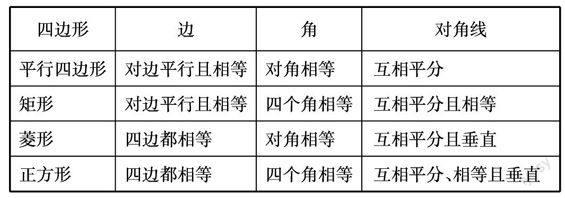
例如在讲解平行四边形的判定及性质时，我们引导学生把一般的平行四边形与矩形、菱形、正方形的性质列成表格进行知识结构类比，进一步明确它们之间的关系。

四边形边角对角线

平行四边形对边平行且相等对角相等互相平分

矩形对边平行且相等四个角相等互相平分且相等

菱形四边都相等对角相等互相平分且垂直

正方形四边都相等四个角相等互相平分、相等且垂直

通过上面的表格，对平行四边形、矩形、菱形、正方形从边、角、对角线三个方面进行类比，指出它们之间的相同之处，同时也理解它们之间的不同之处，从知识结构的角度来把握特殊四边形的性质，构建知识的体系与网络。要注意，类比不仅仅要关注“同”，也要关注“异”，“异”才是体现某一知识本质属性的东西。我们也可以通过纵向类比对所学的知识进行深化。

4.思维方式类比，突破难点会创新。

数学思维的呈现形式常常是隐蔽的，难以从教材中获取，这就要求教师在数学教学中有意识地、有目的地进行思维方法的渗透.通过数学思维的类比，不断在解决问题的过程中深化引导，学生的数学思维能力就会得到相应的提高。

在学完“三角函数”这一节后，我们可以出示下面的问题给学生研究，考查学生阅读能力、理解能力。通过学习三角函数，我们可知在直角三角形中，一个锐角的大小与两条边长的比值唯一确定，因此边长与角的大小之间可以相互转化。类似，我们可以在等腰三角形中建立边角之间的关系。我们定义：等腰三角形中底边与腰的比叫作顶角的正对（sad），在△ABC中，AB=AC，顶角A的正对记作sadA，这是sadA=底边腰=BCAB。容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解答下列问题：

（1）sad60°=。（2）对于0°<∠A<180°，

则∠A的正对值sadA的取值范围是。

“类比”既是一种思想，也是一种知识拓展策略。本题表面上是一种“新定义”型阅读理解题，其实是让学生类比锐角三角形的研究经验、方法，进而研究“顶角的正对值”问题。既有“顶角的正对值”的范围研究，也有“顶角的正对值”的应用，同时，将两个概念“整合”在一起，有助于考查思维的层次性，既考查了“化归”的数学思想，也考查了学生类比已学的知识解决实际问题的能力，培养学生创新的意识。