大位移井卡点预测实验

周劲辉， 张 勇， 高德利

(中国石油大学 石油工程教育部重点实验室，北京，102249)



大位移井卡点预测实验

周劲辉， 张 勇， 高德利

(中国石油大学 石油工程教育部重点实验室，北京，102249)

根据管柱扭转变形的特性，设计了8种水垂比情况下的大位移井管柱卡点预测实验，并对每种水平比下的管柱进行了3次扭转实验。对实验数据进行处理，用回归分析方法确定实际卡点位置与理论卡点位置的比值与水垂比间的函数关系，并建立基于剪切胡克定律的大位移井卡点预测计算式。结果表明：水垂比对大位移井管柱的加载特性有较大影响，它综合反映了管柱接头、管柱与井壁和套管的摩擦效应；未经修正的卡点计算公式平均相对误差达到24.67%，修正后的卡点预测公式的平均相对误差小于4.0%。建议应对大位移井摩阻扭矩进行分段计算。

大位移井； 管柱； 卡点； 预测

0 引 言

大位移井是水垂比λ(水平位移或测深与垂深之比)≥2的大斜度定向井或水平井，具有较大的水平位移。大位移井广泛应用于湖泊、滩海和浅海等油气资源的勘探开发。大位移井工程中经常发生井下管柱阻卡事故，对该类事故的处理耗时多、损失大，如何准确判断卡点深度是解决问题关键所在。通常，根据井下管柱被卡前后井下情况并结合经验来分析判断其性质。在现场确定卡点位置的方法主要有提拉法[1-8]、扭转法[9-10]和测卡仪测量法[11-16]。提拉法和扭转法分别利用材料力学的拉压胡克定律和剪切胡克定律，即金属材料在拉力(扭矩)作用下发生弹性形变时其所受的拉力(扭矩)与其伸长量(扭转角)成正比。有限元分析方法[17]和专家系统[18]也用来预测卡点。大位移井井下管柱在井眼中受到的摩阻力不能忽略，而大位移井中的摩阻力的计算又极其复杂。提拉法所建立的经验公式一般没有考虑摩阻力和管柱接头的影响，即使有的公式考虑了摩阻的影响，也是适应于直井或一般定向井，难以适合大位移井管柱卡点的精确计算。使用测卡仪确定卡点需要专门的技术人员，费用较高，仪器在大位移井中因摩阻原因一般难以下入，而且仪器也受地层磁场的干扰。因此，本文开展大位移井管柱卡点计算方法的研究具有实际意义。

1 实验原理

图1为空心等直圆杆在一定扭矩作用下的变形，根据剪切胡克定律：

(1)

式中：L为卡点深度(m)；G为材料切变模量，钢材一般取80 GPa；Ip为惯性矩(m4)；φ为扭转角(rad)；T为扭矩(N·m)。

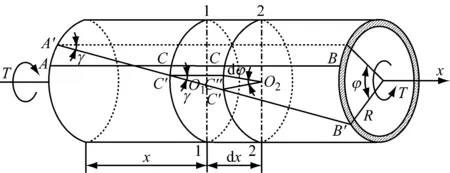
图1 空心等直圆杆在一定扭矩作用下的变形

等直圆杆的极惯性矩按下式计算：

(2)

式中：D、d分别为等直圆杆外、内径(m)。

2 实验设计

实验原理如图2所示，实验系统由模拟井筒、模拟管柱、扭矩扳手和转角表盘等组成。其中，模拟井筒有弯曲段和水平段，弯曲段形状为1/4圆，由不锈钢管法兰连接而成，其曲率半径为4 m、内径80 mm；水平段为模拟地层段，内径为25 mm，由水泥砂浆组成，可视为裸眼井段。模拟管柱由直径为12 mm，内径为9 mm的钢管组成，每根管柱长1 m，用螺纹连接。实验时，先将模拟管柱固定在设定的卡点位置，然后用扭力扳手在模拟管柱的扭矩加载端施加扭矩，使模拟管柱旋转一定的角度，记录此时的扭矩值和对应的旋转角度。重复上述步骤3次，分别取其平均值作为所加载的扭矩值及对应的扭转角。根据式(1)可以计算卡点以上管柱的理论长度。

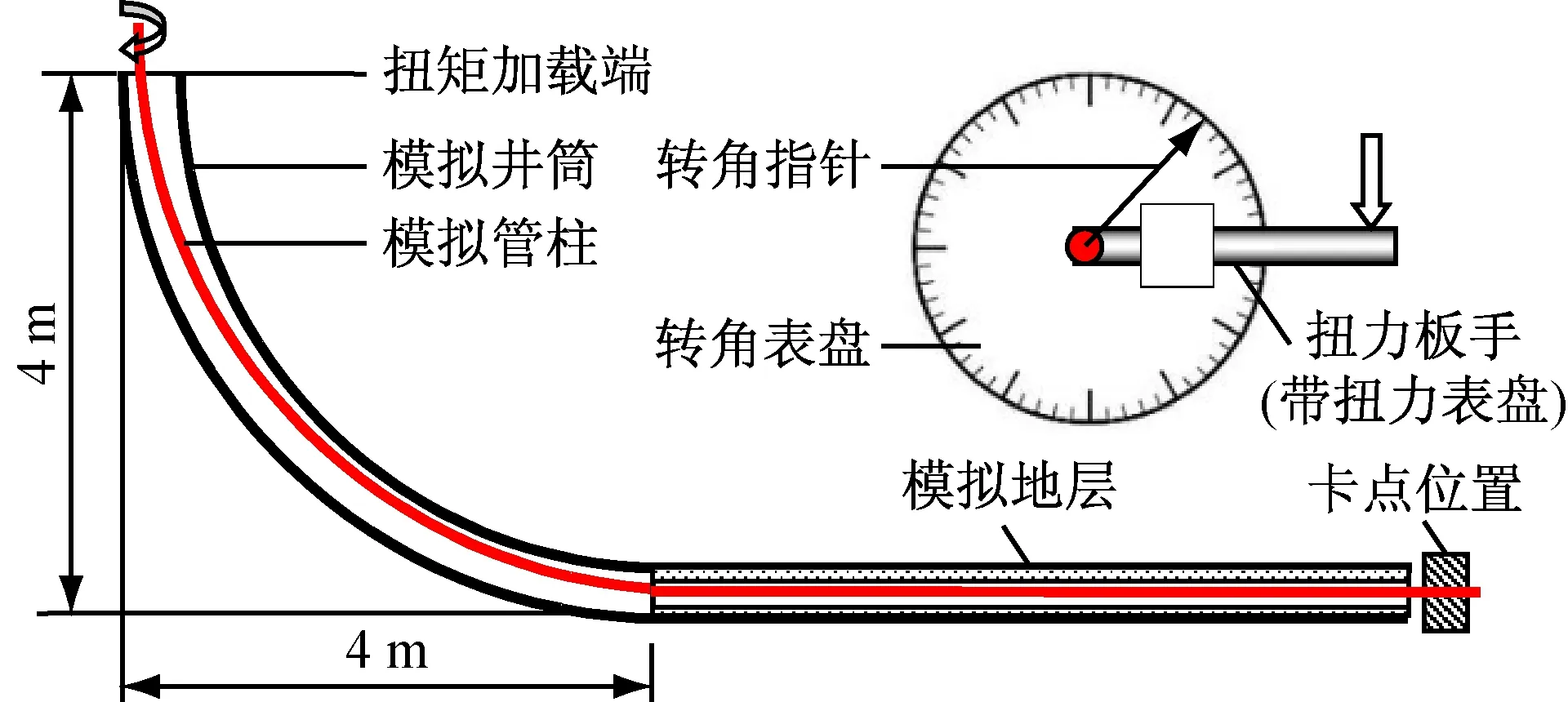
图2 实验原理

3 实验结果与分析

3.1 模拟管柱弹性参数的确定

用6根总长5.94 m的模拟管柱做了4组扭转试验来确定模拟管柱剪切模量，实验结果如表1所示。

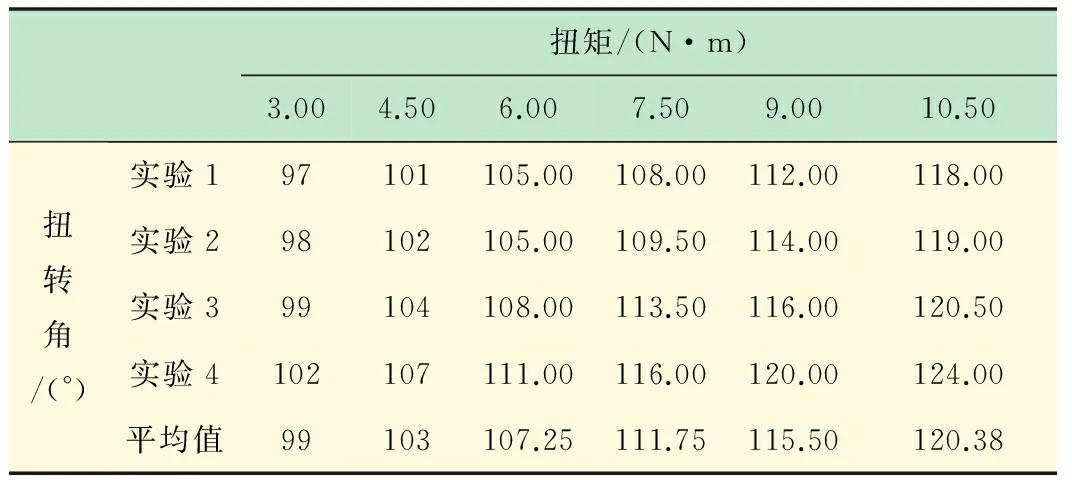
表1 计算模拟管柱剪切模量扭转实验数据

表中的扭转角代表表盘的读数，要知道在一定扭矩下所产生的扭转角必须对表1中的实验数据进行处理。将表1中的平均值转换成弧度，建立扭矩和扭转角之间的回归方程，将各平均扭转角值减去回归方程的截距(相当于清零处理)，得到如表2所示的数据。

由材料力学扭矩公式：φ=Tl/(GIp)，得G=Tl/(φIp)，其中：T/φ为表2中数据回归直线方程的斜率，不难求出其斜率为20.18。根据式(2)，可得Ip=1.39×109m4，由此求得管柱的剪切弹性模量为86.24 GPa。

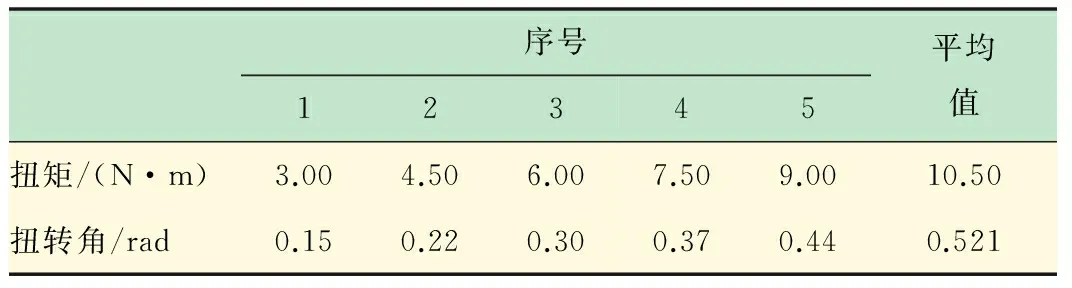
表2 模拟管柱剪切模量确定实验数据处理后结果

3.2 大位移井卡点实验

(1) 实验数据。水平段每次增加1根模拟管柱后做3次扭转加载实验，共进行了8组实验。每次实验均首先将扭矩加载到3 N·m，后续加载扭矩增量均为1.5 N·m，直到扭转困难为止(保持管柱弹性变形)。分别对每次实验的3组数据取平均值，得到如表3所示的实验数据。

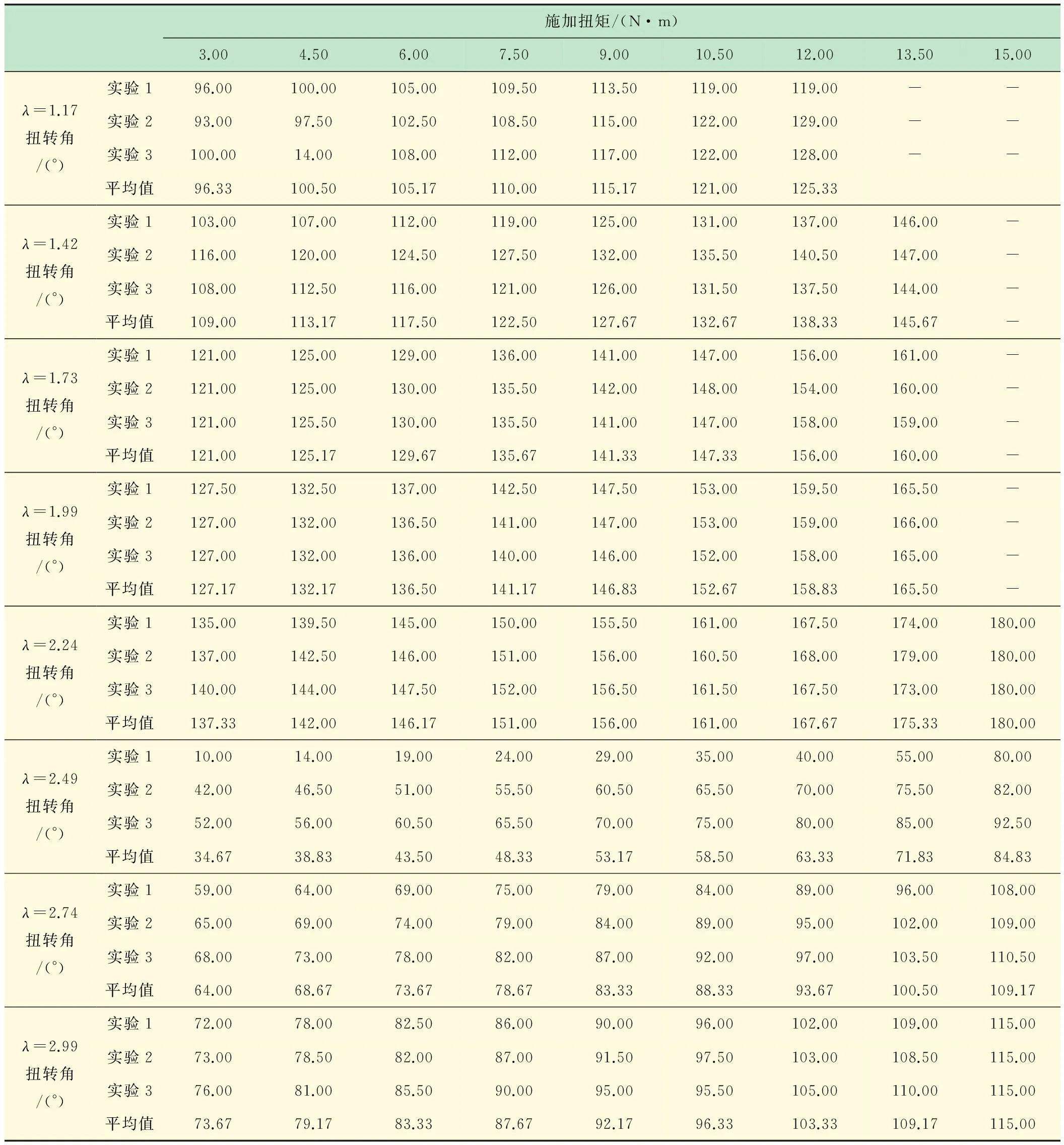
表3 不同水垂比(λ)下扭矩/扭转角实验数据

(2) 结果分析。对表3中不同水垂比下的扭矩和扭转角平均值进行回归分析，得到如图3所示的结果。从图中可以看出：在弹性变形范围内，管柱的扭转角随扭矩的增大基本呈线性变化规律。

表4是不同水垂比条件下理论卡点位置与实际卡点位置的对比。从表中数据可以看出，理论卡点位置与实际卡点位置的相对误差随着水垂比的加大而加大，相对误差绝对值平均达到24.67%；理论卡点位置普遍比实际卡点位置小。造成误差的主要原因之一是没有考虑管柱摩阻的影响，管柱摩阻抵消了部分扭矩的作用，导致同等扭矩作用下加载到管柱上实际扭矩减少了，扭转角变小，理论计算结果就偏小。且其变化规律与水垂比有一定的关系，因此在大位移井中进行摩阻扭矩预测时，根据不同的井段采用不同的计算模型比较合理[19-20]。

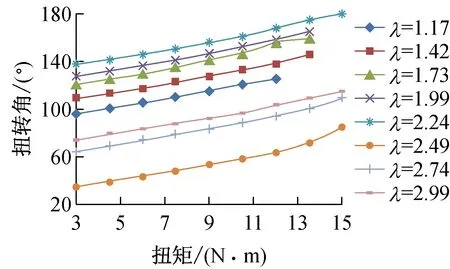
(a)清零前

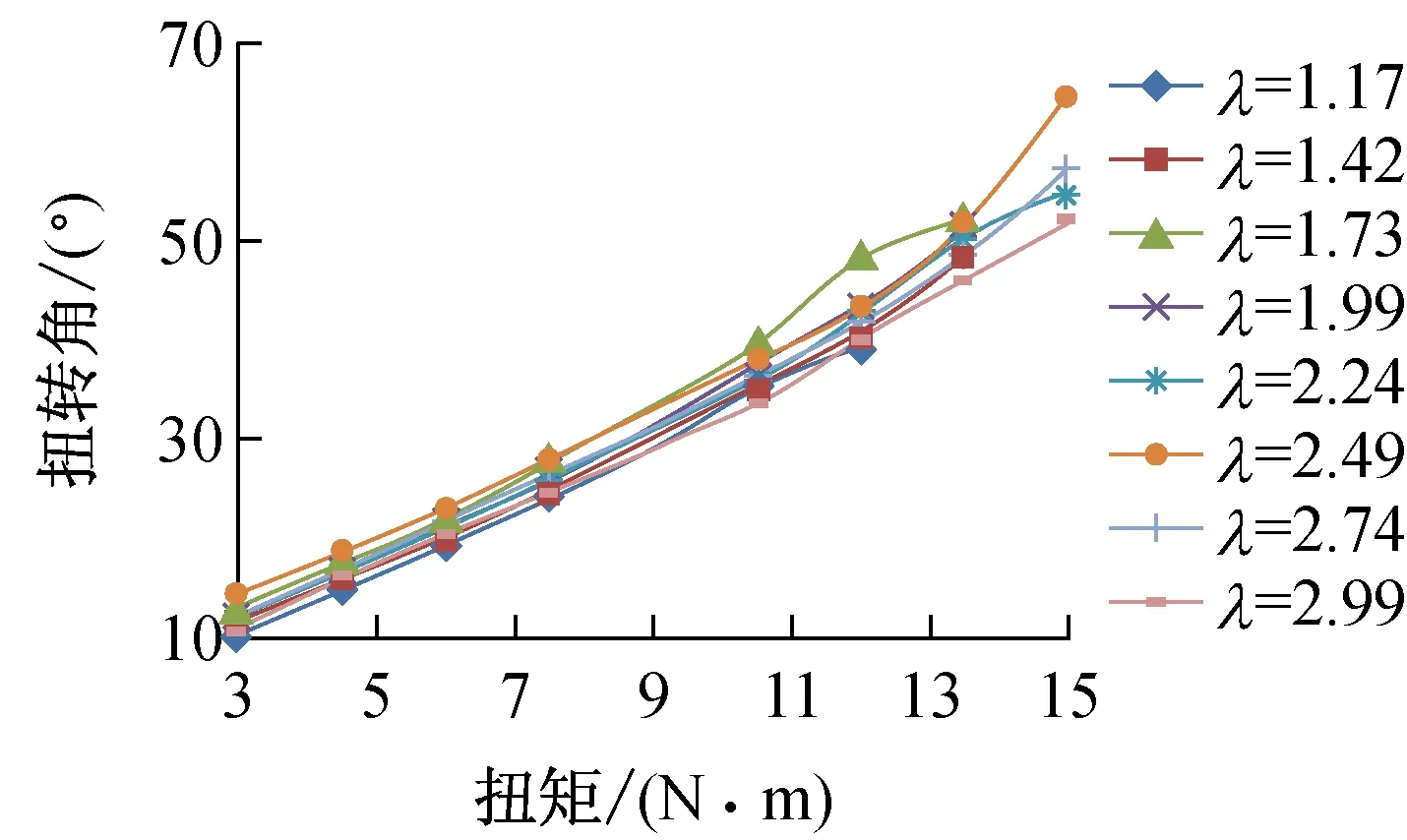
(b)清零后图3 不同水垂比下管柱扭矩/扭转角变化规律 表4 不同水垂比下理论卡点位置与实际卡点位置对比

λ1.171.421.731.992.242.492.742.99理论卡点位置/m6.877.198.077.577.528.127.577.07实际卡点位置/m6.637.698.909.9410.9411.9412.9413.94相对误差/%3.66-6.49-9.38-23.87-31.23-31.96-41.47-49.32

3.3 公式修正

实验表明[10]，扭转法可用于直井中卡点预测，但用于大位移井中，其误差较大。因此需对该方法的计算模型进行修正。

若实际卡点位置l与理论卡点位置l′的比为ε，修正后的卡点位置为l″，用回归分析的方法建立水垂比与误差比的回归方程，即ε=f(λ)，对于不同的λ，根据拟合的方程可以计算出相应的ε值，则

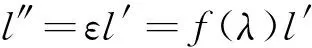
表5是根据上述修正方法对实验数据进行相关处理后的结果。分别用直线函数、二次多项式、三次多项式对水垂比与误差比的关系进行拟合，回归得到相应的拟合函数分别是：

ε=0.525λ+0.283

ε=0.179λ2-0.22λ+0.993

ε=0.125λ3-0.601λ2+1.326λ+0.03

从表5中的计算结果可以看出，相对误差绝对值平均分别为3.51%、3.13%和2.62%，比修正前的计算精度提高很多。各拟合函数的拟合效果如图4所示。

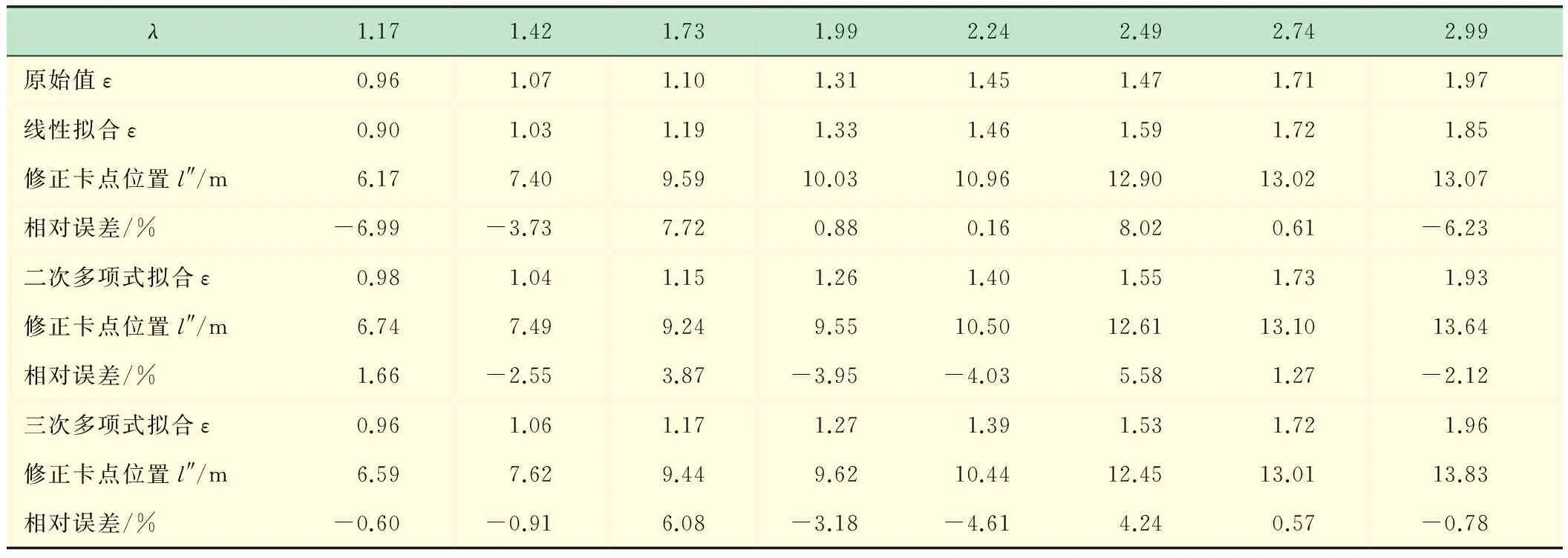
表5 大位移井卡点预测修正公式计算结果

4 结 语

利用管柱扭转变形特性(剪切胡克定律)可以预测大位移井管柱卡点位置。大位移井中的管柱摩阻对计算精度有较大的影响，建议对计算公式进行修正。模拟实验中，将实验管柱视为单一管柱，将管柱接头、管柱与井壁和套管的摩擦效应综合反映在水垂比中。修正前的计算误差达到24.67%，用直线方程、二次多项式和三次多项式分别进行修正，修正后的误差分别为3.51%、3.13%和2.62%。实验表明，水垂比影响管柱的加载特性，对大位移井摩阻扭矩计算时，建议进行分段计算。

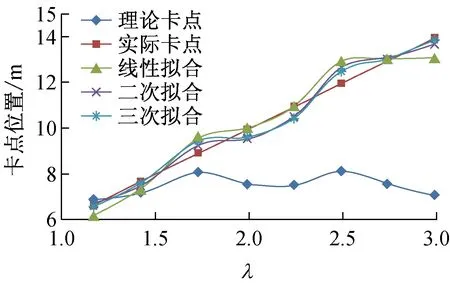
图4 拟合效果对比

[1] 冉津津，李长健，唐义祥，等. 油水井测卡点技术研究与应用[J]. 石油天然气学报(江汉石油学院学报)，2013， 35(5)：134-137.

[2] 渠有源，王孝山. 浮式钻井平台钻具卡点深度计算分析[J]. 海洋石油，2012，32(2)：95-97.

[3] 程 万，梅 杰，聂顶峰，等. 井下被卡管柱的卡点深度计算方法研究[J]. 长江大学学报(自然科学版)， 2011， 8(11)：44-47.

[4] 韩志勇. 卡点深度计算中消除摩阻力影响的方法[J]. 石油钻探技术，2010，38(1)：1-3.

[5] 宋德军. 管柱卡点计算[J]. 油气井测试，2008，17(1)：60-61，71.

[6] 刘东明. 井下被卡管柱的卡点公式计算法优化探讨[J].中国海上油气，2004，16(1)：83-85，94.

[7] 朱德武. 卡点计算公式的修正及其系数的确定[J]. 江汉石油学院学报，1991，13(1)：44-49.

[8] NEWMAN K R. Coiled-tubing stretch and stuck-point calculations

[C]//Congress SPE / ICoTA Coiled Tubing Roundtable: Houston TX. 25-26 May 1999：69-78.

[9] AADNOY B S，LARSEN K，BERG P C. Analysis of stuck pipe in deviated boreholes[J]. Journal of Petroleum Science and Engineering，2003，37(3-4)：195-212.

[10] 周劲辉，高德利, 王宇新. 钻柱卡点预测实验[J].实验力学，2010，25(5)：575-579.

[11] 王海东，欧跃强，陈 奂. 测卡、爆炸解卡技术在卡钻处理中的应用[J]. 石油工业技术监督，2013(8)：59-61.

[12] 黄河福，吴德麟. 测卡松扣系统在处理卡钻事故中的应用[J].石油钻探技术，1997，25(3)：90-92.

[13] PEID P I，MEETEN G H，WAY P W. Differential-sticking mechanisms and a simple wellsite test for monitoring and optimizing drilling mud properties[J]. SPE Drilling & Completion，2000，15(2)：97-104.

[14] 张景良，魏群涛. CQY2-I型测卡松扣仪研制及应用[J].石油矿场机械，2007，36(10)：37-38,48.

[15] SIEMS G，BOUDREAUX S. Applying radial acoustic amplitude signals to predict intervals of sand-stuck tubing[J]. SPE Production & Operations，2007，22(2)：254-259.

[16] GREY，KEVIN L. Method for determining a stuck point for pipe and free point logging tool[P]. US：7389183. 2008.

[17] 郭 凤，刘 合，张 劲. 卡点计算的有限元分析[J]. 机械工程学报，2007，43(1)：158-163.

[18] 陈明亮. 如何使用卡钻诊断与预测专家系统StuckES[J]. 钻采工艺，1999，22(5)：8-11.

[19] 秦永和，付胜利，高德利. 大位移井摩阻扭矩力学分析新模型[J]. 天然气工业，2006，26(11)：77-79.

[20] 闫 铁，李庆明，王 岩. 水平井钻柱摩阻扭矩分段计算模型[J]. 大庆石油学院学报，2011，35(3)：69-72，83.

Experimental Research on Prediction of Stuck-point of Downhole Tubular String in Extended Reach Well

ZHOUJin-hui,ZHANGYong,GAODe-li

(MOE Key Lab of Petroleum Engineering, China University of Petroleum, Beijing 102249, China)

Predicting stuck-point is one of the key techniques for releasing the downhole tubular string. It is more difficult to predict the stuck-point in extended reach well because of the long horizontal section, complex stress for tubular string and hard reaching for instrument of stuck-point detection. In terms of the characteristic of torsion deformation of tubular string, 8 kinds of experiments, which possess different ratios of horizontal displacement and vertical depth (λ), are designed to predict the stuck-point of tubular string in extended reach well. For each, torsion experiment of tubular string is carried 3 times. The function relationship between theoretical stuck-point and real one is set up with the method of regression analysis. The equation based on the Hook's law is established to predict stuck-point in the extended reach well. The experimental results show that the loading characteristic of pipe string is influenced by, and it reflects synthetically the friction effects of tubular string and their joints with the wall of well and casing. The average relative prediction error is 24.67% with the calculation equation which is not modified, and average relative prediction error is lower than 4.0% with the modified equation. It is suggested that the drag and torque should be calculated segmentally in extended reach well.

extended reach well; tubular string; stuck-point; predict

2014-07-14

国家自然科学基金创新研究群体项目(51221003)；国家863主题项目(2013AA064803)；国家自然科学基金联合基金项目(U1262201)；中国石油大学(北京)基金资助(KYJJ2012-02-45)

周劲辉(1971-)，男，湖南汨罗人，讲师，现主要从事井下力学/信息与控制工程理论与实验研究。

Tel.:010-89733087，18911226011；E-mail：ezhoujinhui@126.com

TE 242；P 634.4

A

1006-7167(2015)05-0011-05