基于层次熵的液压泵特征向量提取方法研究

， 　(军械工程学院 四系， 河北 石家庄　050003)

引言

液压泵是液压系统中的关键部件，其性能的好坏对整个液压系统操作的可靠性有重要影响。液压泵一旦发生故障，轻则振动、噪声增加，降低工作效率；严重时使液压泵不能工作，甚至会造成严重事故[1]。因此，有必要对液压泵进行故障诊断方法方面的研究，而特征向量提取是故障诊断中至关重要的一个步骤。

液压泵特征信号的选取非常关键，从合适的信号中可以充分提取特征，使故障诊断更准确。目前对液压系统进行故障研究可以选用的信号主要有：压力信号、流量信号、振动信号、温度信号和油液污染度。其中振动信号与液压泵的结构动态之间有着紧密的联系，最能反映液压泵状态，故本研究选取振动信号为特征信号。

故障液压泵在运行时，由于一些非线性因素，振动信号会表现出非线性特征[2]。这就导致传统的以线性系统为前提的时域和频域信号处理技术与小波变换理论都无法对液压泵的工作状态做出一个精确的评估。而非线性非平稳参数估计的发展为识别和预测复杂非线性非平稳问题提供了解决思路。例如，基于熵的参量已经被验证可以在时域上描述振动信号的非线性非平稳特征，并应用于故障诊断领域。Pincus[3]在研究婴儿猝死的心率变化时，提出了近似熵的概念。如今，近似熵已经成为了一种液压泵振动信号处理的工具，但近似熵存在自身匹配的缺点。针对近似熵的不足，Richman和Moorman[4]提出一种新的衡量时间序列复杂度的方法——样本熵。它具有对微小复杂性变化比较敏感和所需数据量少等优点，且已应用于婴儿心率变化分析。但是，熵值的增加并不意味着复杂度的增加，比如白噪声虽然样本熵值很大，但复杂度其实不高。为了解决这一问题，Costa[5]提出了多尺度熵的概念。多尺度熵在多个时间尺度上分析信号，一定程度上解决了样本熵在单一尺度上衡量时间序列复杂度所存在的问题，并已应用于生理学信号分析。

近几年，Jiang[6]提出一种层次熵的方法来衡量时间序列复杂度，通过层次分解和样本熵进行分析，并且已经将这种方法应用于心脏间隔时间序列，对不同的心脏疾病进行识别。和多尺度熵相比，层次熵的优势是，对于每个时间序列，它不仅考虑了其“低频”成分，同时考虑了“高频”成分。多尺度熵仅仅考虑了多尺度时间序列的低频成分，而特征信息很有可能就隐藏在“高频”成分。这对于从液压泵振动信号中提取特征信息是不充分的。Zhu[7]将层次熵与支持向量机结合应用于滚动轴承的故障诊断，取得了良好的效果。

考虑到层次熵在特征提取上的优点，本研究利用层次熵对液压泵端盖处的振动信号进行特征提取。首先利用层次分解方法对振动信号进行n=4的分解，将分解得到的8个节点信号样本熵作为特征向量输入支持向量进行模式识别，并与以样本熵和多尺度熵为特征向量的特征提取方法进行比较。实验数据比较结果验证了该方法的有效性。

1　样本熵特征提取和实例

1.1　样本熵介绍

给定一个时间序列X={x1,x2，…，xN}，其样本熵定义[6]如下。

(1) 构造m维向量Xm(i)：

Xm(i)={x(i),x(i+1),…,x(i+m-1)}，

1≤i≤N-m+1

(1)

(2) 向量Xm(i)和Xm(j)的距离定义为：

d[Xm(i),Xm(j)]=

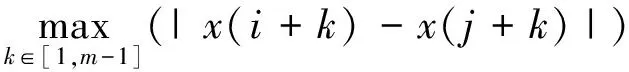
(2)

(3)

(4)

(5) 再构造m+1维向量Xm+1(i)，重复步骤1～4，得到Bm+1(r)，进而得到该序列的样本熵：

(5)

在计算样本熵时，本研究选取m=2，r=0.2SD(SD为原始时间序列的标准差)。

1.2　实验准备

本实验采用斜盘式轴向柱塞液压泵，其驱动电机的额定转速为1480 r/min。液压泵的柱塞数为7，理论排量为10 mL/r，额定转速为1500 r/min。将CA-YD-139型压电式加速度传感器安装在液压泵的端盖处，如图1所示。

图1　传感器安装位置

设置液压泵主溢流阀压力为10 MPa，采样频率为2 kHz，采样时间为50 s，采用DH-5920动态信号测试分析系统采集并存储数据。首先用正常状态下的液压泵进行实验，采集端盖处的振动信号，然后将正常部件替换成故障部件，人为模拟液压泵配流盘磨损、2个松靴故障和1个松靴故障的三种故障模式。

1.3　样本熵特征提取实例

分别从四种液压泵状态的振动信号上随机截取1024个点为样本信号，图2展示了各状态的时域波形。

根据图2，发现仅从时域波形上很难判断液压泵为何种状态，因此，需要对振动信号做进一步处理。分别计算图2中4种信号的样本熵，另再取两组不同的样本信号并计算其各状态的样本熵，再求取同一类别三组数据的平均值，结果如表1。

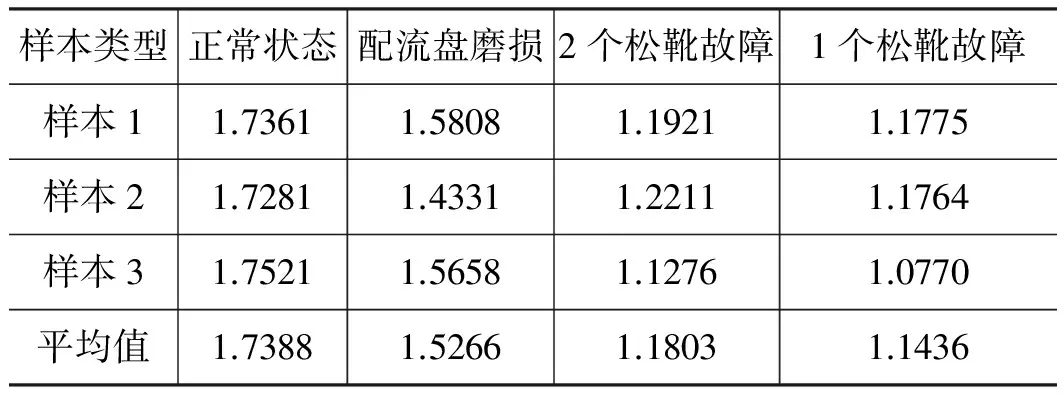
表1　液压泵四种状态的样本熵

设液压泵正常状态下的样本熵值为SE1，配流盘磨损下的样本熵值为SE2，2个松靴故障下的样本熵值为SE3，1个松靴故障下的样本熵值为SE4。从表1可以看出，液压泵不同状态下的样本熵值不同，同种状态下的样本熵值相差不大，四种状态下样本熵的关系为：

SE1>SE2>SE3>SE4

(6)

因为液压泵正常状态下的振动是随机振动，信号无规则程度较高，因而样本熵值较大。而对于存在故障的液压泵，在特定的频段有固有的冲击，因而无规则程度较低，样本熵值较低。另外，与配流盘接触的零部件较多，因而理论上配流盘磨损状态下的振动信号比松靴状态下要复杂，样本熵值较大。一般来说，2个松靴故障下的振动信号比1个松靴故障下的振动信号要复杂，所以熵值也较大。综上，样本熵可以实现液压泵不同状态的识别，但四种状态之间样本熵值差别不大。

将液压泵四种状态下的样本熵作为液压泵特征向量输入支持向量机。选取四种状态各60组，共240组数据作为训练样本，各15组，共60组数据作为测试样本。

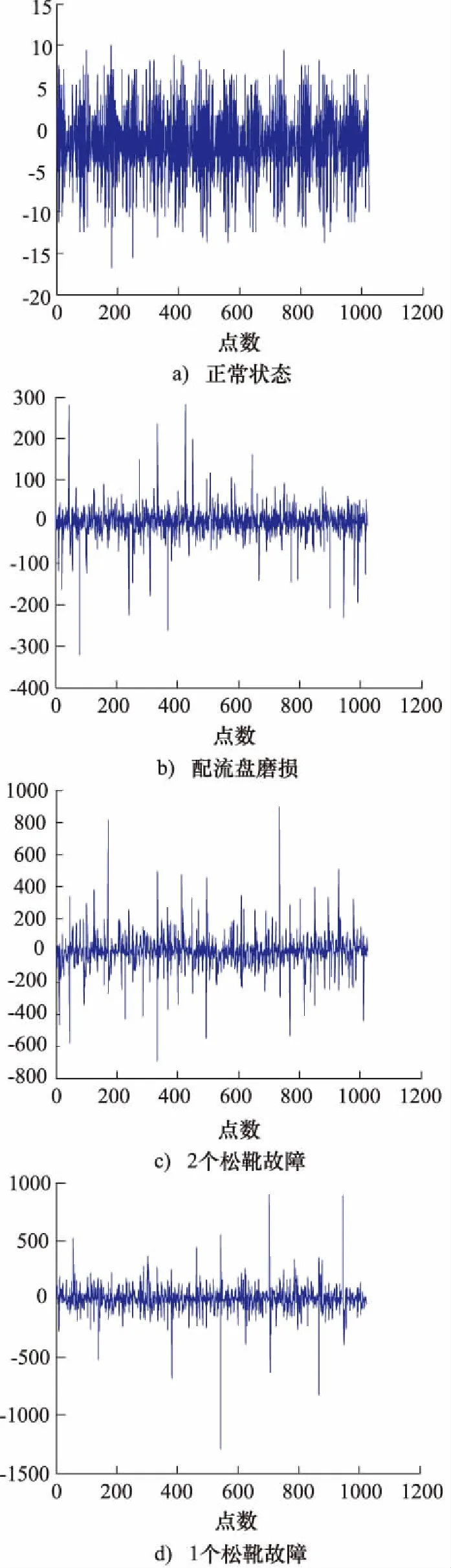
图2　四种状态的时域信号

经过支持向量机运算分类后，样本熵训练样本识别准确率为81.6667%，测试样本识别准确率为76.6667%。

2　多尺度熵特征提取和实例

2.1　多尺度熵介绍

给定一个时间序列X={x1,x2,…,xN}，其多尺度熵定义[6]如下。

首先对时间序列X进行处理，构造新的粗粒向量：

(7)

式中，τ为尺度因子，对于任意非零的τ，原始时间序列可以被构造成长度为n/τ的粗粒序列。当τ=1时，粗粒序列为原始时间序列。时间序列的粗点变化如图3所示。

图3　时间序列的粗点变化

分别计算重构后尺度为1～τ的τ个粗粒序列的样本熵，并绘制成关于尺度因子τ的函数，这个过程称为多尺度分析。

2.2　多尺度熵特征提取实例

用多尺度熵分别对图2四种信号进行处理，结果如图4所示。

图4　液压泵不同状态的多尺度熵

从图4可以看出，随着尺度的增加，四种状态的样本熵趋势是逐渐减小，但有轻微波动。正常状态的样本熵下降最快，其他三种状态在各尺度上的样本熵也大体可以维持SE2>SE3>SE4的大小关系。如此，就可以相对直观的区分液压泵四种状态了。

将经处理的液压泵四种状态下的多尺度熵作为液压泵特征向量，输入支持向量机。选取四种状态各60组，共240组数据作为训练样本，各15组，共60组数据作为测试样本。

经过支持向量机运算分类后，多尺度熵训练样本识别准确率达98.75%，测试样本识别准确率达96.6667%。

3　层次熵特征提取和实例

3.1　层次熵介绍

给定一个时间序列X={x1,x2,…,xN}，其中N=2n，其层次熵定义[6]如下。

首先定义一个均值算子Q0：

j=1,2,…,2n-1

(8)

长度为2n-1的时间序列Q0(X)表示原时间序列X经过一次层次分解后的低频成分。定义另一个算子Q1：

j=1,2,…,2n-1

(9)

长度为2n-1的时间序列Q1(X)表示原时间序列X经过一次层次分解后的高频成分。原时间序列X也可以由Q0(X)和Q1(X)表示：

x2j-1=(Q0(X))j+(Q1(X))j

x2j=(Q0(X))j-(Q1(X))j

j=1,2,…,2n-1

(10)

由此可知，时间序列Q0(X)和Q1(X)构成了对时间序列X在n=2时的层次分解。算子Qj(j等于0或1)可表示为一个矩阵：

(11)

算子Qj的矩阵形状取决于它们所作用的时间序列的长度。

为了描述X的多层次分析，这些算子将会被反复使用。令e为整数，且0≤e≤2n-1。令Li(i=1,2,…,n)等于0或1。对给定的e，有唯一一组向量[L1,L2,…,Ln]，使得：

(12)

序列X的层次分量定义为：

Xn,e=QL1,QL2,…,QLn(X)

(13)

由上述可知，Xn,0代表时间序列X在第n+1层的低频成分，Xn,1代表时间序列X在第n+1层与之相对应的高频成分。X0,0代表原时间序列X。对于不同的n和e，Xn,e构成了X在不同层次上的分解信号。事实上，所有Xn,0构成了对原时间序列X尺度为2n的多尺度分析。图5展示了X的层次分解图。

图5　n=3时的层次分解

最后，计算经过层次分解后节点信号Xn,e的样本熵，这个过程叫做层次熵分析。

3.2　层次熵特征提取实例

用层次熵分别对图2中四种信号进行处理，取n=4， 结果如图6。横坐标1～8代表层次分解节点X4,0～X4,7。

图6　液压泵不同状态的层次熵

从图6可以看出，各状态直观区别不明显。但液压泵4种状态的“高频”部分都有较高的样本熵值，这说明特征信息不仅隐藏在“低频”部分，还隐藏在“高频”部分，同时也说明了多尺度熵在衡量时间序列复杂度上的不完整性。

将经处理的液压泵四种状态下的层次熵作为特征向量，输入支持向量机。选取四种状态各60组，共240组数据作为训练样本，各15组，共60组数据作为测试样本。

经过支持向量机运算分类后，层次熵训练样本识别准确率达98.75%，测试样本识别准确率达98.33%，较多尺度熵有所提高。

4　结论

(1) 样本熵在衡量时间序列复杂度方面表现出诸多的优点，但不能解释白噪声熵值很大的问题，说明样本熵在衡量时间序列复杂度上存在不足。以样本熵值为特征向量，由于特征向量是一维向量，不利于分类，而且实验中各状态样本熵值相差不大，导致区分效果不明显，模式识别准确率偏低；

(2) 与样本熵相比，多尺度熵通过在多尺度上衡量时间序列复杂度，一定程度上降低了由于样本熵的不足带来的影响。由于特征向量从一维增至多维，而且各状态能直观区分，使得模式识别准确率大为提高；

(3) 层次熵与样本熵相比，其实也是一个特征向量从一维到多维的过程。与多尺度熵相比，层次熵在相同维数下对特征的提取更准确和完整。虽然层次熵不能直观区分液压泵各状态，但模式识别准确率最高。

综上所述，将层次熵应用于液压泵特征向量提取具有很好的效果，为液压泵的故障诊断或预测打下了良好的基础。该方法还为其他液压设备甚至机械设备的特征向量提取方法研究提供思路。

参考文献：

[1]唐宏宾,吴运新,滑广军,等.基于EMD包络谱分析的液压泵故障诊断方法[J]. 振动与冲击,2012,31(9):44-48.

[2]YANG Yu,YU De-jie,CHENG Jun-sheng. A Roller Bearing Fault Diagnosis Method Based on EMD Energy Entropy and ANN[J]. Journal of Sound and Vibration,2006,294(1-2):269-277.

[3]PINCUS S M. Approximate Entropy as a Measure of System Complexity[J]. Proceedings of the National Academy of Sciences,1995,88(6):2297-2301.

[4]RICHMAN J S,MOORMAN J R. Physiological Time Series Analysis Using Approximate Entropy and Sample Entropy[J]. Heart Circulatory Physiology,2000,278(6):2039-2049.

[5]COSTA M,GOLDBERGER A L,PENG C K. Multiscale Entropy Analysis of Biological Signals[J]. Physical Review E,2006,(71):1-18.

[6]JIANG Ying,PENG C K,XU Yue-sheng. Hierarchical Entropy Analysis for Biological Signals[J]. Journal of Computational and Applied Mathematics,2011,(236):728-742.

[7]ZHU Ke-heng,SONG Xi-geng,XUE Dong-xin. A Roller Bearing Fault Diagnosis Method Based on Hierarchical Entropy and Support Vector Machine with Particle Swarm Optimization Algorithm[J]. Measurement, 2014,(47):669-675.