基于遗传算法的旋塞阀液压缸缓冲优化研究
2015-04-16华中科技大学机械科学与工程学院湖北武汉430074
, , , (华中科技大学 机械科学与工程学院, 湖北 武汉 430074)
引言
电液操纵旋塞阀是蓄电池室的重要组成部分,可用于改变蓄电池室水冷管路中蒸馏水的流向。旋塞阀通过液压缸两端液压油推动缸内活塞齿条运动,带动四通塞芯上端的齿轮轴旋转,从而实现旋塞阀两个流向的转换。原旋塞阀方案在塞芯换向过程中液压缸活塞缓冲不充分,撞击噪声较大,对环境舒适性有很大影响。Simulink可对液压缸活塞运动学方程进行求解,得到活塞在缓冲过程中的运动学状态[1]。遗传算法运用生物进化的理念,对活塞缓冲的结构进行全局优化概率搜索,最终得到适应该工况且噪声低的缓冲结构。
1 旋塞阀液压驱动原理
液压缸活塞的缓冲方式采用在液压缸内部设计节流缓冲结构来实现缓冲,工作中,当活塞运动到节流孔中时,在活塞与节流孔之间形成环形间隙,排油腔内的液压油只能从环形间隙中流出,由于节流阻尼的作用,在排油腔内形成局部高压流体,活塞运动动能转换成油液压力势能从而迫使活塞减速达到缓冲的目的。缓冲原理图如图1所示,当该腔作为排油腔时,油液从节流缝隙中流出;而当该腔作为入油腔时,油液主要从单向阀中流过。
在活塞的运动过程中, 由于缓冲活塞和节流孔之间的距离不同从而造成的环形间隙不同,活塞缓冲根据不同的环形间隙得到不同的缓冲运动方程,将缓冲过程中的节流方式分为锐缘节流和缝隙节流[2]。缓冲节流过程如图2所示。

图1 缓冲原理图

图2 缓冲节流过程
针对液压缸活塞的缓冲工况,忽略油液的粘性阻尼和压缩性,得到液压缸的缓冲活塞的力学平衡方程以及流量方程[3]。力学平衡方程如下:
流量方程如下:
(1) 在缓冲活塞距离节流孔距离较远时,压力损失处于局部压力损失阶段:
(2) 缓冲活塞与节流孔之间的间隙逐渐变小,缓冲活塞进入锐缘节流阶段,当活塞未进入节流孔时:
当活塞进入节流孔时:
(3) 在活塞处于缝隙节流阶段时,分为锥形面节流和圆柱形面节流,当活塞处于锥形面节流时流量方程为:
在活塞处于固定节流口的圆柱形节流口时的流量方程为:
式中:m为活塞质量;v为缓冲活塞运动速度;p为液压缸供油压力;p0为液压缸进油腔内压力(p0=p-Δp);p1为排油腔内压力(p1=Δp);p2为缓冲腔内压力(p2=p1+Δp′);A1为系统油腔活塞截面积;A2为系统缓冲腔面积;A3为进出油孔面积;F为负载力;d为节流孔直径;δ为缓冲活塞与节流孔之间的间隙;Cd为流量系数;ρ为油液密度;μ为油液动力黏度。
2 Simulink仿真分析
针对活塞缓冲过程中的速度、加速度以及位移变化,采用MATLAB[4,5]软件中的Simulink软件包进行建模、仿真和分析,对缓冲过程中的流体速度、加速度运动微分方程进行仿真分析及求解。在Simulink模块中同时采用方块图输入和MATLAB语言编写M文件输入仿真模型,并且可以方便的修改仿真参数进行不同仿真过程的动态仿真。
建立力平衡方程和流量方程后,利用MATLAB/Simulink软件创建活塞缓冲模型方框图,如图3所示。由于活塞的缓冲速度,回油腔的压力对整个缓冲系统的动态特性有着很大的影响,因此对其阶跃响应进行仿真分析。
对于旋塞阀选择合适的缓冲结构需确定其缓冲缝隙、缓冲圆锥锥度、缓冲柱塞直径等设计参数。他们具有非线性、多目标、多约束的特点,利用遗传算法的全局搜索能力,简单通用、鲁棒性强的优点,以下对缓冲结构的参数进行遗传算法优化选择合适的设计尺寸,观察缓冲过程曲线。
如图4仿真结果所示,旋塞阀缓冲活塞直径一定d=20 mm 以及缓冲活塞圆锥段锥角一定δ1=0.9 mm,缓冲活塞和节流孔之间的缝隙不同时, 缝隙越小缓冲时间越长,缓冲末速度越小。但缝隙过小,缓冲时间太长不利于快速响应,缓冲末速度基本为0 ,可能出现缓冲活塞爬行现象,产生抖动。

图3 驱动方案的数学模型图

图4 液压缸缓冲速度-行程图
3 遗传算法求解优化
遗传算法[6,7]是基于生物进化过程中优胜劣汰的自然选择过程而形成的随机优化搜索算法。在计算过程中,遗传算法需要进行选择,以挑选满足目标条件的最佳适应度[8]。根据算子的适应度选择相适应的交叉变异。迭代收敛后得到近似最优解。
在缓冲过程中希望得到较低的末速度、合适的缓冲时长,平稳的缓冲过程以降低液压缸驱动过程中的噪声。运用此圆柱圆锥缓冲柱塞时,结构示意图如图5所示,缓冲过程中的变量包括缓冲柱塞的直径d、缓冲柱塞和节流孔间的间隙δ以及缓冲柱塞圆锥段的斜度高度差δ1,设定目标函数为缓冲时长t为最接近1 s以及末速度v最接近0。

图5 圆柱圆锥缓冲结构示意图
根据所建立的Simulink仿真模型,运用MATLAB软件中的M语言,打开其中的遗传算法模块,设置优化算法的各参数取值区间为:
0.8 mm<δ1<3 mm
0.05 mm<δ<0.25 mm
15 mm 通过51次迭代计算得到遗传算法的优化结果为: δ1=0.8 mm,δ=0.118 mm,d=20 mm 通过遗传算法求得的结果是近似最优解,多次求得的结果与其初始值范围有关,但都相差不大。多次执行该遗传算法求解,综合得到近似最优解[9]。 根据所得到的数学模型可以求得原方案下的以及新方案下的某一任意参数下的速度-时间曲线如图6和速度-位移曲线如图7。 图6 缓冲活塞速度-时间曲线 图7 缓冲活塞速度-位移曲线 根据缓冲计算所得到的缓冲时间为1.0076 s,缓冲末速度为0.0097 m/s。缓冲在一定时间内有效的降低了缓冲末速度,使得最终噪声减小。 基于旋塞阀的液压缸缓冲,运用MATLAB软件中的Simulink进行仿真分析,运用遗传算法的方法进行最优化分析,得到了旋塞阀中的优化算法的分析结果。从仿真曲线可以得出该锥形和圆柱形的组合缓冲方式可有效地降低活塞运动末速度、减小缓冲过程中的压力峰值,具有良好的缓冲效果。遗传算法在液压缸缓冲优化中得到良好的运用,对工程实例有普遍性,具有良好的推广价值。 参考文献: [1]丁凡.高速液压缸缓冲过程的研究[J].钢铁,1998,(8):54-57. [2] 李纪仁.油缸的缓冲装置[J].机械技术,1984,(3):21-23. [3]盛敬超.液压流体力学[M].北京:机械工业出版社,1980. [4]尹泽明,丁春利.精通MATLAB 6[M]. 北京:清华大学出版社,2002. [5] 陈永春.MATLAB M语言高级编程[M]. 北京:清华大学出版社,2004. [6]王崇骏,于汶滌,等.一种基于遗传算法的BP神经网络算法及其应用[J].南京大学学报,2003,(9):459-466. [7]Z Michalewicz. A Modified Genetic Alorithm for Optimal Control Problems [J].Computers Math Application,1992,23(12):83-94. [8]Wang Ling,Fang Chen. A Hybrid Stimation of Distribution Algorithm for Solving the Resource-constraied Project Scheduling Problem[J]. Expert Systems with Applications,2012,(39):2451-2460. [9]应瑛,寿涌毅,李敏.资源受限多项目调度的混合遗传算法[J].浙江大学学报(工学版),2009,43(1):23-27.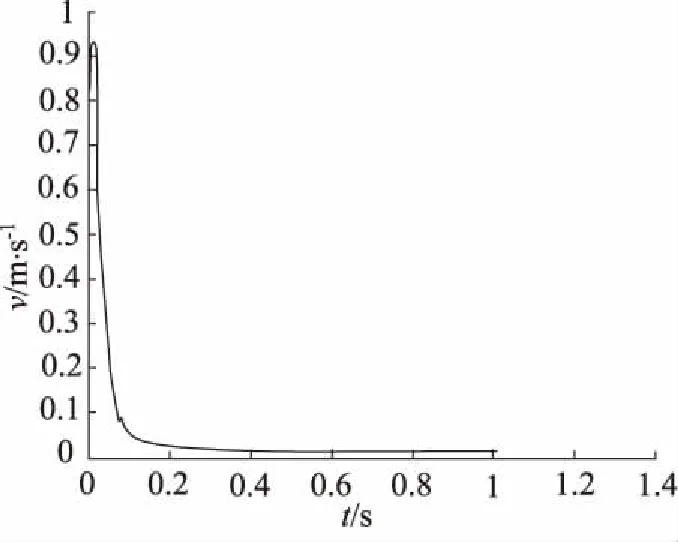

4 结论
