轧机液压伺服系统可靠性最优化与冗余技术

， 　， 　， (.武汉科技大学 机械自动化学院， 湖北 武汉　43008; .武钢大学 计算机学院， 湖北 武汉　43008)

1　液压系统可靠性最优化的原则

系统可靠性最优化主要是研究系统结构参数最优化，即研究系统可靠度、费用、重量、体积以及频率响应的最优配置[1]，应遵循以下几条原则：

(1) 确保人身安全的液压系统，应首先满足可靠度高要求的原则；

(2) 成本已确定，应尽可能优化系统配置提高可靠度的原则[2]；

(3) 工作周期长而精度要求高的液压系统，在兼顾成本的同时增加储备元件，从而提高系统可靠度；

(4) 可靠度要求不高且间断工作的液压系统，以节约投资费用为主的原则；

(5) 在满足频率响应的要求下，尽可能节约投资，方便维修的原则；

(6) 在成本允许的情况下，选用质量好和体积小的元件，降低系统复杂度和重量；

(7) 移动式的或离开地面或下沉水下的液压系统，在确保可靠度基本要求的同时，以减轻重量和减小体积为原则[3]。

2　液压系统冗余技术

2.1　冗余系统模型

在研究液压伺服系统可靠性模型中常见的可靠性模型有以下几种：

(1) 串联系统在这样的系统中，功能的实现必须依赖于系统中所有的元件都正常工作，但在每一元件中可以并联一个或多个元件备用；

(2) 并联系统在并联元件中只需要有一个部件正常工作就可以使系统正常运行。并联数越多可靠性越高，但是在实际生产中我们还必须考虑成本和重量；

(3) 混合的串-并联系统在混合系统中只需要保证有一串联系统是完好的就可以保证系统的正常运行；

(4) 混合的并-串联系统在此系统中只需要每一级并联系统中有一个元件正常工作，系统就不会失效；

(5) 旁联系统它通过故障检测和转换装置，当工作元件产生故障时，可以自动切换到另一个等待元件。在这个系统里面，元件在同一时刻并不全都投入运行；

(6)k/n系统组成系统的n个元件中如果有至少k个元件失效，则系统失效。该系统与k的取值有很大联系[4]。所以说该模型是并联系统的特例；

(7) 复杂的桥式网络系统桥式网络形式是一种复杂的可靠性系统可以提高系统可靠度。

2.2　液压系统冗余设计应考虑的几个问题

(1) 冗余度的选择从理论计算上分析，冗余度越高则系统可靠度越高，所消耗的元件费用也增加。另外还要考虑到检测及切换电路可靠性的影响，当提高冗余度时，检测及切换电路复杂度也增加，从而抵消了多重冗余的优越性。根据并联冗余有关公式计算，冗余度高，其效率并不高；

(2) 冗余级别的选择一个复杂的液压系统，可将其分成：系统、分系统、部件、元件、辅件等不同级别。根据可靠度计算公式，冗余级别越低，系统的可靠度越高，但是其容错实现上的复杂性增加，从而抵消了它的优越性。因此我们应该应用在主要机械设备上，这样既提高了可靠度又节约成本；

(3) 备份储存问题备份是动态冗余的一种最简单形式。在备份中，只需要一个系统工作，当它发生故障时，立即切换到其他备份系统继续进行工作。为了确保系统连续工作，应确保备份转换装置和故障检测器等的可靠度。

3　液压系统冗余技术最优化实例

250冷轧带钢轧机采用液压压下控制系统，为了方便研究分析，仅选取一条AGC缸控制系统作为研究对象，如图1所示。

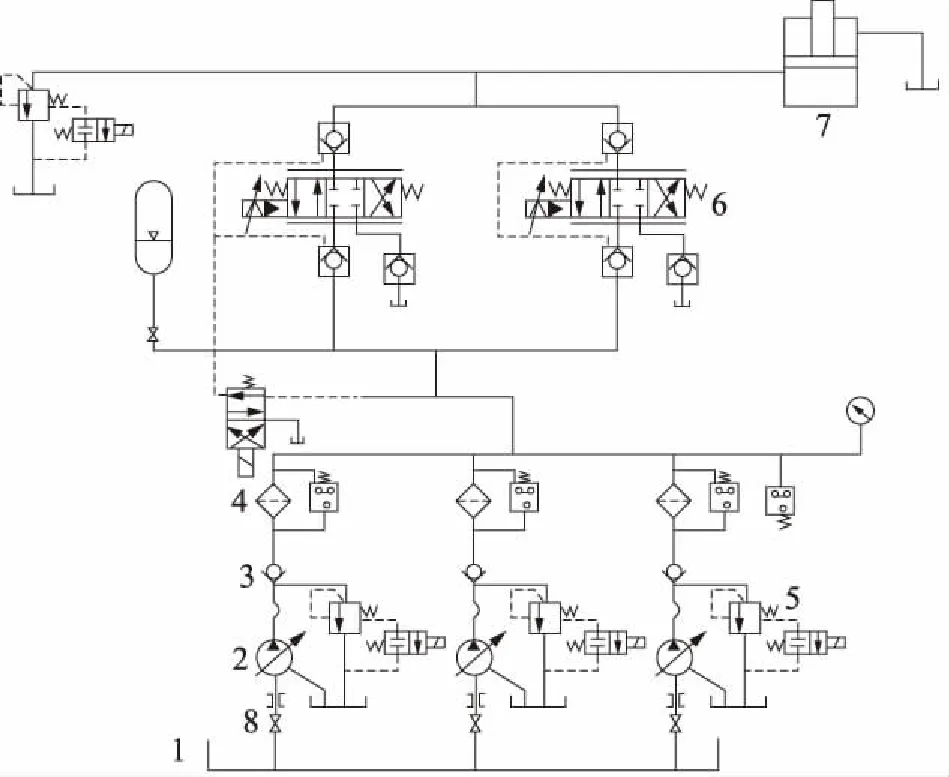
1.油箱　2.液压泵　3.单向阀　4.过滤器　5.溢流阀 6.电液伺服阀　7.液压缸　8.球阀

在此液压伺服系统中，泵的数量选取上考虑到成本问题采用2台泵组并联工作还是3台泵组并联工作，其工况是两台泵组工作，无备用泵组，3台泵组并联，其工况是两台泵组工作，1台泵组备用；在过滤器的安装选取上，考虑是安装在泵的出口还是直接安装在主油路上；在电液伺服阀数量选取上，考虑是选用1台正常工作还是配置2台伺服阀都投入工作，当某1台伺服阀失效时，另1台仍能保持正常工作。为了方便可靠性研究，将原理图简化如图2所示。

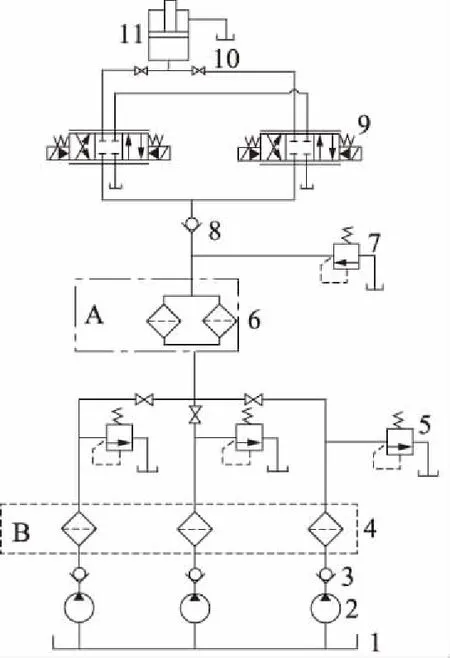
1.油箱　2.液压泵　3、8.单向阀　4、6.过滤器 5、7.溢流阀　9.电液伺服阀　10.球阀　11.液压缸

3.1　液压系统最优化建模

设计一液压系统， 根据工作条件、 性能及技术要求、投资费用、使用环境等进行优化设计[5]。首先应建立目标函数、约束条件，选择最优化的结构。

根据液压伺服系统最优化方法，初定系统中元件配置并进行优化分析计算：

(1) 在泵的选用上必须满足系统工作流量要求，因此，我们选用了2台同时供油直接工作和增加1台泵作为备用两种配置进行比较；

(2) 在过滤器选用上采用A,B两种方案进行优化比较，我们在液压油路支路上选用了3台过滤器，如图2中B和图4方案II的可靠性框图所示，另一方案在主油路上选用2台过滤器，如图2中A和图5方案III的可靠性框图所示；

(3) 在伺服阀方面，我们选用1台伺服阀工作和两台伺服阀同时工作，当1台出现故障时另1台基本上维持系统工作进行比较。

针对以上三种情况选用元件，我们根据工作条件、性能及技术要求、投资费用、使用环境进行优化配置和参数计算，建立如下两种模型。在进行最优化计算时可靠性的框图是一种重要手段，它能表示液压系统结构和工作状况。

(1) 主要元件选用2台泵、2台过滤器、1台电液伺服阀等为方案I，其可靠性框图如图3所示。

(2) 主要元件选用3台泵、3台过滤器、2台电液伺服阀等为方案II，可靠性框图如图4所示。

(3) 主要元件选用3台泵、2台过滤器、 2台电液

伺服阀等为方案III，可靠性框图如图5所示。

参考有关资料提供的数据，以及现场使用的资料，设油箱可靠度R1=0.995，泵可靠度R2=0.965，过滤器可靠度R3=0.980，溢流阀可靠度R4=0.984，球阀可靠度R5=0.972，伺服阀可靠度R6=0.975，液压缸可靠度R7=0.992，单向阀可靠度R8=0.978[1]。

3.2　液压系统最优化求解

根据上述模型，以及可靠度为目标函数，以成本和重量为约束条件进行计算，选择最优的配置方案。

(1) 在方案I如图3所示，泵组中只有2台泵工作，它分别与溢流阀、单向阀是串联的，其串联整体可靠度RS1为：

RS1=R2×R8×R3×R4×R5=0.8846

在方案II如图4所示，泵站中由3台泵组(即回路)组成，其中两个回路工作，一个回路备用，即可视为两个并联冗余，其冗余结构可靠度RS2为：

RS2=1-(1-RS1)2=0.9867

这种冗余结构可以提高可靠度：

ΔRS=RS2-RS1=0.102

这两种模型相比，泵组构成冗余结构可使可靠度可提高10.2%，为提高系统可靠度打下基础。

(2) 在过滤器的选用上，如方案II如图4所示，在各支路上分别与其他液压元件串联3个过滤器，而得到除去油箱和伺服阀以及液压缸元件外的冗余结构的可靠度RS2为：

图3　方案I

图4　方案II

图5　方案III

而如方案III如图5所示，在过滤器的选用上，我们还可以将过滤器安装在主油路上进行过滤，如图1中A所示，我们在主油路上选用2台过滤器，其除去油箱、伺服阀和液压缸液压元件外系统可靠度RS3为：

RS3=[1-(1-R2×R8×R4×R5)2]×

[1-(1-R3)2]=0.9901

由此可见过滤器安装在主油路上比安装在泵出口处分别装1台泵过滤器时可靠度提高：

ΔRS=RS3-RS2=0.0034

这两种模型相比，可靠度可提高0.34%，为提高系统可靠度打下基础。

(3) 在伺服阀的配置上，如方案I如图3所示，我用1台伺服阀单独工作其可靠度为：

R6=0.975

由此可得可靠度提高：

这两种模型相比，若选用2只同时工作，当1台出现故障后另1台仍可以维持系统工作，可靠度可提高2.4%，为提高系统可靠度打下基础。

如可靠性框图I得整个系统的可靠度RS4为：

由此可见该系统的可靠度是极低的。

根据方案III如图4，我们得到在选用3台泵构成泵组、2台过滤器构成并联结构、2台电液伺服阀构成储备系统时的可靠性RS5为：

RS5=R1×[1-(1-R2×R8×R4×R5)2]×

我们可以看出整个轧机液压伺服系统与之前相比可靠性调高不少，但提高可靠度后，投资费用也增加，这种结构应考虑业主是否能接受，如果费用偏高，可以采用低单价元件，或采用两套大流量回路并联，一套工作，一套备用。这些均要进行优化设计，从中选取最优结构。根据使用方要求。

3.3　应用MATLAB软件编程选择最优液压伺服系统

系统可靠度不能低于0.97，投资费用15万元以内,主要部件更换时间越短越好，原则上不能超过30 h。

设目标函数：

约束条件：

根据冗余技术对该系统进行最优化并建立新的方案IV如图6所示。

根据元件价格和维修时间列表如表1所示。

根据方案IV图6，设主要元件采购X个液压泵，Y个过滤器，Z个电液伺服阀。

得目标函数：

RS=R1×[1-(1-R2×R8×R4×R5)(x-1)]×

[1-(1-R3)y]×[1-(1-R6)z]×R7

约束条件为：

g=x+0.3y+3.2z+4≤15

图6　方案IV

表1　元件价格和维修时间

表2　软件编程计算的可行性结果

表3　最优配置方案

为确定更好的配置参数，通过MATLAB软件编程[6]运行得到以下结果，如表2所示。

在满足成本和可靠度的要求下，我们要保证其拆卸维修时间适中，这样可以提高工作效率，并设其拆卸时间为T：

T=4x+4y+2z≤30

我们得到以下三种组合方案供参考，如表3所示。

在实际生产中，如图1中250冷轧轧机，其辊缝调整液压伺服系统的元件配置是采用了表3中c的组合方案，其伺服阀两台并联同时工作，当1台出现故障时，另1台仍能正常维持轧制。此时迅速更换有故障的伺服阀，更换完毕后，2台伺服阀仍并联同时工作，这种冗余结构，使系统可靠度高，又节约投资。这说明我们开发的最优化方案是可行的，且在实际工作中得到广泛应用。

4　结论

如上述分析计算，我们可以看出，a,b,c三组方案无论在可靠度上还是成本上，或者是在更换时间上，都满足厂家要求。

但我们可以看出c组是可靠性最高，成本利用充分，更换时间合理的最优选择，a组为试验组中的第二方案经过MATLAB验算得到在成本上最低，更换时间上最短，也确实满足厂家条件，可靠度相比较于b,c最低，但在厂家可靠性范围以内，而b组成本，可靠性，更换时间也合理，厂家可以根据实际需求自行选择。

根据该冗余结构可知，我们并联的元件越多相应的可靠度就会提高，但是通过MATLAB计算我们知道当达到一定值时，其可靠度的增加程度很小，反而加大了成本和更换维修时间。因此我们要建立合理的模型通过计算得到最合理的配置方式。分析优化结构时，三泵组并联，三台泵中任一泵为备用，供油量和压力基本满足轧钢系统要求。这样，系统可靠度比二台泵并联，一泵工作一泵备用可靠度高。过滤器放在主油路上进行过滤不仅可靠性不减小而且降低成本，最后电液伺服阀选用两台能有效提高系统的可靠性，而且没有增加更换时间，在厂家的接受范围以内，所以设计液压伺服系统时，除了满足功能要求外，还应考虑可靠性和成本以及更换时间，否则，该液压伺服系统并不是一个优化的液压伺服系统。

参考文献：

[1]湛从昌，傅连东，陈新元. 液压可靠性与故障诊断(第2版)[M].北京：冶金工业出版社，2009.

[2]蒋仁言,左明键.可靠性模型与应用[ M] .北京:机械工业出版,2004.

[3]成大先. 机械设计手册(单行本)液压控制[ M]. 北京：化学工业出版社,2010.

[4]许耀铭.液压可靠性工程基础[M].哈尔滨：哈尔滨工业大学出版社，1991.

[5]Ansell J,Phillips M J.Practical Methods for Reliability Data Analysis[M].New York:Oxford University Press Inc.,1994.

[6]王建卫，曲中水,等.MATLAB 7.X程序设计[M].北京：中国水利水电出版社,2005.