一种新型恒功率柱塞泵斜盘角度自调节机构受力模型研究
2015-04-16烟台艾迪液压科技有限公司山东烟台265503烟台大学机电汽车工程学院山东烟台264005烟台大学山东省高校先进制造及控制技术重点实验室山东烟台264005
, , , (. 烟台艾迪液压科技有限公司, 山东 烟台 265503; 2.烟台大学 机电汽车工程学院, 山东 烟台 264005;3.烟台大学 山东省高校先进制造及控制技术重点实验室, 山东 烟台 264005)
引言
斜盘式轴向柱塞泵己广泛作为注塑机、压力机、机床、航空、工程机械和建筑机械的液压系统动力源[1-3]。在变量柱塞泵中均设有专门的变量机构,用来改变斜盘倾角的大小以调节泵的排量[4-6]。目前,变量机构通常有手动变量、压力补偿变量、恒流变量、电液比例变量、伺服变量等多种变量形式,其中,用伺服阀来调节斜盘角度的泵使用量很大,但成本较高[7,8]。给出了一种新型斜盘角度调节机构,该泵不需要伺服阀即可根据负载大小实时调节斜盘角度以控制流量,近似恒功率泵。通过对该柱塞泵流量调节机理的分析,建立了斜盘角度自适应动态调节数学模型,并进行了仿真分析和实验验证,为该柱塞泵的推广使用奠定了理论基础。
1 柱塞泵流量自适应调节机构
该新型柱塞泵流量自适应动态调节机构由斜盘2、双弹簧3、阻尼器1等组成,斜盘调节角度范围为γmax~γmin,如图1所示。当负载较小时,弹簧力推动斜盘至最大角度位置,此时泵排量最大,执行机构运动速度最快;当负载逐渐增大,处于压油区柱塞实时对斜盘产生一合力矩与弹簧力矩相抗衡,直至达到力矩平衡点,斜盘趋于平稳,由于工程机械大多负载频繁变化,斜盘角度在调节过程中会引起振荡,因此,设置阻尼器1以使系统尽快趋于稳定;负载继续增大,直至斜盘角度达到最小值,此时负载最大,而泵排量最小。

1.阻尼器 2.斜盘 3.双弹簧 4.球铰支点 5.吸油区 6.柱塞 7.压油区
2 实时调节机构数学模型的建立
为了推导斜盘角度动态调节机构受力模型,建立了如图2所示简化物理模型。
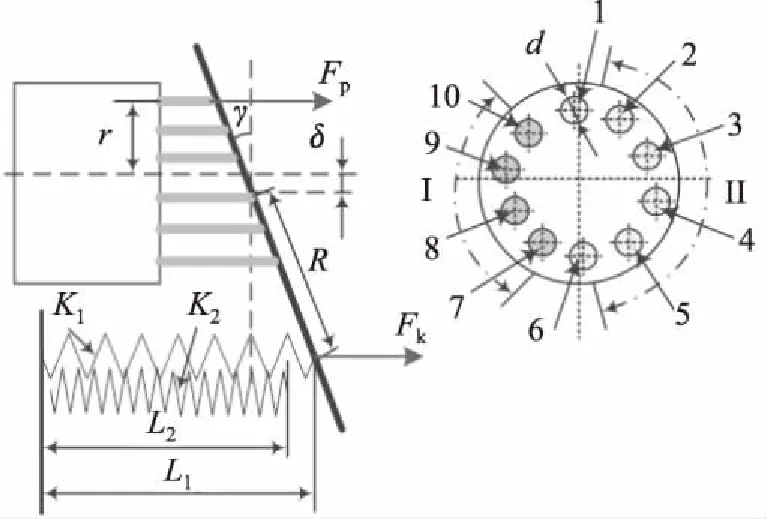
图2 柱塞泵斜盘角度调节机构简化物理模型
设柱塞泵缸体旋转中心轴线与斜盘旋转球铰支点之间偏移量为δ,斜盘倾斜角度为γ,柱塞中心分布圆半径为r,柱塞直径为d,弹簧弹性系数分别为K1、K2,Ⅰ为吸油区,Ⅱ为压油区。如图2所示,柱塞7~10处在吸油区,其压力低于0.1 MPa,而柱塞6介于吸油区和压油区之间,处于缸体底部其压力也较小,为了计算方便,这5个柱塞作用在斜盘上的作用力忽略不计。由于斜盘有倾角且缸体不断旋转,柱塞1~5逐渐把液压油压入压油区,其压力可近似为系统工作压力(压油区压力),在缸体旋转过程中柱塞2、3与柱塞4、5基本保持对称,力矩T2、T3与T4、T5相互抵消,其作用在斜盘上合力矩仅与柱塞泵缸体旋转中心轴线与斜盘旋转球铰支点之间偏移量δ有关。因此,柱塞1~5所产生的合力矩(与系统工作压力p,即负载有关)与弹簧力Fk所产生的力矩Tk共同作用来实时调整斜盘角度,进而实现了柱塞泵排量的调节。
2.1 柱塞作用在斜盘上的力矩分析
柱塞作用在斜盘上的力Fp为:
(1)
其中:
F1=pA
(2)
式中,p—— 泵输出压力或工作压力,MPa
F1—— 柱塞1作用在斜盘上的力,N
A—— 柱塞横截面积,mm2,其值为:
式中,d—— 柱塞直径,mm
故柱塞作用在斜盘上的力矩Tp为:
Tp=F1r+F2(r+δ)+F3(r+δ)-
F4(r-δ)-F5(r-δ)
(3)
式中,δ—— 柱塞泵缸体旋转中心轴线与斜盘旋转球铰支点之间偏移量,mm
F1~F5—— 分别为1~5号柱塞所产生的作用于斜盘的力,与F1近似相等,N
2.2 弹簧作用在斜盘上的力矩分析
如图2所示,为了近似逼近恒功率柱塞泵理论压力-流量特性曲线,当斜盘角度从最大值γmax变化至临界值γcr时,仅有弹簧K1起作用;当斜盘角度从临界值γcr变化至最小值γmin时,弹簧K1和弹簧K2同时起作用。
当斜盘倾角γ=γmax~γcr时,弹簧K1作用在斜盘上的力矩Tk1为:
(4)
其中,
(5)
式中,Fk1—— 弹簧K1作用在斜盘上的力,N
K1—— 弹簧K1弹性系数,N/mm
ΔL—— 弹簧K1初始压缩量,mm
γmax—— 斜盘最大倾斜角,°
γ—— 斜盘倾角,°
R—— 弹簧与斜盘连接点至斜盘球铰支点间距离,mm
当斜盘倾角γ=γcr~γmin时,弹簧K1和弹簧K2共同作用在斜盘上的力矩Tk12为:
(6)
其中,
(7)
式中,Fk12—— 弹簧K1和弹簧K2共同作用在斜盘上的力,N
K2—— 弹簧K2弹性系数,N/mm
γcr—— 当弹簧K2作用时斜盘倾角,°
γmin—— 斜盘最小倾斜角度,°
2.3 斜盘角度实时调节机构数学模型
当斜盘倾角γ=γmax~γcr,柱塞泵斜盘受力平衡时,联立公式(1)~ (5),可得压力p与斜盘倾角γ之间的数学函数关系式为:
(8)
当斜盘倾角γ=γcr~γmin,柱塞泵斜盘受力平衡时,联立公式(1)~ (3)、(6)、(7),可得压力p与斜盘倾角γ之间的数学函数关系式为:
(9)
2.4 柱塞泵流量与斜盘倾角间关系式的推导
如图2所示,缸体转一转时,泵的排量V为:
(10)
柱塞泵理论输出流量q与斜盘倾角γ之间关系式为:
(11)
式中,q—— 柱塞泵理论输出流量,L/min
Z—— 柱塞数
n—— 泵转速,r/min
r—— 柱塞中心分布圆半径,dm
3 仿真和实验分析
为验证所建立模型,针对某型号柱塞泵斜盘倾角变化范围为4°~14°,最大压力为25 MPa。由式(11)可得,柱塞泵流量随斜盘倾角变化曲线,如图3所示。随着斜盘倾角的不断增大,柱塞泵流量也逐渐增加,流量基本与斜盘倾角成正比,流量特性较好。

图3 流量随斜盘倾角变化曲线
联立公式(8)~(11)可得,柱塞泵压力-流量特性曲线,如图4所示,粗实线Ⅳ为实验曲线,细实线Ⅰ、Ⅱ、Ⅲ为仿真曲线。仿真曲线为分段曲线:当压力p较低时,不足以克服弹簧作用力时,为第Ⅰ段曲线,其流量为最大值qmax,且不随压力改变而改变,仅有少许泄漏量;当压力p逐渐升高,达到足以克服弹簧K1(如图2所示)作用力Fk1时,弹簧K1被压缩,斜盘倾角γ逐渐减小,泵流量亦逐渐减小,为第Ⅱ段曲线;随着负载进一步增加,柱塞泵输出压力也增加,此时,弹簧K2和弹簧K1同时起作用,斜盘倾角进一步减小,泵流量亦逐渐降低,当斜盘倾角达到最小时,泵输出流量也达到最小值qmin,此时为第Ⅲ段曲线。
综上,该泵压力-流量特性曲线符合恒功率柱塞泵的相关特性,实验曲线和仿真曲线基本吻合,说明所建立的数学模型是合理的。
4 结论
通过对该柱塞泵输出流量及输出压力调节机理的分析,建立了斜盘角度自适应动态调节数学模型,并进行了仿真分析和实验验证,分析结果表明,建立的大功率柱塞泵斜盘倾角动态调节模型是正确的,为该柱塞泵的进一步推广使用奠定了理论基础。
参考文献:
[1]高珊,郭勇,等.恒功率轴向柱塞泵建模及动态性能优化[J].机械设计与研究,2013,(1):83-86.
[2]陈焕明,刘卫国,等.高压大流量柱塞泵建模与仿真研究[J].机床与液压,2012,(7):139-143.
[3]刘桓龙,张燃,等.斜盘式柱塞泵结构参数对脉动特性的影响研究[J].机械制造与自动化,2012,(4):21-23.
[4]杨逢瑜,胡敏,等.斜柱塞斜盘式轴向柱塞泵柱塞的运动学及动力学特性分析[J].兰州理工大学学报,2013,37(2):52-56.
[5]高殿荣,范卓立.基于虚拟样机技术的轴向柱塞泵运动特性仿真分析[J].液压与气动,2007,(4):25-29.
[6]石金艳.液压组合阀口双三角槽尺寸对变量泵的动态特性影响研究[J].液压气动与密封,2014,(8):18-20.
[7]韩虎,等.基于MATLAB液压系统的仿真技术研究与应用[J].液压气动与密封,2007,(3):4-5.
[8]刘健.轴向柱塞泵实际流量及脉动系数的理论研究[D].杭州:浙江工业大学,2008.
