攻角对某超口径尾翼稳定弹丸气动特性的影响*
2015-04-17刘荔斌王雨时张志彪
刘荔斌,王雨时,闻 泉,张志彪
(南京理工大学机械工程学院,南京 210094)
攻角对某超口径尾翼稳定弹丸气动特性的影响*
刘荔斌,王雨时,闻 泉,张志彪
(南京理工大学机械工程学院,南京 210094)
为了研究攻角对某坦克炮超口径垂直尾翼稳定弹丸气动特性的影响,给引信弹道环境分析提供参考,应用FLUENT软件,对某大口径坦克炮超口径垂直尾翼稳定弹丸的简化模型进行三维数值模拟,得到该弹丸各气动特性参数。二次函数Cx=Cx0(1+Kα2)可用来描述弹丸阻力系数Cx随攻角α的变化,攻角系数K取值范围为13.0~16.8。在亚音速段和跨音速段,三次函数更适合用来描述升力系数Cy和俯仰力矩系数Cmz随攻角α的变化,而在超音速段,一次函数和三次函数都适合。
空气阻力特性;数值仿真;尾翼弹;弹道环境;攻角系数
0 引言
弹箭气动特性参数对于弹丸外弹道特性分析以及引信在该环境下动态特性分析必不可少。在一定的假设条件下,外弹道学文献给出非零攻角下的弹箭阻力系数为[1]:
(1)
式中:Cx0为零攻角下的阻力系数,又称零升阻力系数;Ma为马赫数;α为攻角;K为攻角系数,是常数,一般有K=15~30。
而升力系数可写为[1]:
(2)
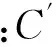
俯仰力矩系数表达式与升力系数的类似[1]:
(3)

计算流体动力学在经过多年发展后,采用大规模并行技术对弹丸外部空气流场进行数值模拟从而得到其各气动特性参数已有可行性。已有文献通过数值仿真方法系统研究了滑翔增程火箭弹、高速旋转火箭弹、单兵火箭弹、榴弹、迫击炮弹等在一定来流马赫数及攻角范围内的气动特性,为弹丸气动外形方案优选和外弹道特性分析提供参考[2-8]。
文献[9]通过数值模拟技术研究了不同攻角及不同马赫数下迫击炮弹的气动特性,并通过拟合数值仿真结果得到攻角系数K。然而通过计算流体动力学仿真软件模拟得到尾翼弹各气动特性参数,并进一步拟合其随攻角变化规律的文献至今未见。
文中以某大口径坦克炮超口径垂直尾翼稳定弹丸为研究背景,利用FLUENT仿真软件仿真得到其各气动特性参数,然后通过Matlab软件分别拟合其与攻角的函数关系。
1 计算模型
1.1 几何模型与计算域
该弹丸三维简化模型如图1,建立围绕弹丸的圆柱体流场计算域。弹丸简化模型位于计算域中部,如图2。为了消除流场计算域对仿真结果的影响,设置计算域长度为10倍弹长、直径为10倍弹径。

图1 某坦克炮超口径垂直尾翼稳定弹丸三维简化模型

图2 某坦克炮超口径垂直尾翼稳定弹丸气动特性计算域
1.2 网格划分与边界条件
为了提高计算网格划分的质量和计算精度,需对计算域进行分层处理。靠近弹丸的部分网格布置较密,远离弹丸的区域网格布置较为稀疏。对计算域采用自适应非结构化网格,并且采用二阶迎风格式,以保证较高的计算精度。全场计算域的网格单元数为436 297,分布情况如图3所示。弹丸表面网格分布情况如图4所示。取远处前方来流值作为来流初始条件,并对来流采用远场边界条件。

图3 某坦克炮超口径垂直尾翼稳定弹丸气动特性计算域网格分布
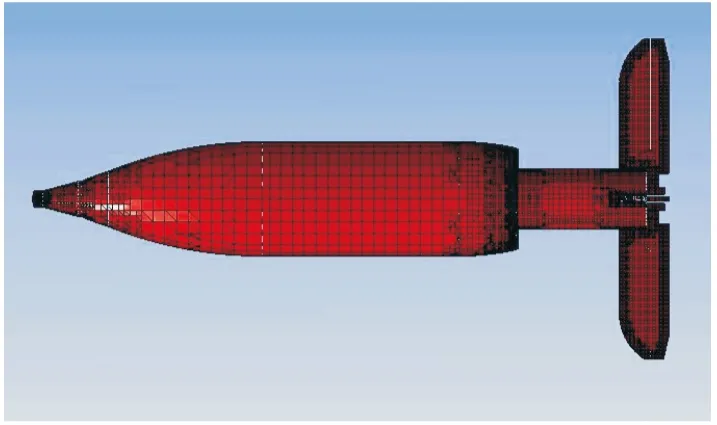
图4 某坦克炮超口径垂直尾翼稳定弹丸表面网格分布
2 仿真结果及其可信性
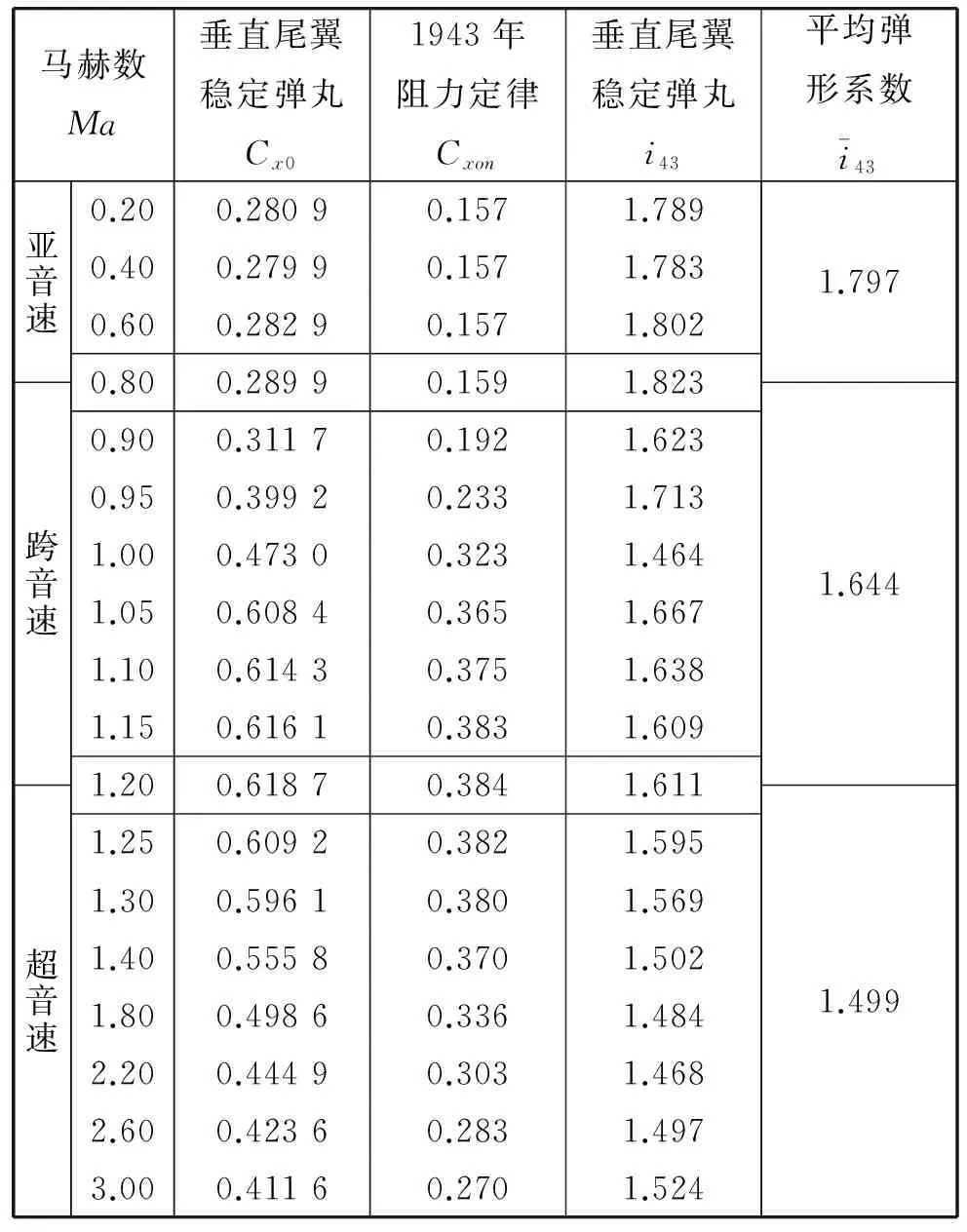
表1 某坦克炮超口径垂直尾翼稳定弹丸与标准弹的零升阻力系数及弹形系数
通过仿真得该弹丸在来流马赫数Ma=0.20、0.40、0.60、0.80、0.90、0.95、1.00、1.05、1.10、1.15、1.20、1.25、1.30、1.40、1.80、2.20、2.60和3.00,攻角α=0°时的零升阻力系数Cx0,并与标准弹的零升阻力系数Cxon(1943年阻力定律[1])计算得到该弹丸在不同马赫数下的弹形系数i43,最后计算各马赫数段的平均弹形系数,见表1。
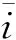
该弹丸在来流马赫数Ma=0.60、1.00、1.40、1.80、2.20、2.60、3.00,攻角α=1°、2°、4°、6°、8°、10°、12°、15°时气动特性仿真结果如图5、图6和图7。

图5 某弹丸阻力系数Cx在不同马赫数下随攻角的变化规律曲线
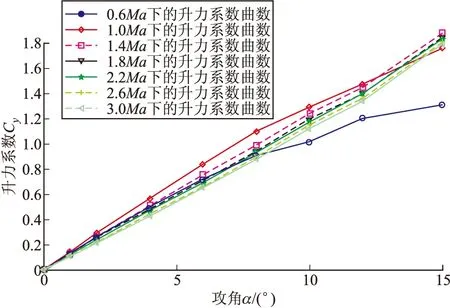
图6 某弹丸升力系数Cy在不同马赫数下随攻角的变化规律曲线

图7 某弹丸俯仰力矩系数Cmz在不同马赫数下随攻角的变化规律曲线
3 攻角对弹丸空气动力特性的影响分析
由图5可得同一马赫数下弹丸的阻力系数Cx随攻角α的增大而增大,且变化规律近似符合二次函数增大规律;由图6和图7可得同一马赫数下弹丸的升力系数Cy和俯仰力矩系数Cmz也随攻角α的增大而增大,且在亚音速段,Cy-α曲线和Cmz-α曲线稍向下弯曲,在超音速段,Cy-α曲线和Cmz-α曲线稍向上弯曲。
利用Matlab软件进行拟合。假设在同一马赫数下,弹丸阻力系数Cx随攻角α变化分别符合一次函数y=ax+b及二次函数y=cx2+dx+e和y=fx2+g;弹丸升力系数Cy和俯仰力矩系数Cmz随攻角α变化分别符合一次函数y=hx及三次函数y=lx3+nx(a、b、c、d、e、f、g、h、l、n以及其后的p、q、r均为常数),经拟合得该弹丸在不同马赫数下各空气动力特性参数随攻角α在15°以内变化时的函数见表2和表3。其中拟合系数的选取以平均相对误差最小为原则。
将弹丸的攻角数据分别代入表2和表3的曲线函数中得不同攻角及不同马赫数下各气动特性参数的拟合值,并将拟合值与仿真值对比得其相对误差结果见表4和表5。
由表4可看出,弹丸阻力系数Cx随攻角α变化更符合二次函数变化规律,且二次函数形式为y=cx2+dx+e和y=fx2+g,所得误差相差不大,y=cx2+dx+e形式所得平均相对误差最小,但y=fx2+g形式更简明,且与y=cx2+dx+e相差在1.4%以内。弹丸的攻角系数K取值范围为13.0~16.8。
由表5可看出,在亚音速段和跨音速段,弹丸升力系数Cy和俯仰力矩系数Cmz随攻角α变化更符合三次函数变化规律,一次函数形式误差较大,升力系数Cy和俯仰力矩系数Cmz中一次函数形式与三次函数形式分别相差在9.8%以内和15.8%以内,而在超音速段,一次函数形式与三次函数形式所得误差相差不大,升力系数Cy和俯仰力矩系数Cmz中一次函数形式与三次函数形式分别相差在3.1%以内和3.0%以内。因此,一次函数与三次函数形式均可近似描述弹

表2 某弹丸在不同马赫数下阻力系数Cx随攻角α变化函数

表3 某弹丸在不同马赫数下升力系数Cy及俯仰力矩系数Cmz随攻角α变化函数
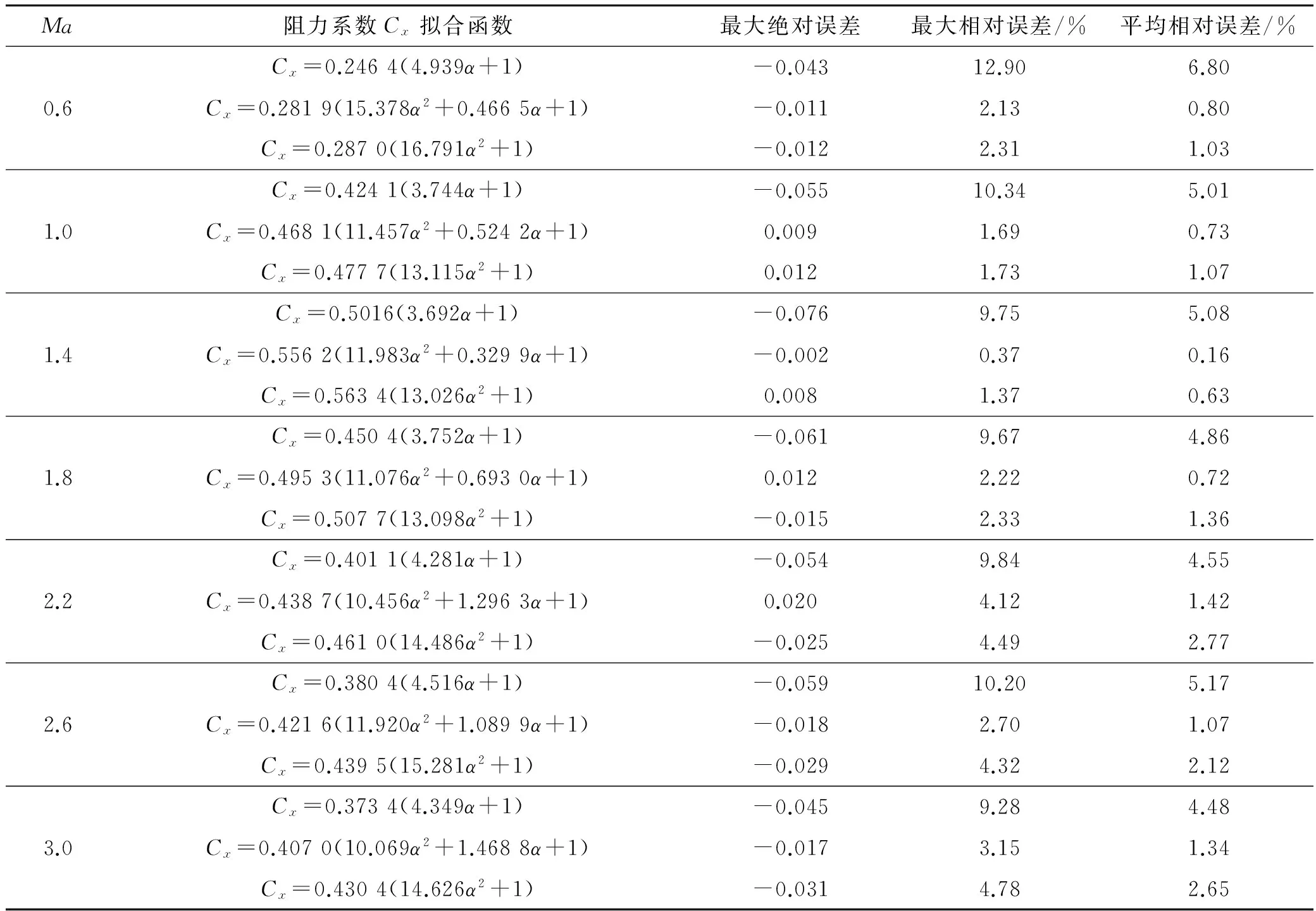
表4 某弹丸在不同攻角及不同马赫数下阻力系数Cx预测式误差

表5 某弹丸在不同攻角及不同马赫数下升力系数Cy及俯仰力矩系数Cmz预测式误差
丸升力系数Cy和俯仰力矩系数Cmz随攻角α变化规律。
4 结束语
文中通过对某大口径坦克炮超口径垂直尾翼稳定弹丸进行数值模拟,在验证模型的可信性后,对来流马赫数Ma=0.60、1.00、1.40、1.80、2.20、2.60、3.00,攻角α=1°、2°、4°、6°、8°、10°、12°、15°下弹丸气动特性进行研究,并利用Matlab软件对其阻力系数Cx按一次函数y=ax+b及二次函数y=cx2+dx+e和y=fx2+g拟合,且对其升力系数Cy和俯仰力矩系数Cmz按一次函数y=hx及三次函数y=lx3+nx拟合。结果表明:该弹丸阻力系数Cx随攻角α变化更符合二次函数变化规律,且二次函数y=fx2+g形式更简明,攻角系数K取值范围为13.0~16.8;在亚音速段和跨音速段,弹丸升力系数Cy和俯仰力矩系数Cmz随攻角α变化更符合三次函数变化规律,而在超音速段,一次函数与三次函数形式均可近似描述弹丸的升力系数Cy和俯仰力矩系数Cmz随攻角α变化规律。
[1] 浦发, 芮筱亭. 外弹道学 [M]. 修订本. 北京: 国防工业出版社, 1989.
[2] 冉秀忠. 滑翔增程火箭弹气动特性与发射动力学研究 [D]. 太原: 中北大学, 2005.
[3] 陈东阳, 芮筱亭, 王强林, 等. 超声速旋转火箭弹气动特性仿真和分析 [J]. 计算机辅助工程, 2013, 22(6): 64-68.
[4] 张连煜, 甘小红, 谭宗攀, 等. 单兵火箭弹气动特性的数值分析与试验研究 [J]. 弹箭与制导学报, 2012, 32(5): 124-126.
[5] 谢春雨, 龚华雄, 严蜀宇. 榴弹气动特性的数值分析与研究 [J]. 机电技术, 2013, 3: 11-15.
[6] 雷文星, 田晓丽, 吴建萍, 等. 一维弹道修正弹的气动特性与修正量研究 [J]. 弹箭与制导学报, 2012, 32(6): 131-135.
[7] 赵润祥, 陈少松, 崔龙波, 等. 迫击炮弹气动力三维数值模拟 [J]. 弹道学报, 1999, 11(2): 58-61.
[8] 王晓兵, 李菁, 廖忠全, 等. 基于FLUENT的弹丸外流场数值仿真 [J]. 计算机辅助工程, 2010, 19(1): 92-94.
[9] 杨翔, 王雨时, 闻泉. 迫击炮弹空气动力特性攻角系数数值研究 [J]. 弹箭与制导学报, 2014, 34(2): 139-141.
Influence of Attack Angle on Aerodynamic Characteristics of a Supper Caliber Fin Stabilized Projectile
LIU Libin,WANG Yushi,WEN Quan,ZHANG Zhibiao
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
In order to study the influence of attack angle on aerodynamic characteristics of a super caliber fin stabilized projectile of tank gun, providing refereces for analysis of ballistic condition of fuze, the aerodynamic characteristic parameters of the projectile were got by FLUENT. The analysis shows that quadratic function can be used to describe the drag coefficientCxof projectile varying with attack angle and the attack angle coefficient is 13.0~16.8. In subsonic and transonic region, the cubic function is more suitable to describe the lift coefficientCyand the pitching moment coefficientCmzof the projectile varying with attack angle. In supersonic region, linear function and cubic function are both appropriate.
air drag characteristics; simulation; fin-stabilized projectile; ballistic condition; attack angle coefficient
2014-11-05
刘荔斌(1990-),男,江苏无锡人,硕士研究生,研究方向:现代引信技术。
TJ43
A
