雷达导引头隔离度寄生回路对制导回路影响研究*

李 娜,冯 星,李 强,夏群利

(1 空间物理重点实验室,北京 100076;2 中航工业洛阳电光设备研究所,河南洛阳 471009;3 北京理工大学宇航学院,北京 100081)

雷达导引头隔离度寄生回路对制导回路影响研究*

李 娜1,冯 星2,李 强3,夏群利3

(1 空间物理重点实验室,北京 100076;2 中航工业洛阳电光设备研究所,河南洛阳 471009;3 北京理工大学宇航学院,北京 100081)

为了分析雷达导引头隔离度对制导回路的影响,提出了考虑隔离度相位滞后的寄生回路模型,利用无量纲化方法分析了不同相位滞后对隔离度寄生回路稳定性的影响,确定了正反馈比负反馈具有更小的稳定域,而最小稳定域出现在滞后为-90°～-180°之间并进一步确定了滞后超过-90°时稳定特性与正反馈情况相似。该结论在工程应用中对提高制导回路稳定性具有重要意义。

导引头;隔离度;相位滞后;寄生回路;稳定性

0 引言

现代科学技术水平的不断发展和军事、政治等方面的需求不断增加,使得远程机动飞行、快速精确打击成为新一代导弹的必然发展趋势和动向。导引头作为精确打击导弹的核心技术,能够实现对目标的自主搜索、识别与精确跟踪,为导弹提供准确的制导信息。作为制导回路的一部分,导引头性能直接影响到弹体的运动状态,同时弹体的运动也会影响导引头的跟踪性能,所以导引头和弹体是相互联系的,二者之间形成了一个闭环回路,称为导引头隔离度寄生回路,隔离度水平将直接影响导弹的制导精度。

崔莹莹[1]等在对导引头输出信号基准问题研究的基础上,建立以电机输出绝对角速度为基础的隔离度模型,并对两种隔离度模型进行了对比,指出导引头隔离度模型建立应以电机输出绝对角速度为基础。赵超[2]对影响隔离度因素进行了讨论,分析了弹体扰动作用的本质和摩擦力矩的关系,并对探测器处理延迟对隔离度的影响进行了较为全面的分析研究。考虑工程应用要求,对于隔离度的研究应该结合制导律和自动驾驶仪等特性,从制导的角度将隔离度与其它环节相结合,综合考察其对制导回路的影响。文中从总体的角度,结合制导回路开展了导引头隔离度寄生回路稳定性的研究,并提出了隔离度相位滞后的概念,同时研究了隔离度幅值和相位滞后对制导回路的影响。

1 隔离度数学模型建立

导引头是安装于动基座上的一种光电设备,在工作过程中要求导引头的指向不受基座运动的影响,在惯性空间保持指向不变。导弹在飞行过程中,由于发动机和空气阻力等因素的影响,弹体始终处于剧烈振动摇摆中,弹体与导引头之间始终存在相对角运动,这种相对运动将通过导线拉扯、轴承之间的动静摩擦等将弹体的运动耦合至导引头的运动,影响导引头在空间的指向。

隔离度是导引头的一项重要指标,显示了导引头隔离弹体扰动的能力,是评价导引头伺服系统扰动隔离性能的一个重要指标,并且直接关系到导弹的制导精度[3]。对于只考虑幅值影响的传统形式,其表达式可写为:

(1)

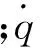
1.1 电机回路模型

随着导引头小型化及电机水平的不断提高,越来越多的导引头采用力矩电机进行驱动。根据电机转矩动态平衡、电机电压动态平衡等方程可以确定电机回路模型如图1所示。

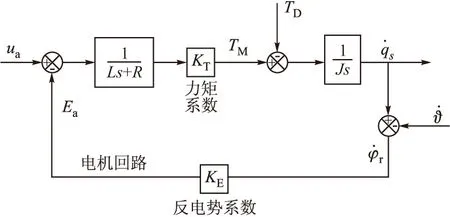
图1 力矩电机数学模型基本框图

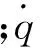
1.2 隔离度寄生回路模型

通过角速率陀螺测量相对于惯性空间的导引头和弹体的转动角速度,进一步获得导引头相对于弹体的转动角速度,经过反电势和干扰力矩模型得到相应的反电势和干扰力矩,得到隔离度寄生回路如图2所示[4]。

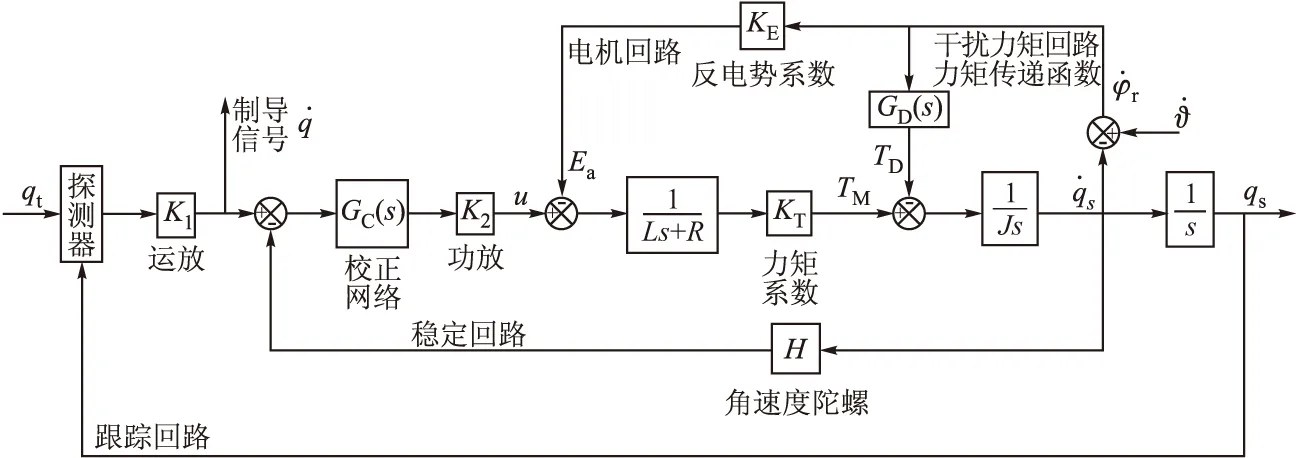
图2 隔离度寄生回路模型

(2)

当弹目视线角qt=0时,弹体扰动引起的导引头平台转动角速度稳态值为:

(3)

弹体扰动引起的视线角速度有两部分,一部分是由于干扰力矩引起的,另一部分是由于电机的反电势引起的。通常情况下电机反电势系数KE与稳定回路的功放K2和稳定回路校正网路GC(s)增益相比很小,因此反电势引起的隔离度较小;力矩电机一旦确定则电阻R和力矩系数KT就已确定,能减小干扰力矩影响的有效办法就是增大K2和GC(s)的增益。因此,减小导引头隔离度的主要方法就是提高稳定回路的增益。

2 隔离度寄生回路对制导回路影响研究

(4)

图3给出了包含导引头隔离度寄生回路的比例导引制导回路方块图[5]。

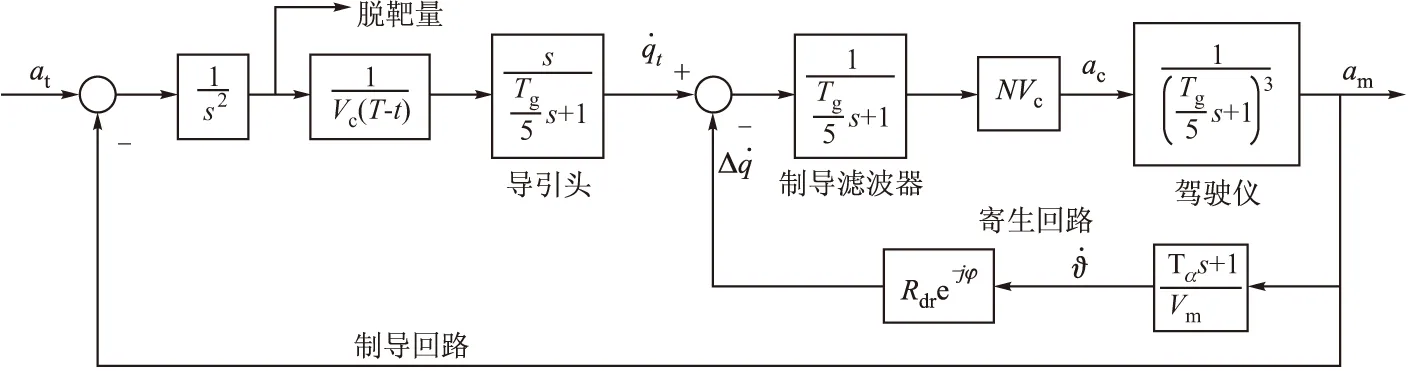
图3 包含隔离度寄生回路的制导回路

上图以五阶一次系统来表示制导系统,其中导引头一阶,制导滤波器一阶,自动驾驶仪三阶。Tg为制导系统时间常数,Tα为导弹攻角时间常数,N为比例导引系数,Vc为弹目相对运动速度,Vm为导弹飞行速度,Rdr为导引头隔离度幅值,φ为导引头隔离度的滞后角,T为导弹的末制导时间。

通过上图可知,当弹目相对距离较远,即Vc(T-t)较大时,制导回路的稳定性主要由寄生回路的稳定性决定,因此寄生回路稳定性将对制导回路产生重要影响[6]。

3 隔离度寄生回路稳定性研究

为方便分析寄生回路特性,采用无量纲化方法减少参数个数[7],令:

(5)

(6)

无量纲的寄生回路模型如图4所示[8]。

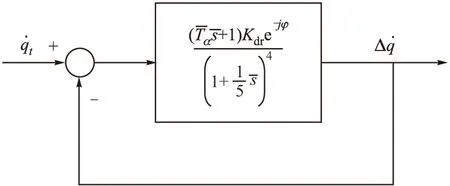
图4 无量纲化的寄生回路

得到导引头隔离度寄生回路的开环和闭环传递函数为:

(7)

(8)

其中:

3.1 不同系统反馈对寄生稳定性影响

选取极限情况,令式(8)中φ=0°和φ=-180°,则分别对应系统负反馈和正反馈的情况。根据劳斯稳定性判据,采用数值方法得到寄生回路稳定边界如下图所示。

图5 正、负反馈时寄生回路稳定边界

从图5可以看出,隔离度相位滞后为0、寄生回路为负反馈时寄生回路的稳定域比相位滞后为-180°、寄生回路为正反馈时的要大。攻角时间常数与制导系统时间常数的比值越大,则寄生回路的稳定域就越小;比例导引系数、导引头隔离度水平以及弹目相对运动速度与导弹飞行速度的比值越大,寄生回路的稳定域也就越小。

3.2 不同相位滞后对寄生稳定性影响

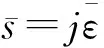
(9)

采用乃奎斯特图分析寄生回路的稳定性,得到不同相位滞后角时的临界稳定曲线如图6所示,曲线以上部分为不稳定部分,曲线以下部分为稳定部分。

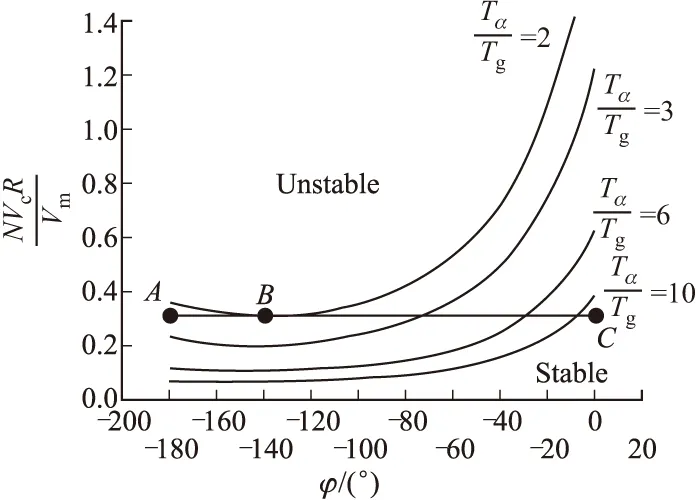
图6 不同相位滞后时寄生回路稳定边界

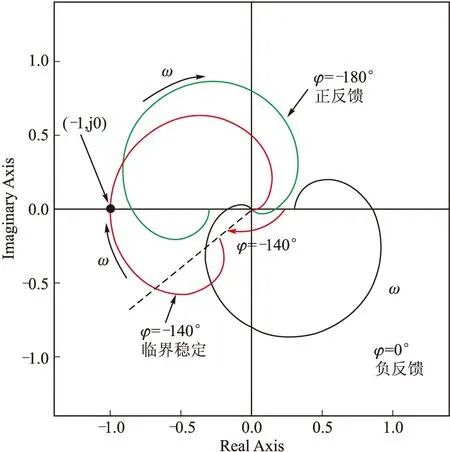
图7 不同相位滞后的Nyquist图

从上图可以看出,A点和C点乃式曲线都没有包围(-1,j0)点,所以这两种情况都是稳定的,而B点乃式曲线正好穿越了(-1,j0)点,此时系统是临界稳定的。

4 总结

文中围绕导引头隔离度这一关键指标,对隔离度的基本概念、隔离度的产生原因进行了深入的研究,建立了合理的隔离度模型。提出了考虑相位滞后的隔离度寄生回路,将隔离度寄生回路与制导回路相结合,并利用无量纲化方法开展不同相位滞后对寄生回路稳定性分析。得到如下结论:正反馈比负反馈更易失稳,但稳定域并不是最小,最小的稳定域出现在-90°～-180°之间,并且滞后超过-90°稳定特性就接近正反馈。文中的结论对提高雷达导引头制导回路稳定性具有一定工程应用价值。

[1] 崔莹莹, 夏群力, 祁载康. 导引头稳定平台隔离度模型研究 [J]. 弹箭与制导学报, 2006, 26(1): 22-25.

[2] 赵超. 导引头稳定系统隔离度研究 [J]. 电光与控制, 2008, 15(7): 96-100.

[3] Garnell P, Qi Zai-kang, Xia Qun-li. Guided weapon control system [M]. Second Revision. Beijing Institute of Technology Press, 2004: 220-245.

[4] 张宏. 增强型比例导引的理论与工程应用研究 [D]. 北京: 北京理工大学, 2007: 14-24.

[5] Waldmann J. Line-of-sight rate estimation and linearizing control of an imaging seeker in a tactical missile guided by proportional navigation [J]. IEEE Trans. on Control Systems Technology, 2002, 10(4): 556-567.

[6] 吴鹏. 精确制导光电导引头稳定平台数字控制技术 [J]. 弹箭与制导学报, 2002, 22(3): 37-41.

[7] 夏群力, 祁载康, 王磊. 闪烁输入下比例导引系统无量纲化研究 [J]. 系统仿真学报, 2007, 19(9): 2015-2017.

[8] 杜运理. 导引头状态估计及隔离度影响研究 [D]. 北京: 北京理工大学, 2011: 82-100.

The Effect of Disturbance Rejection Ratio Parasitical Loop on the Guidance Loop for Radar-Seeker

LI Na1,FENG Xing2,LI Qiang3,XIA Qunli3

(1 Key Laboratory of Space Physics, Beijing 100076, China;2 Luoyang Institute of Electro-optical Equipment, AVIC，Henan Luoyang 471009, China;3 School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

In order to analyzing the effect of disturbance rejection ratio on guidance loop for radar-seeker, parasitical loop model considering disturbance rejection ratio with phase lag was proposed. After the analysis of stable zone of parasitical loop with phase lag based on non-dimensional-normalization method, it is concluded that the stable zone of the feedfoward is smaller than feedback, the smallest stable range occurs between -180° and -90° phase lag but not -180°, and when the phase lag is over -90°, the stable zone is close to the case when the phase lag is -180°. These conclusions have great significance for improving stability of guidance loop in engineering applications.

seeker; disturbance rejection ratio; phase lag; parasitical loop; stability

2014-09-02

李娜(1983-),女,陕西宝鸡人,工程师,硕士,研究方向:导航与制导控制。

TJ765.3

A