基于高斯伪谱法的有控火箭弹弹道优化方法*

沈冠军,冯顺山,曹红松

(1 中北大学机电工程学院,太原 030051;2 北京理工大学爆炸科学与技术国家重点实验室,北京 100081)

基于高斯伪谱法的有控火箭弹弹道优化方法*

沈冠军1,冯顺山2,曹红松1

(1 中北大学机电工程学院,太原 030051;2 北京理工大学爆炸科学与技术国家重点实验室,北京 100081)

为了解决有控火箭弹弹道优化问题,文中提出一种基于Gauss伪谱法的弹道优化设计方法。首先在纵向飞行平面内建立火箭弹运动模型,将运动过程等效为路径约束,以飞行始末状态为边界约束条件,建立起有控火箭弹弹道优化模型。基于Gauss伪谱法将弹道优化问题转化成一系列非线性规划问题并以序列二次规划法求解。最后以某型火箭弹射程为优化指标进行仿真,经优化后在保持飞行稳定的前提下弹道射程明显增加,表明文中所提出的优化设计方法可有效地对弹道进行优化,并且具有收敛速度快的特点。

高斯伪谱法;有控火箭弹;弹道优化

0 引言

弹道优化是火箭弹弹道设计中的一个重要环节,通过对火箭弹弹道轨迹和控制规律的优化,以提高火箭弹的飞行性能。随着计算机技术和最优控制理论的发展,数值法求解最优控制问题逐渐在弹道优化中得到了普遍应用[1]。文献[2]应用极大值原理求解弹道修正引信弹道优化模型,得到了最优法向控制量。文献[3]对间接法进行弹道优化时无法获得全局最优解的缺点,提出了一种改进方法。间接法获得解的精度高,但是推导最优性条件困难、收敛半径小、协状态变量初值猜测困难。为解决间接法在弹道优化中的不足,文献[4]通过序列二次规划法求解了参数化后的助推滑翔导弹弹道优化问题,文献[5]利用Radau伪谱法将助推-滑翔飞行器弹道优化问题转换为非线性规划问题,文献[6]根据伪谱法将再入动力学微分方程约束转换成代数方程约束,将制导问题转换为不需要积分的最优规划问题。

文中结合Gauss伪谱法无需对微分方程求解,设置参数较少且精度较高的特点,建立了有控火箭弹飞行平面内弹道优化模型,基于Gauss伪谱法将最优控制问题转换为非线性规划问题,以序列二次规划法对此非线性规划问题进行求解,最终得到最优控制问题的解,并通过实例进行该方法的验证。

1 运动模型的建立

文中以一种鸭式布局的简易控制火箭弹为研究对象,其飞行过程如下:当火箭弹出炮口后一定时间,鸭舵张开进行控制,舵片的张开改变了火箭弹原来的气动布局而产生不同的气动力,不同的起控时间和舵片偏转规律将影响火箭弹飞行性能,文中将舵片偏转作用等效成飞行攻角,以等效攻角的形式在火箭弹纵向飞行平面内建立运动方程组:

(1)

式中:V为飞行速度;θ为弹道倾角;x为射程;y为弹道高;α为飞行攻角;X、Y分别为空气阻力和升力,可用式X=ρSCdV2/2,Y=ρSCyV2/2表示;S为弹体特征面积;Cd、Cy为阻力系数和升力系数,计算中可通过数据表格的形式进行插值获得;ρ为大气密度,大气模型参考文献[7]。

2 优化问题描述

由式(1)可以看出,当火箭弹过弹道顶点进入滑翔飞行阶段,速度和弹道倾角的大小是影响射程的直接因素,同时重力的分量也是不可忽略的因素。在滑翔阶段开始至结束[t0,tf]的时间段内,通过改变舵偏角大小使火箭弹产生不同的滑翔攻角α以产生足够的升力减缓弹道倾角的改变,提高火箭弹在空中的滞留时间,对提高射程具有一定的影响。优化问题可以归结为:以射程为优化性能指标,在时间段[t0,tf]内,tf终端自由,满足相关中间约束与终端约束,寻找攻角的最优控制规律,其实质是一个终端时间自由,末段受约束,控制受约束,末值型性能指标,建立优化模型如下:

1)性能指标:文中以研究火箭弹在给定射角下的最大射程,故性能指标为:

(2)

2)状态约束:为式(1)纵平面运动方程;

3)边界条件:由式(1),满足以下边界条件:

(3)

4)控制变量约束:文中以滑翔攻角为控制变量,因控制舵所能产生的滑翔攻角有限,同时滑翔攻角应该满足弹体在空中的飞行稳定性:

(4)

5)起始、终端状态

初始条件:V=v0,θ=θ0,x=x0,y=y0

终端约束:V=vtf,θ=θtf,x=xtf,y=ytf

3 优化问题求解

3.1 优化原理及流程

将弹道优化问题看作一般的最优控制问题:寻找控制变量u(t)∈Rm,最小化具有一般性的Bolza型性能指标:

多发性内分泌肿瘤-Ⅱ型是多器官(两个或两个以上)同时或者相继发生的增生或肿瘤病变,包括甲状旁腺功能亢进、甲状腺髓样癌及肾上腺髓质病变,属于染色体显性遗传疾病,有研究显示其有遗传缺陷的基因位于第l0号染色体上。文献资料提示MEN-Ⅱ型患者在甲状腺、甲状旁腺疾病出现之后,平均两年九个月时有儿茶酚胺增多病征出现。组织病理检查并不能区分肿瘤的良恶性,因此,患者应终身随访。

(5)

式中,状态变量x(t)∈Rn、初始时间t0和终端时间tf满足动力学微分方程约束:

(6)

满足式(7)边界条件和式(8)路径约束:

(7)

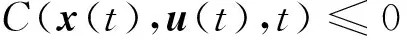
(8)

求解优化问题应对优化问题参数化,将优化问题转换成非线性规划问题,进而采用成熟的序列二次规划算法进行求解。结合上节优化模型,其求解过程如图1所示。

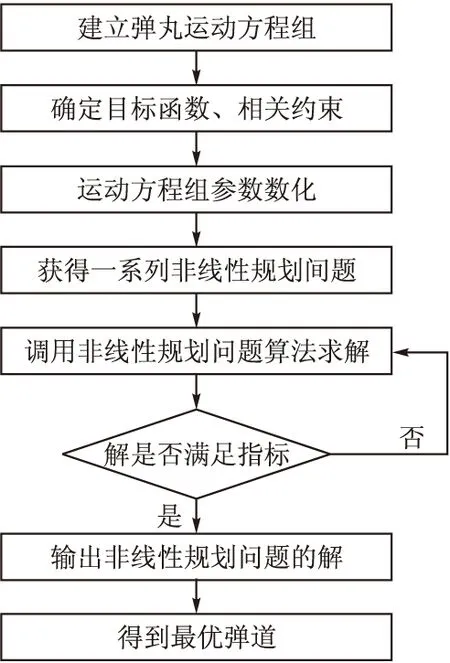
图1 弹道优化流程

3.2 优化问题参数化过程

1)将最优控制问题的时间由t∈[t0,tf]离散到τ∈[-1,1],变换如式(9)所示:

(9)

2)选取K个LG点以及τ0=-1作为离散节点,以(K+1)个Lagrange插值多项式Li(τ)(i=0,…,K)为基函数来近似状态变量的时间历程。

(10)

(11)

(12)

3)Gauss伪谱法中的节点包括配点(τi,…,τk)和初始点τ0≡-1以及终点τf≡1。式(10)未定义终端状态X(τf),终端状态应满足动力学方程约束:

(13)

将终端状态约束条件离散并用Gauss积分近似:

(14)

4)对式(10)求导可得状态变量导数,将动力学方程约束转换为代数约束:

(15)

(16)

式中：τk(k=1,…,K)为集合κ中的点,而τi(i=1,…,K)属于集合κ0={τ0,τ1,…,τK}。最优控制问题的动力学微分方程约束即转换为代数约束:

(17)

5)将Bolza型性能指标函数中的积分项用Gauss积分来近似,得到在Gauss伪谱法中的近似性能指标函数:

(18)

综上5个步骤,Gauss伪谱法将连续最优控制问题离散并转换成为非线性规划问题,详细的步骤参考文献[8-9]。

4 仿真实例

以某小型火箭弹为例,将火箭发动机主动段末速度等效为炮口速度,弹体质量m0=14.5 kg,出炮口速度v0=650 m/s,起始射角θ0=45°,气动数据通过气动软件计算获得,飞行最大允许攻角|α|≤20°,未经优化前在此发射条件下射程为13.14 km,优化后应使火箭弹射程x≥20 km,落角θ≥40°,落点速度V≥200 m/s,终端时间自由。

利用上述伪谱法原理,将方程组进行参数化,编制程序,选取插值点数分别为20、30、50,在计算机内存为8 G,主频为2.66 GHz四核环境下,其耗时如表1所示。

由表1数据得出,优化计算耗时随着插值点数的增加而增加。插值点数较多,时间间隔较小,描述控制量的变化情况越细致,能够避免在插值点数较小下描述问题的不精确性,但是插值点数越多计算耗时越多,故需要合理设置插值点数满足一定的精度下所需时间最少。

图2和图3分别为插值点数为20、30、50的射高曲线和攻角曲线。由图2中可以看出,在插值点数为30和50下优化后的射高曲线基本一致,而在插值点数为20下射高曲线无法描述最优射高曲线,在20～80 s间具有明显的偏差。由图3中攻角曲线可以看出,在时间20～40 s,随着点数增加攻角逐步向最优值逼近。

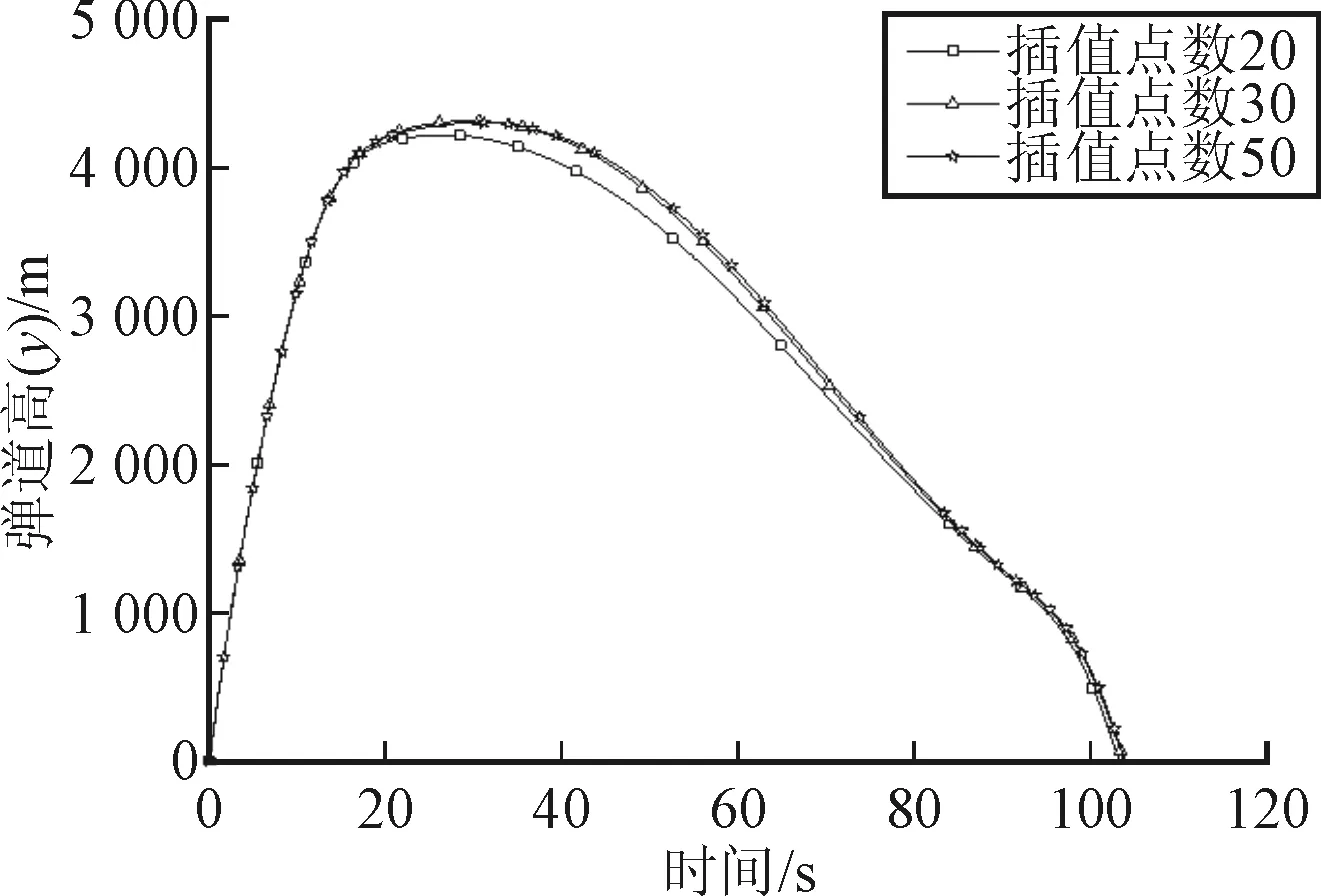
图2 不同插值点数下的射高曲线

图3 不同插值点数下的攻角曲线

图4 插值点数为30的哈密顿函数

综合上述,文中选取插值点数为30,图4是该优化问题的哈密顿函数曲线,由庞特里亚金极小值定理可知,末端时间自由的优化问题其哈密顿函数为零。图4中曲线量级在10-13证明了此优化问题解的最优性。

表2为优化前后的弹道参数对比,由表2可知,优化后的弹道最大射程为23 km,落点速度229.84 m/s,落角55°,满足落点约束条件。

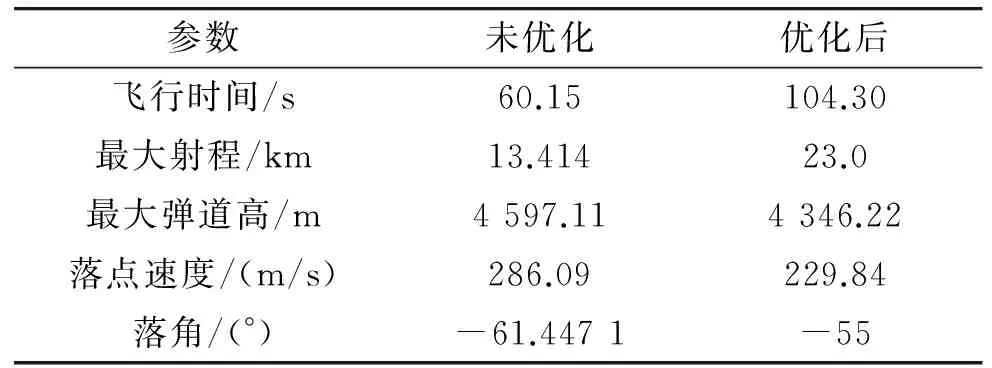
表2 优化前后弹道参数对比

图5～图9为通过高斯伪谱法得到的弹道参数和未优化前的弹道参数对比曲线。由图5射程对比曲线可知,弹道经优化后射程明显增加。由图6、图7可知,优化后的弹道在弹道顶点处相比原弹道相对平缓,产生这一现象在于弹道初始段,弹体以一定正攻角飞行产生升力来减缓弹道倾角的改变。当火箭弹接近弹道顶点处,控制机构改变飞行攻角,在负攻角的作用下弹道被拉平。过弹道顶点后,火箭弹在控制机构作用下按正攻角飞行以抵消重力分量,达到提高射程的目的。

图5 优化前后射程对比

图6 优化前后射高对比

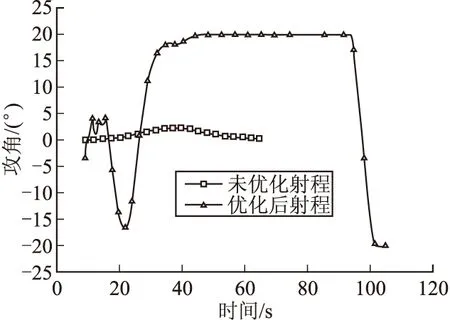
图7 优化前后攻角对比

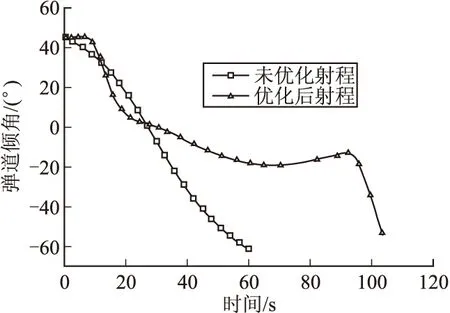
图8 优化前后弹道倾角对比

由图8所示弹道倾角变化曲线可知,在图7优化后的攻角控制律下,弹道倾角相对未优化前变化较缓慢,尤其是在弹体过弹道顶点后,优化后的弹道倾角变化率明显小于未优化前,这也从另一方面解释了图6中射高相比未优化前平直。弹体在正攻角不断作用下产生向上的升力抵消重力分量从而使图9中过弹道顶点速度基本维持在一定值。

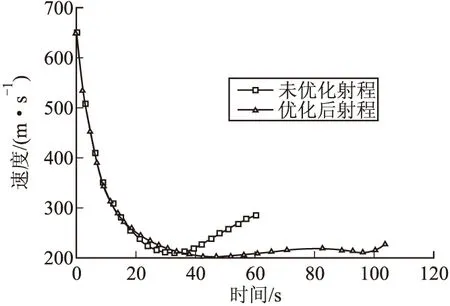
图9 优化前后速度对比

在弹道末段,随着攻角的减小弹体产生的升力减小,引起速度和弹道倾角变化率的增大,如图8中末段弹道倾角变化现象所示。弹体在过弹道顶点后以较小的弹道倾角进行飞行以提高射程,但是较小的落角使得弹体在终点产生跳弹等现象,减小弹体的终点毁伤效能,那么针对有落角约束的弹道在弹体离地一定距离时,设置合理的控制规律以增加弹道倾角的改变以满足落角约束的要求,从图中可以看出,在此攻角的控制规律作用下,弹道倾角的变化规律是满足上述要求的。

综合上述分析并且结合弹箭飞行知识可以得出,通过高斯伪谱法优化得到的弹道参数是合理的。

5 结论

文中基于高斯伪谱法对常规有控火箭弹弹道进行了优化分析,仿真结果表明,相比间接法该方法能够快速对控制变量进行求解,并且所求解满足最优控制理论中最优解的必要条件;通过合理的选取Gauss插值点数和建立适当的弹道优化模型,Gauss伪谱法的求解精度和速度能够为火箭弹简易制导中最优制导律设计提供参考;同时利用高斯伪谱法对弹道进行优化是一种全局搜索方法,很好的避免了火箭弹飞行过程中模型参数不确定性的干扰,具有很好的鲁棒性。

[1] 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述 [J]. 宇航学报, 2008, 29(2): 398-404.

[2] 霍鹏飞, 施坤林, 苑伟政. 基于极大值原理的弹道修正引信弹道优化控制研究 [J]. 兵工学报, 2007, 27(3): 301-304.

[3] 李永远, 姜毅, 高伟涛, 等. 间接法求解具有最大横程的再入轨迹 [J]. 北京理工大学学报, 2013, 33(7): 665-668.

[4] 李瑜, 杨志红, 崔乃刚. 助推-滑翔导弹弹道优化研究 [J]. 宇航学报, 2008, 29(1): 66-70.

[5] 李柯, 聂万胜, 冯必鸣. 助推-滑翔飞行器规避能力研究 [J]. 飞行力学, 2013, 31(2): 148-156.

[6] 水尊师, 周军, 葛致磊. 基于高斯伪谱方法的再入飞行器预测校正制导方法研究 [J]. 宇航学报, 2011, 32(6): 1249-1254.

[7] 林献武. 高空环境下弹箭的弹道特性研究 [D]. 南京: 南京理工大学, 2009.

[8] Garg Divya, Hager W W, Rao A V. Pseudospectral methods for solving infinite-horizon optimal control problems [J]. Automatica, 2011, 47(4): 829-837.

[9] Maleki Mohammad, Hashim Ishak. Adaptive pseudospectral methods for solving constrained linear and nonlinear time-delay optimal control problems [J]. Journal of the Franklin Institute, 2014, 351(2): 811-839.

Trajectory Optimization for Controllable Rockets Based on Gauss Pseudo Spectral Method

SHEN Guanjun1,FENG Shunshan2,CAO Hongsong1

(1 School of Mechatronics Engineering, North University of China, Taiyuan 030051, China;2 State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

To solve trajectory optimization problems of controllable rockets, an optimization design method based on Gauss pseudo spectral method was proposed. The motion model of rockets in flight plane was established, the movement of rockets was taken as path constraints, and then the conditions of flight start and end point were taken as boundary constraints, trajectory optimization model was established. This trajectory optimization problem was transformed into a series of nonlinear programming problems based on the Gauss pseudo spectral method and solved by sequential quadratic programming method. Finally, with range as the optimization index, a certain type of rocket was simulated, the trajectory range significantly increased after optimization while the stability of the flight was maintained, which shows the proposed optimization method can effectively optimize trajectory and has a characteristic of fast convergence speed.

Gauss pseudo spectral method; controllable rockets; trajectory optimization

2014-07-17

兵科院支撑基金(62201070503)资助

沈冠军(1987-),男,浙江长兴人,博士研究生,研究方向:弹道优化技术。

TJ013.2

A