BTT弹体耦合特性分析*

张 頔

(北京机电工程研究所,北京 100074)

BTT弹体耦合特性分析*

张 頔

(北京机电工程研究所,北京 100074)

基于倾斜转弯导弹的运动学和动力学特性,建立倾斜转弯导弹的弹体模型,根据弹体耦合特点进行解耦分析。针对不同耦合特点,分析了运动学耦合、气动耦合和控制学交叉耦合产生原因,通过仿真阐明了各项耦合对控制系统设计产生的影响。基于BTT快速消侧滑的特点,需重点分析对侧向影响较大的耦合项。研究表明在控制系统设计时应关注运动学耦合和控制学交叉耦合对设计性能的影响,为以后的控制系统设计提供便利。

倾斜转弯导弹;运动学耦合;气动耦合;控制学交叉耦合

0 引言

BTT控制技术因其对“面对称”飞行器机动性的良好发挥及与先进的冲压发动机进气口设计的兼容性等[1]特点引起控制系统工程师的广泛关注。远程防区外面对称空地导弹、配备冲压发动机的超远程空空弹的中导段和小型面对称空地制导武器[2]三个领域是BTT控制技术应用的重点方向。此类飞行器都具有面对称气动外形,有有效提高气动效率,降低被雷达探测的可能性,大幅提高飞行速度和射程。但由于控制模式的需求,飞行器需在受控过程中进行快速旋转,使得三通道耦合强烈,在建模时不可做简单忽略,这使得控制系统的设计更加困难。因此对BTT飞行器而言,对耦合特性的分析是十分必要的。

公开文献表明,工程上对耦合项的处理有以下方法:Arrow等[3]忽略交叉耦合,单独设计每个通道,后加入协调支路抵消耦合作用;Emmert等[4]将耦合视为干扰设计了三通道独立的控制器。古典控制方法在工程上易于实现,但是耦合项带来的影响需进一步分析研究。

文中着重研究BTT控制下各耦合项的产生原因及影响。利用弹体的数学模型推导运动学耦合项的稳态值,分析了气动耦合和运动学耦合对控制系统的影响,为后续的控制系统设计提供便利。

1 BTT导弹模型

根据弹体特性,基于小扰动线性化假设对导弹6个动力学方程[5-6]进行简化得到:

(1)

(2)

(3)

(4)

(5)

其中:αωx、-βωx为运动学耦合项;ωyωz(Jy-Jz)/Jx、ωxωy(Jx-Jy)/Jz为惯性耦合项;aωxωx-aδaδa、-cββ、-cωyωy-cδrδr为气动交叉耦合。

式(1)～式(5)中符号对应的物理意义及定义如下:

角度:α为攻角(°),β为侧滑角(°);δr、δa为方向舵偏角和副翼偏转角(°)。

角速度:ω*为弹体坐标系相对地面坐标系*轴转动角速度矢量(°/s);

转动惯量:J*为弹体系下关于*轴转动惯量(kg·m2)。

6个动力学方程中的动力学系数定义如下[7]:

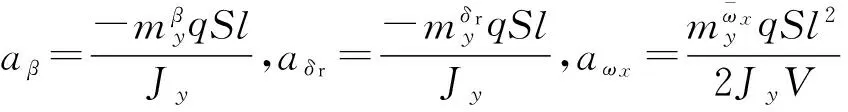
对于方程中的运动学耦合项,由于偏航通道尽力抑制β,因而-βωx很小,可忽略-βωx项,略去方程中惯性耦合项,俯仰、偏航通道解耦后得到[8]:

(6)

但偏航、滚转通道间的气动耦合项不可简单忽略,其中α和ωx变化较大,αωx不可忽略;但在巡飞段飞行的导弹常常保持一定的正攻角α0飞行,可以引入常值平衡攻角α0,作为不确定量来处理[9]。因而,BTT控制偏航、滚转通道的方程可表示为

(7)

2 耦合特性分析

基于古典控制理论,利用三回路过载驾驶仪设计俯仰和偏航通道,利用滚转驾驶仪设计滚转通道,按照滚转响应时间是俯仰通道的2倍及以上,侧向尽量快的原则进行设计。在驾驶仪设计完成后,将各项耦合代入设计好的独立三通道驾驶仪中进行仿真验证,假设导弹期望实现惯性坐标系下45°方向100 m·s-2的机动,则此时输入三通道驾驶仪的指令分别为:俯仰加速度指令ayc=100 m·s-2,偏航加速度指令azc=0 m·s-2,滚转角指令γc=45°。

以某飞行器气动数据为例进行仿真,飞行高度3 km,飞行速度为460 m/s(1.38Ma)的飞行状态时气动参数[10]为cωx=2.61,aβ=295,bδr=0.8,aωy=0.028,bβ=0.6,aδa=85,aωx=0.002 8,aδr=695,cωy=0.014,cβ=6 438,cδa=1 113。

通过对耦合特性的简要分析,将主要影响项加入到驾驶仪中进行仿真研究,分别引入运动学耦合、气动耦合和控制交叉耦合。

2.1 运动学耦合

根据BTT运动学方程可知,弹体坐标系下的俯仰和偏航动力学方程中分别含有运动学耦合项-ωxβ、ωxα,运动学耦合的产生是由于导弹作滚转运动产生的,在导弹的控制回路中运动学耦合的存在是必然的,这是由于导弹的控制回路是基于弹体坐标系工作的,而制导回路却不一定受运动学耦合的影响,这是由于制导回路工作在惯性系下导致的。

由于在BTT的控制模式下,尽量抑制侧滑角β,所以-ωxβ为小量,ωxα为主要影响因素,现将考虑偏航-滚转通道,仅以ωxα为输入项,分析导弹在固定攻角下,以常值ωx滚转时弹体特性。首先对仅以ωxα为输入项的侧向传函进行推导。

根据简化后的侧向方程式(8)对侧向传递函数进行推导,仅考虑攻角项对侧向的影响,即此时以ωxα为输入项进行传函推导[11]。

(8)

对上式进行拉式变换有:

(9)

(10)

对式(8)进行求解得到:

(11)

将式(11)代入式(9)得到:

(12)

当s→0时得到β/αωx的稳态值为aωy/(bβaωy+aβ)。

将式(12)代入式(9)中得到:

(13)

当s→0时得到ωy/αωx的稳态值为-aβ/(bβaωy+aβ)。

将气动数据aωy=0,bβ=0.6代入式(8)～式(13),以α=10°,ωx=45°/s作为输入进行仿真。

图1 侧滑角响应曲线

图2 偏航角速度响应曲线

根据理论分析和仿真对运动学耦合进行分析,BTT导弹气动外形决定aβ不为零,则导弹在有攻角情况下进行滚转时,必然带来侧向机动,产生侧滑角,这是BTT控制不希望产生的。但若采用先将攻角减为零,再进行滚转的运动策略,对于末导时间较短的情况,弹体则不能完成机动过程。所以BTT运动学耦合对导弹的控制有较大影响。

仅引入运动学耦合到三通道驾驶仪进行联合仿真,仿真图如图3、图4所示。

图3 侧滑角

从上图仿真结果可以看出,对于建立在弹体系下的控制回路,运动学耦合必然存在,且对控制回路设计产生影响,主要体现为耦合产生侧滑角,在驾驶仪可调整各通道间时间比值进行设计尽快消除侧滑角。

图4 弹体系下偏航加速度

2.2 气动耦合

对于此模型而言,气动耦合较小,只受斜吹力矩的影响。单独引入气动耦合分析其对BTT弹体的影响,通过对简化模型的分析可知,当只有气动耦合时,相对于只有偏航通道对滚转通道产生影响,其他通道之间没有相互作用。若想研究气动耦合影响,则需给定偏航通道一定输入,产生侧滑角进而使斜吹力矩对滚转通道产生影响。以azb=1 g为输入进行仿真,得到滚转通道响应对比如图5所示,对比得到有无耦合情况下滚转角速度响应曲线如图6。

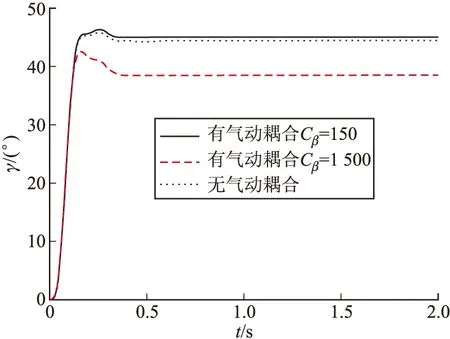
图5 滚转角曲线

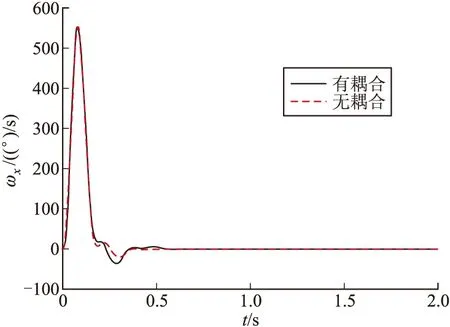
图6 滚转角速度曲线

通过仿真可得,对本模型而言气动耦合影响较小,由于气动耦合的加入对滚转角的调节时间和稳态增益都有影响,具体变化与气动导数cβ有关,随着cβ的增加耦合越严重,对滚转通道影响越明显。对cβ较大,气动耦合较大的模型需要进一步的设计,保证在引入耦合后自驾仪仍能完成控制需求。

2.3 控制交叉耦合

控制交叉耦合是指导弹在一个通道进行气动操纵控制会在另一个通道产生不希望的力和力矩,当导弹处于自由状态时(即攻角、侧滑角为0),控制面之间的交叉耦合通常较小可以忽略,但当导弹处于控制状态下(攻角、侧滑角不为0),通道间的控制交叉耦合就会大幅增加。对于面对称的BTT导弹而言,偏航-滚转间的控制交叉耦合远远大于俯仰-偏航通道,不可忽略。仅引入控制耦合到三通道驾驶仪进行仿真,仿真图如图7、图8所示。

图7 侧滑角响应曲线

图8 弹体系下偏航加速度

根据气动数据,分析控制交叉耦合aδa代表滚转舵对偏航耦合,耦合比为aδa/aδr=200/180=111%,接近1,表明滚转舵的运动对偏航影响较大,几乎接近直接传递或作用。cδr代表方向舵对滚转舵的耦合,耦合比为cδr/cδa=60/1 400≈4%为小量影响较小。对于此气动数据而言,滚转舵对偏航耦合严重,设计

结果需能减弱此耦合带来的影响。

3 结论

文中根据BTT导弹的运动学和动力学特点,在小扰动线性化假设下建立了BTT导弹的弹体模型,根据耦合特性进行解耦设计,分析了运动学耦合、动力学耦合和控制学交叉耦合的产生原理,并通过仿真分析了各耦合项对BTT导弹控制系统设计的影响。

在有攻角情况下,运动学耦合使得弹体在有攻角情况下滚转时,产生侧向机动,侧滑角显著增加,过渡过程变长,由此引发了偏航通道的振荡及响应时间变慢,对控制系统设计产生较大影响。所以BTT运动学耦合对导弹的控制有较大影响。气动耦合对滚转角的调节时间和稳态增益都有明显影响,控制系统设计前需对气动导数cβ进行分析。在考虑控制交叉耦合时需分析耦合比的影响,在控制系统设计时应减小其他通道对偏航通道的影响。

[1] 李秋月, 李忠应. 倾斜转弯导弹制导与控制系统评述 [J]. 北京航空航天大学学报, 1993(3): 75-80.

[2] 张頔, 林德福, 崔晓曦, 等. BTT控制弹体线性模型及传函推导 [J]. 弹箭与制导学报, 2013, 33(6): 34-37.

[3] Arrow A. An analysis of aerodynamic requirements for coordinated bank-to-turn autopilot, NASA-CR-3644 [R]. 1982.

[4] Emmert R T, Fought D E, Burye R L. BTT steering autopilot evaluation support, AFATL-TR-78-123, ADC01478L [R]. 1978.

[5] 钱杏芳, 林瑞雄, 赵亚男, 等. 导弹飞行力学 [M]. 北京: 北京理工大学出版社, 2006.

[6] 彭冠一. 防空导弹武器制导控制系统设计 [M]. 北京: 宇航出版社, 1996: 236-241.

[7] Garnell P. Guided weapon control systems [M]. Beijing: Beijing Institute of Technology, 2004.

[8] 孙宝彩. 巡航飞行导弹BTT自动驾驶仪设计方法研究 [D]. 北京: 北京理工大学, 2007.

[9] 林德福, 王辉, 王江, 等. 战术导弹自动驾驶仪设计与制导律分析 [M]. 北京: 北京理工大学出版社, 2012.

[10] John H. Blakelock. Automatic control of aircraft and missiles [M]. USA: A Wiley-Interscience Publication, 1991.

[11] 刘豹, 唐万生. 现代控制理论 [M]. 北京: 机械工业出版社, 2006.

Coupling Properties Analysis of Bank-to-turn Missile

ZHANG Di

(Beijing Electro-mechanical Institute, Beijing 100074, China)

According to kinematics and dynamics characters of bank-to-turn missile, the mathematical model of bank-to-turn missile was built, and the coupling model was decoupled. According to effect of coupling, the influences of kinematic coupling, aerodynamic coupling and cross-coupling control were analyzed, and the causes of the couplings were analyzed. The simulation illustrates influence of various coupling on control system. The influence of the sideslip was analyzed based on the characteristics of BTT. Research shows that the kinematic coupling and the cross-coupling control should be paid more attention for control system design. It is useful for control system design in the future.

bank-to-turn missile (BTT); kinematic coupling; aerodynamic coupling; cross-coupling control

2014-08-12

张頔(1989-),女,黑龙江哈尔滨人,工程师,硕士,研究方向:飞行器总体设计、制导与控制。

TJ760.3

A