运载火箭姿态的自抗扰控制器设计*
2015-04-17程昊宇
王 晔,程昊宇
(1 湖北工业大学电气与电子工程学院,武汉 430068;2 北京宇航系统工程研究所,北京 100076;3 北京航空航天大学航空科学与工程学院,北京 100191)
运载火箭姿态的自抗扰控制器设计*
王 晔1,2,程昊宇3
(1 湖北工业大学电气与电子工程学院,武汉 430068;2 北京宇航系统工程研究所,北京 100076;3 北京航空航天大学航空科学与工程学院,北京 100191)
为了抑制运载火箭自身结构参数变化和内外扰动对姿态控制精度和姿态稳定性的影响,设计了自抗扰控制器。通过跟踪微分器为期望姿态安排过渡过程,并提取其微分信号,然后利用扩张状态观测器,采用复合量测信息对系统的不确定项进行估计;设计姿态反馈控制器,利用扩张状态观测器估计的信号对不确定项进行实时补偿,实现对运载火箭的姿态控制。最后通过仿真说明了自抗扰控制器可以获得良好的动态性能、抗扰性和较强的鲁棒性。
运载火箭;姿态控制;自抗扰控制器;扩张状态观测器;鲁棒性
0 引言
随着航天技术的发展,运载火箭的构造越来越复杂,性能要求也越来越高,而姿态控制技术是确保运载火箭飞行成功的关键技术,传统的运载火箭姿态控制技术是采用比例微分+校正网络的控制方式[1],通过改变动静态增益和校正网络对火箭进行控制,但是火箭的模型一般是不能确切获知的,具有参数不确定性,而且火箭在飞行过程中普遍存在的内部结构干扰、风干扰等内外扰动会影响姿态控制系统的控制精度和性能,采用PD控制不易满足系统高性能的要求,因此,设计满足运载火箭的性能要求,能够解决非线性、强耦合特性问题,且对系统存在的内外不确定性具有鲁棒性的姿态控制器,成为运载火箭姿态控制研究的重要内容。
近年来,许多学者对火箭的姿态控制进行了研究[2-4],文献[3]采用自适应方法研究了火箭的姿态控制问题;文献[4]采用二阶滑模实现了运载火箭的姿态控制,在保证系统鲁棒性的前提下,有效的削弱了抖振现象,但是以上方法都依赖于火箭的精确模型,由于火箭模型复杂,在实际工程中很难获得精确的数学模型。
自抗扰控制器包括跟踪微分器(tracking differentiator, TD)、扩张状态观测器(extended state observer, ESO)、非线性反馈(nonlinear feedback, NF)等技术,具有不依赖于被控对象的精确模型、鲁棒性强、精度高、抗干扰能力强和算法简单等优点[6],在航空航天领域获得了广泛的应用[7-11]。文献[8]研究了航天器的高度控制问题,将滑模控制与自抗扰控制结合起来设计控制器,并与自适应滑模控制算法进行比较,仿真表明,自抗扰滑模算法具有较高的控制精度和较强的鲁棒性;文献[9]针对无人直升机航向通道扰动大的问题,设计了自抗扰算法来实现其高性能控制,并与常见的串级控制方法进行了对比分析。
由于运载火箭模型复杂,在飞行过程中会受到各种内外不确定性的影响,文中针对运载火箭姿态设计问题,设计了自抗扰控制器。首先以纵向通道为例建立了运载火箭小偏差姿态动力学模型,通过跟踪微分器安排过渡过程,柔化程序角信号并提供其微分信号,然后通过扩张状态观测器[11-13]对内外干扰进行估计,采用非线性姿态反馈控制器对干扰进行实时补偿,从而实现对火箭姿态的控制,最后通过仿真将文中设计的控制器与传统的PD控制进行对比,说明了自抗扰控制具有较强的鲁棒性和较高的控制精度。
1 模型描述
火箭动力学模型是在将火箭视为一维梁模型的基础上推导而来的。推导火箭动力学方程的文献较多,从建模原理和方法上看主要有两类,一类是牛顿-欧拉矢量力学方法,另一类是以拉格朗日方程为代表的分析力学方法。火箭姿态控制系统主要考虑的是姿态角偏差的消除,并使箭体按照选定的轨道和给定的程序角飞行,可以近似认为箭体姿态角偏差暂态过程中方程系数是固定不变的,可以采用“固化系数法”对火箭进行建模和分析。文中以某型火箭为例,给出俯仰通道刚体与弹性运动方程,其中,刚体运动方程为:

(1)

(2)
Δφ=Δα+Δθ
(3)
弹性振动方程为:
(4)
惯组和速率陀螺测量方程为:
(5)
(6)
其中:b3为控制力矩系数;b″3为摆动发动机惯性力矩系数;i=1,2,…,n为弹性振动阶次,D3i为广义控制力系数,D″3i为摆动发动机广义惯性力系数;δφ为俯仰通道综合控制摆角,其余参数和定义可参考文献[14]。
注:偏航通道控制器设计和滚动通道控制器设计与俯仰通道控制器设计类似,这里不再赘述。
2 自抗扰控制器设计
文中提出的自抗扰控制器由跟踪微分器、扩张状态观测器和非线性反馈控制器三部分组成。自抗扰控制对模型依赖程度较低,并且对于系统中的内外干扰具有较好的抑制作用,非常适合运载火箭这类动态特性复杂,且存在各种不确定性的非线性系统,因此,文中以俯仰通道为例,设计自抗扰控制器,需要指出的是,火箭3个通道之间虽然存在耦合,但是自抗扰控制器可以完全解决耦合的问题,将耦合项当作系统的内部扰动,同环境干扰力矩一起,均作为对整个系统的扰动,利用ESO进行实时估计并补偿。整个系统的结构图如图1所示。
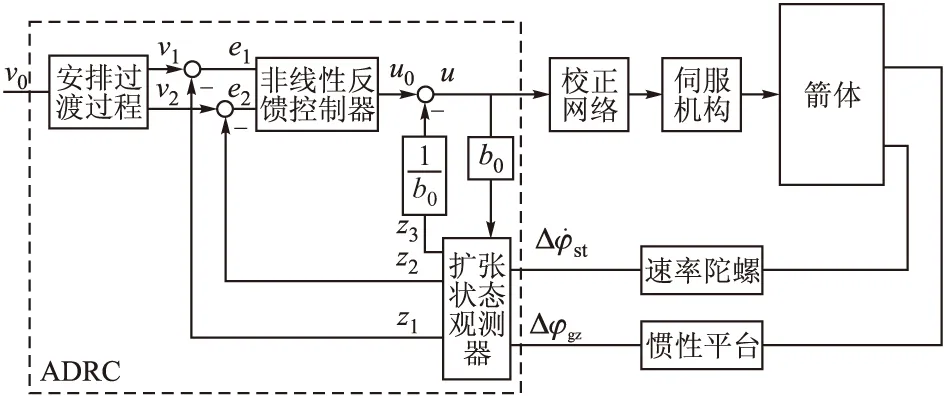
图1 火箭自抗扰控制系统结构
2.1 安排过渡过程
事先安排过渡过程是解决超调与快速性矛盾的一种很有效的办法,还可以使给定的反馈增益所能适应的对象参数范围扩大,文中采用如下所示跟踪微分器[15]实现安排过渡过程,柔化程序角信号,减小其突变量:
(7)
式中:非线性函数fhan(·)为最速控制综合函数,其算法公式如下所示:
(8)
其中:v0为控制输入,v1为控制输入v0的跟踪信号,v2为v1的微分信号,可近似当做v0;fhan(·)函数的主要作用是在给定加速度上限的条件下,让v1最快且无抖振的跟踪程序角信号v0,包含r和h两个参数,其中,h为系统的采样周期,r为可调参数,若r越大,则v1跟踪v0越快,因此把r称为“快速因子”,可以根据过渡过程的快慢以及系统的承受能力来决定。
通过式(7)所示的跟踪微分器来安排过渡过程,可以用较为光滑的信号v1代替突变的程序角信号v0,并且得到其微分值,然后与反馈信号作差,进而得到较为柔和的误差及其微分信号。
2.2 扩张状态观测器设计
由于系统的模型不可避免的存在偏差,而且火箭在飞行过程中由于飞行高度、飞行速度、大气环境的变化以及火箭内部结构干扰的影响,导致箭体姿态动力学模型参数存在很大程度的不确定性,而且柔性火箭的姿态控制系统设计需要考虑箭体弹性振动的影响,而弹性振动频率也具有不确定性。文中综合利用惯组和速率陀螺的测量信息,采用复合误差对状态和干扰进行估计和补偿,简化了设计。定义复合观测误差为:
(9)
设计扩张状态观测器如下:
(10)
其中:z1、z2分别为俯仰角和俯仰角速率的估计;z3为内外不确定项的估计;κ、λ为适当选取的大于零的常数;βi(i=1,2,3)为ESO的参数,可以根据观测效果进行调整;b0是决定补偿强弱的“补偿因子”,作为可调参数来使用;fal(·)为非线性函数,δ1为设定值,μ1、μ2为其参数,可以根据误差大小来调整控制增益,其表达式为:
(11)
利用扩张状态观测器可以对系统中的扰动进行很好的估计,然后反馈至控制器进行补偿。
2.3 姿态反馈控制器设计
将跟踪微分器输出的程序角及其微分信号与扩张状态观测器输出的俯仰角和俯仰角速率的估计信号作差,并对扩张状态观测器估计的不确定项进行实时补偿,实现自抗扰的功能,因此设计如下形式的误差反馈律:
其中:误差信号e1=v1-z1;误差微分信号e2=v2-z2;kp、kd分别为控制律的比例增益和微分增益,为可调参数;fal(·)函数如前所述,当0<μ3<1,u0中的比例环节fal(e1,μ3,δ2)是控制工程界的一个经验知识:“大误差,小增益;小误差,大增益”的数学拟合,采用一个简单的非线性结构fal(·)描述了这一经验知识,对于微分环节fal(e2,μ4,δ2)则要求微分误差小时微分增益也小,微分误差大时微分增益也大,因此取μ4>1,这样使得接近稳态时微分作用变小。
3 仿真结果与分析
文中以某型号火箭发射过程中相关秒点的系统参数为例,考虑一阶弹性振动,即i=1,对系统进行仿真,标称模型的参数取值如下所示:
c1=0.163;c1p=0.001 3;c2=0.093;c3=0.04;c″3=4.937×10-5;c4=-5×10-4;b1=0.046 5;b2=-0.042 1;b3=0.567 4;b″3=0.567 6;b11=6.812×10-4;ζ1=0.005;ω1=8.5;D11=-1.912 1;D21=7.235 7;D31=16.428 6;D″31=0.021 7。
自抗扰控制器参数为:β1=5.2,β2=40,β3=1.9,kp=0.7,kd=1.8,μ1=0.25,μ2=0.25,μ3=0.35,μ4=1.1,δ1=0.06,δ2=0.05,b0=0.8。
分别在以下两种情况下对系统进行仿真,并将传统的PD控制与自抗扰控制进行对比:
情况1:标称情况下,俯仰角存在5°度的初始偏差;
通过图2~图5所示的仿真可以看出,在存在内外干扰的情况下,采用自抗扰控制器,比传统动态增益+静态增益的控制方法具有更强的抗扰性,说明了自抗扰控制器有效地对干扰进行了实时补偿,满足了系统性能的要求。
情况1的仿真结果如图2~图3所示。
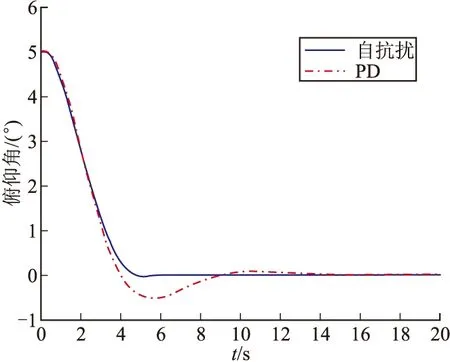
图2 情况1俯仰角响应曲线
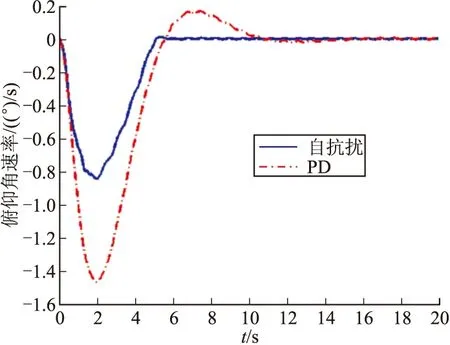
图3 情况1俯仰角速率响应曲线
存在不确定情况下的仿真曲线如图4~图5所示。

图4 情况2俯仰角响应曲线

图5 情况2俯仰角速率响应曲线
4 结论
1)采用扩张状态观测器有效估计了系统受到的内外扰动,且不依赖于精确的运载火箭模型。
2)利用非线性反馈技术对扩张状态观测器估计的扰动信息进行实时补偿,并采用跟踪微分器柔化了程序角信号。
3)充分利用了惯组和速率陀螺的信息,通过复合量测信息,设计了单回路姿态控制系统,简化了系统的结构。
4)通过仿真与传统PD控制进行对比,说明了自抗扰控制器具有鲁棒性好,控制精度高的优点。
[1] 徐延万. 液体导弹与运载火箭系列: 控制系统(上册) [M]. 北京: 宇航出版社, 2005.
[2] Roshannian J, Saleh A R, Jahed-Motlagh M R. On the design of adaptive autopilots for a launch vehicle [J]. ImechE Part I: J System and Control Engineering, 2007, 221: 27-38.
[3] Choong-Seok Oh, Hyochoong Bang, Chang-Su Park. Attitude control of a flexible launch vehicle using an adaptive notch filter: ground experiment [J]. Control Engineering Practice, 2008, 16: 30-42.
[4] 王青, 王昭, 董朝阳. 一种基于二阶滑模的柔性运载火箭姿态控制 [J]. 系统仿真学报, 2009, 21(7): 2006-2009.
[5] Han Jingqing. From PID to active disturbance rejection control [J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[6] Li Shunli, Yang Xu, Yang Di. Active disturbance rejection control for high pointing accuracy and rotation speed [J]. Automatica, 2009, 45(8): 1854-1860.
[7] Wang Chunming, Xia Yuanqing, Fu Mengyin, et al. Application of active disturbance rejection control in tank gun control system [J]. Journal of The Franklin Institute, 2014, 351(4): 2299-2314.
[8] Xia Yuanqing, Zhu Zheng, Fu Mengyin, et al. Attitude tracking of rigid spacecraft with bounded disturbances [J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 647-659.
[9] 方勇纯, 申辉, 孙秀云, 等. 无人直升机航向自抗扰控制 [J]. 控制理论与应用, 2013, 31(2): 238-243.
[10] 康莹, 李东海, 老大中. 航天器姿态的自抗扰控制与滑模控制的性能比较 [J]. 控制理论与应用, 2013, 30(12): 1623-1629.
[11] Zheng Zhu, Dong Xu, Liu Jingmeng, et al. Missile guidance law based on extended state observer [J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5882-5891.
[12] Guo Baozhu, Zhao Zhiliang. On the convergence of an extended state observer for nonlinear system with uncertainty [J]. Systems & Control Letters, 2011, 60(6): 420-430.
[13] Guo Baozhu, Zhao Zhiliang. On convergence of non-linear extended state observer for multi-input multi-output system with uncertainty [J]. IET Control Theory and Applications, 2012, 6(15): 2375-2386.
[14] 徐延万. 弹道导弹、运载火箭控制系统设计与分析 [M]. 北京: 宇航出版社, 1999: 63-65.
[15] Guo Baozhu, Zhao Zhiliang. On convergence of tracking differentiator [J]. International Journal of Control, 2011, 84(4): 693-701.
Active Disturbance Rejection Control of Attitude for Launch Vehicle
WANG Ye1,2,CHENG Haoyu3
(1 School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China;2 Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China;3 School of Aeronautic Science and Technology, BUAA, Beijing 100191, China)
A novel active disturbance rejection controller(ADRC) of attitude was designed to attenuate effect of parameter variation and disturbances of launch vehicle on attitude control accuracy and stability. A tracking differentiator was proposed to arrange transient dynamics of desired attitude and provide differential signal of the attitude, then an extended state observer was designed to estimate and compensate impact of parametric uncertainties and disturbances by taking full advantage of information of gyros and attitude sensors. An attitude feedback controller was designed to realize attitude control by compensating the disturbances from the extended state observer. Simulation results show that ADRC exhibits better dynamic performance, higher ability and stronger robustness against external disturbance and parameter uncertainty.
launch vehicle; attitude control; active disturbance rejection control; extended state observer; robustness
2014-07-07
国家自然科学基金(61273083)资助
王晔(1970-),男,北京人,硕士研究生,研究方向:鲁棒控制,自抗扰控制。
O232;V448
A
