火箭弹脉冲修正扰动运动仿真*

游培寒,缪 昕,乔治军,祝逢春

(1 95856部队,南京 210000;2解放军理工大学理学院,南京 210007)

火箭弹脉冲修正扰动运动仿真*

游培寒1,缪 昕2,乔治军1,祝逢春1

(1 95856部队,南京 210000;2解放军理工大学理学院,南京 210007)

为了构建火箭弹扰动运动半实物仿真,需要对火箭弹运动进行建模和简化。文中分析影响火箭弹弹体扰动运动的主要因素,构建脉冲发动机工作时弹体扰动方程。利用火箭弹弹体与弹道夹角较小,以及脉冲发动机冲量方向和弹道垂直等特征,对扰动运动方程进行简化,推导出纵向和侧向弹体扰动运动模型,得到扰动运动衰减系数和弹体振荡频率的相关计算公式。仿真结果表明,新扰动运动模型能够模拟火箭弹扰动运动。

脉冲发动机修正;扰动运动;弹道仿真

0 概述

弹体扰动运动仿真对火箭弹侧姿系统验证、修正方法研究等都有重要意义。文中以脉冲发动机修正为例,设计了一种能够在实验室环境下进行脉冲修正扰动运动仿真的建模方法。由于脉冲发动机工作时间短、冲量相对恒定,可以利用脉冲函数模拟其工作过程,利用拉氏变换对纵向和侧向的扰动运动进行了推导,得出两个方向的解析解,及扰动衰减系数和振荡频率等参数的计算方法,利用Simulink软件进行扰动运动建模,建模运算结果与6自由度火箭弹弹体运动方程计算结果基本一致。文中第二部分介绍纵向和侧向扰动运动方程;第三部分推导扰动运动的解析解并分析扰动运动各部分组成;第四部分介绍利用Simulink设计的火箭弹扰动运动模型,第五部分给出部分仿真结果。

1 纵向和侧向脉冲扰动方程

假设火箭弹纵向脉冲修正时,弹体没有侧滑,则根据文献[4],弹体纵向运动方程可以简化为:

(1)

其中:X为阻力;Y为升力;G为重力;Fmc为脉冲修正力;Lmc为脉冲修正力臂长度;v为火箭弹速度标量;m为质量;θ为速度俯仰角;ϑ为弹体俯仰角;α为攻角;wz为俯仰角速度;Jz为俯仰转动惯量;Mz是俯仰力矩。根据火箭弹的气动特性,有如下关系:

(2)

(3)

将式(2)、式(3)代入式(1),可得到俯仰扰动运动方程为:

(4)

同理,可以推导出侧向扰动运动方程,其中Jz为侧向转动惯量,由于弹体轴向对称,有Jz=Jy,ψ是弹体航向角,ψv是速度航向角,wy是航向角速度,β是

侧滑角。

(5)

2 纵向和侧向运动解析

2.1 纵向脉冲扰动解析

对式(4)进行拉氏变换得到:

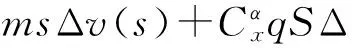
Fmc(s)

Jys2Δϑ(s)-mwqSLsΔϑ(s)-mαqSLΔϑ(s)+

mαqSLΔθ(s)=LmcFmc(s)

(6)

2.1.1 速度俯仰角的解析解

从式(6)可得:

则可以推导出:

Δθ(s)=

θ0取值较小的情况下可以忽略mαqSLGsinθ0和mwqSLGsinθ0则有:

设

纵向俯仰角扰动各部分放大系数为:

得到速度俯仰角扰动运动解析解为:

(7a)

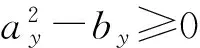
除了施工现场的安全检查之外，施工技术的安全检查很容易被忽视，导致很多建筑施工企业未能及时发现施工技术的缺陷，不仅不利于整个工程的建设质量，而且还给施工项目带来巨大的安全隐患，不利于整个项目的顺利开展。

(7b)

式中：sinh()是双曲正弦函数,ay为衰减系数,Ry1为纵

向扰动的振荡频率。

2.1.2 弹体俯仰角的解析解

扰动运动各部分放大系数为:

得到弹体俯仰角的扰动运动解析解为:

(8a)

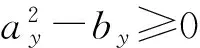
(8b)

2.2 侧向脉冲扰动解析

对式(5)进行拉氏变换得到:

Jycosϑs2Δψ(s)-mwcosϑqSLsΔψ-mαqSLΔψ(s)+

mαqSLΔψv(s)=Fmc(s)Lmc

(9)

2.2.1 速度航向角的解析解

Δψv(s)=

设:

因为cosθ=cosϑ=1

可以发现,当俯仰角较小时,侧向扰动的各部分放大系数与纵向扰动一致,得到速度航向角扰动运动解析解为:

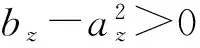
(10a)

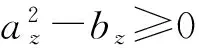
(10b)

2.2.2 弹体航向角的解析解

Δψ(s)=

得到弹体航向角扰动运动解析解为:

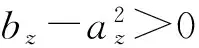
(11a)

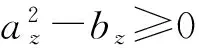
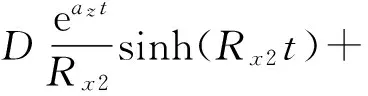
(11b)

3 Simulink建模

根据上文推导可以得到纵向和侧向扰动运动的Simulink模型如图1和图2所示,其中建模参数为:

mα=-2.143 0 rad-1

mw=-0.018 8 rad-1

v0=554 m/s

m=3.56 kg

θ0=0.112 4°

4 仿真结果

将文中扰动建模计算结果与火箭弹6自由度弹道仿真结果进行了对比,两者扰动运动结果如图3～图10所示,通过比较可以发现,两者结果基本一致。

图1 火箭弹纵向扰动运动模型

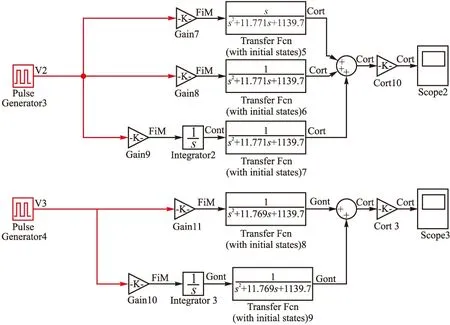
图2 火箭弹侧向扰动运动模型

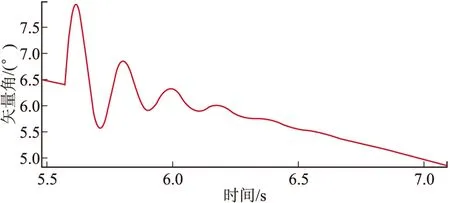
图3 纵向弹体矢量角的扰动运动

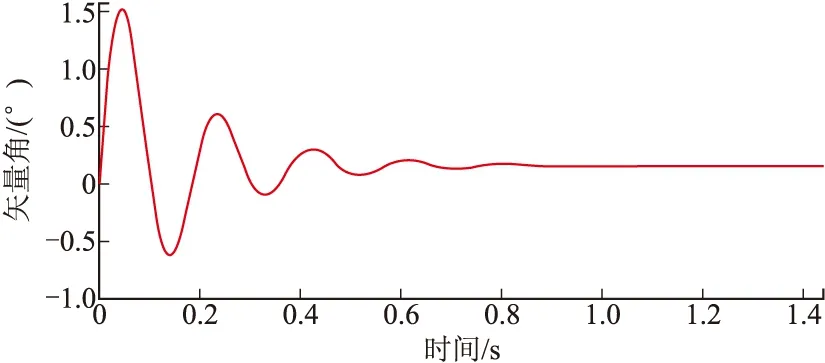
图4 纵向弹体矢量角的仿真结果

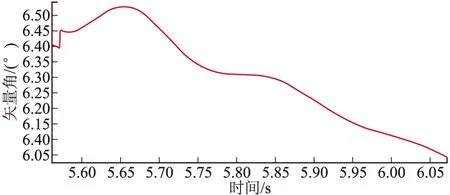
图5 纵向速度矢量角的扰动运动

图6 纵向速度矢量角的仿真结果

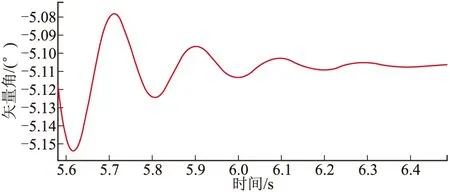
图7 侧向弹体矢量角的扰动运动

图8 侧向弹体矢量角的仿真结果

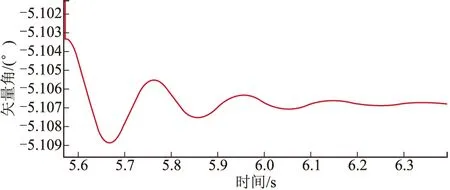
图9 侧向速度矢量角的扰动运动

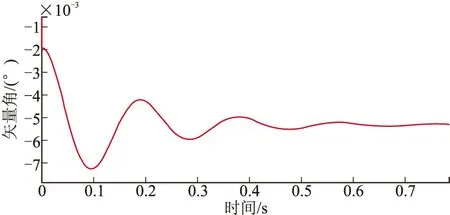
图10 侧向速度矢量角的仿真结果

5 结论

文中提出了一种利用Simulink构建火箭弹脉冲修正扰动运动模型的方法,利用火箭弹弹体与弹道夹角较小,以及脉冲发动机冲量方向和弹轴方向垂直等特征对火箭弹扰动运动方程进行了简化,并计算了弹体和速度矢量纵向和侧向扰动运动解析解。仿真结果表明,文中提出的方法能够模拟火箭弹在空中进行脉冲修正时的扰动运动,可以应用于实验室环境下的各种半实物仿真和扰动弹道计算中。

[1] 姚文进, 王晓鸣, 高旭东, 等. 弹道修正弹脉冲修正机构简易控制方法 [J]. 弹道学报, 2007, 19(3): 19-22.

[2] 曹小兵, 王中原, 史金光, 等. 火箭脉冲矢量控制弹道特性分析 [J]. 弹箭与制导学报, 2005, 25(3): 67-69.

[3] 赵捍东. 脉冲发动机提供控制力的火箭弹道修正理论及技术研究 [D]. 南京: 南京理工大学, 2008.

[4] 钱杏芳, 林瑞雄, 赵亚罗. 导弹飞行力学 [M]. 北京: 北京理工大学出版社, 2000.

[5] Jan J Tuma，Ronald A Walsh. 工程数学手册 [M]. 欧阳芳锐，张玉平，译. 4版. 北京: 科学出版社, 2002.

A Rocket Bomb Pulse Jets Correction Perturbed Motion Simulation

YOU Peihan1,MIAO Xin2,QIAO Zhijun1,ZHU Fengchun1

(1 No.95856 Unit, Nanjing 210000, China; 2 PLA University of Science and Technology, Nanjing 210007, China)

For constructing rocket bomb’s perturbed motion semi-physical simulation, we should construct and simplify bomb’s flight motion model. In this paper, main factors that influence rocket bomb’s perturbed motion were analysed, pulse jets correction perturbed motion equations were constructed. Since the attack angle between velocity and bomb’s body is small and negligible, and pulse jets correction is perpendicular to the trajectory, we can simplify the perturbed motion equations, and get the model of rocket bomb’s perturbed motion, get attenuation coefficient and oscillation frequency’s calculation method. Simulation results show that the new simplified model can simulate rocket bomb’s perturbed motion and get similar result with 6-DOF trajectory simulation.

pulse jet correction; perturbed motion; trajectory simulation

2014-06-25

游培寒(1978-),男,江苏南京人,工程师,博士,研究方向:航空弹药与制导控制。

V216.7

A