低成本MIMU/GPS车载组合测量系统的导航算法设计*
2015-04-17吕妍红
刘 江,吕妍红
(北京航空航天大学,北京 100191)
低成本MIMU/GPS车载组合测量系统的导航算法设计*
刘 江,吕妍红
(北京航空航天大学,北京 100191)
文中的组合测量系统用于测量汽车的位置、速度和姿态信息,为提高测量精度,文中设计的导航算法为:系统做近似直线运动时,采用基于位置、速度、航向组合的导航算法;系统做转弯运动时,采用基于位置、速度组合的导航算法。实际跑车实验表明,系统位置精度为3 m(CEP)、速度精度为0.25 m/s、航向精度为1°,相对单纯的位置、速度组合导航算法,系统的测量精度有所提高,尤其航向测量精度提高了1倍,从而说明文中所述导航算法的有效性。
微惯性测量单元;航向组合;卡尔曼滤波;组合导航
0 引言
惯导系统作为一种重要的自主式导航设备,其具有隐蔽性好、抗干扰、不受气象条件限制、输出导航参数全面且输出频率高的优点,已广泛应用于航空、航天、航海和陆地导航中[1-2]。但是,惯导系统高昂的成本,使其主要用于国防领域,在民用领域的应用很少。惯导系统的成本主要受限于惯性器件的成本,特别是陀螺仪的成本。近年来,惯性器件特别是MEMS陀螺仪和加速度计取得了非常显著的进步,其以尺寸小、重量轻、低成本、微功耗、可靠性高、易于批量加工、耐振动和冲击等优点而被大量用于许多民用领域。目前基于惯性测量、卫星测量及其组合测量特别是低成本的MEMS陀螺仪和加速度计与GPS的组合测量在汽车位置姿态测量中应用发展迅速[3]。
SINS/GPS的组合方式包括浅组合、紧组合和深组合,其中浅组合由于工程实现容易,因而应用广泛[4]。浅组合是基于位置、速度量测构建卡尔曼滤波,其对惯导系统位置、速度误差具有很好的抑制作用,但对航向误差的抑制作用小,航向仍会因误差积累而发散。文中将在基于位置、速度组合的导航算法基础上,再添加基于位置、速度、航向组合的导航算法;根据当前系统的运动状态,实现两种导航算法之间的切换,以提高对汽车位置、速度、姿态的测量精度。
1 传感器简介
系统采用的MIMU为荷兰Xsens Technologies公司的MTI-10 IMU,其集成了3个单轴的MEMS陀螺仪、两个双轴MEMS加速度计和一个温度传感器;其MEMS陀螺仪的实测零偏稳定性为100°/h,长期零偏重复性为0.2°/s;其MEMS加速度计的实测零偏稳定性为80μg,长期零偏重复性为0.03 m/s2。
系统采用的GPS接收机为星网宇达科技开发有限公司的XW-GPS1001卫星接收机,其标称的定位精度为2.5 m(CEP)、速度精度为0.1 m/s,其输出的航向为轨迹航向。轨迹航向是根据相邻两个时刻的位置坐标计算得到的,而一般导航系统输出航向为速度航向。由此可知:当系统做近似直线运动时,GPS接收机输出航向是可信的;当系统做转弯运动时,其输出航向是不可信的。
2 组合导航算法设计
设计基于卡尔曼滤波的组合导航算法时,需要建立描述组合导航系统动态特性的系统状态方程和反映量测与状态关系的量测方程[5],下面将分别予以介绍。
2.1 系统状态方程
系统的状态向量选为12维,包括3个平台误差角,东向、北向速度误差,纬度、经度误差,X、Y、Z轴陀螺随机常值漂移和X、Y轴加计随机常值零偏。根据惯导系统的平台误差角方程、速度误差方程和位置误差方程[5],并将MEMS惯性器件误差简化为随机常值误差与白噪声之和,可以写出系统状态方程为:

(1)式中:
其中,FN为对应于SINS的7个误差参数(3个姿态误差,2个速度误差,2个位置误差)的系统动态矩阵,其非零元素为:



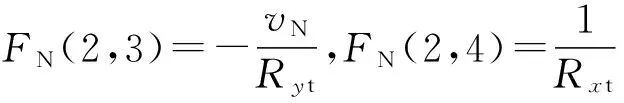
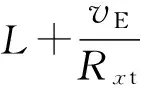

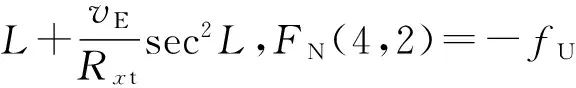
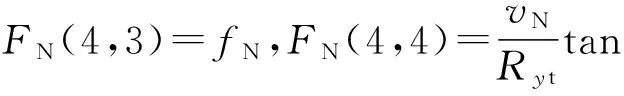


FN(5,1)=fU,FN(5,3)=-fE,

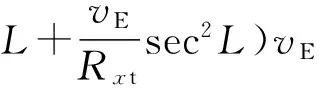


2.2 基于位置、速度组合的量测方程
系统基于位置、速度组合的量测向量的维数为4,包括东向、北向速度误差量测量,东向、北向位置误差量测量。量测向量的计算式为
(2)

(3)式中:
其中:ME、MN分别为GPS量测的东向、北向速度误差,NN、NE分别为GPS量测的东向、北向位置误差。
2.3 基于位置、速度、航向组合的量测方程
系统基于位置、速度、航向组合的量测向量的维数为5,即在前述位置、速度组合的基础上添加航向误差量测量,其位置、速度误差量测方程同2.2,下面详细推导航向误差量测方程。
由系统三轴姿态角可得到姿态矩阵为:
(4)
由坐标变换有:
(5)
式中:
根据式(4)、式(5)可得:
(6)
设捷联惯导系统输出的航向角为ψSINS=ψ+δψ,则根据式(4)、式(6)可得:
(7)
将式(7)的右边按泰勒级数展开并忽略误差角的二次项得:
(8)
由于δψ是一个小量,可以近似认为tanδψ=δψ,则式(7)的左边可写为:
(9)
将式(9)按泰勒级数展开并忽略误差角的二次项,得:
(10)
另外,有:
(11)
连同式(8)、式(10)、式(11)可得:
(12)
式(12)即为航向角误差量测方程。
需要注意的是:在计算航向角误差量测时,不能简单地由ψSINS与ψGPS作差得到。航向角误差的方向定义为:以ψGPS按小角度逆时针转到ψSINS为正,以ψGPS按小角度顺时针转到ψSINS为负。其具体计算流程为:
step1将ψSINS和ψGPS的定义均转换为从北向算起、逆时针转动一周的变化范围为[0°,360°);
step2计算航向角误差δψ=ψSINS-ψGPS;
step3若ψSINS指示系统方位为北偏西,而ψGPS指示北偏东,则修正航向误差角δψ=δψ+2π,转step5;
step4若ψSINS指示系统方位为北偏东,而ψGPS指示北偏西,则修正航向误差角δψ=δψ-2π;
step5结束。
2.4 两种组合导航算法的切换条件
XW-GPS1001输出的航向为轨迹航向,即当系统做近似直线运动时,航向是可信的;当系统做转弯运动时,航向是不可信的。根据此特性,确定两种组合导航算法的切换条件为:当|ωz|<2°/s(ωz为系统转弯角速度)时,采用基于位置、速度、航向组合的导航算法;否则,采用基于位置、速度组合的导航算法。
3 跑车实验与结果分析
为验证文中提出的导航算法的有效性,进行了实际跑车实验。实验过程中,在保存系统输出的数据的同时,还保存NovAtel公司的DL-V3型GPS接收机输出的导航数据,其定位精度为1.5 m(CEP)、速度精度为0.03 m/s。在评价系统测量精度时,将以其输出数据作为参考基准。
跑车实验重复进行3次,图1~图3给出了第一次跑车实验的测量效果。使用第一次跑车实验数据,离线进行基于位置、速度组合的导航解算,其航向测量效果如图4所示,两种组合导航算法的测量精度对比如表1所示(导航算法1为文中所述导航算法,导航算法2为只采用位置、速度组合的导航算法)。由表1可知:相对单纯的位置、速度组合导航算法,采用文中所述的导航算法,系统的位置、速度、航向测量精度均有所提高,尤其航向测量精度提高了1倍。
采用文中所述导航算法,系统3次实验的测量精度如表2所示,由表2可知:系统的位置精度为3 m(CEP),速度精度(1σ)为0.25 m/s,航向精度(1σ)为1°,从而说明了导航算法的有效性。

图1 位置误差曲线

图2 速度误差曲线

图3 航向及航向误差曲线1
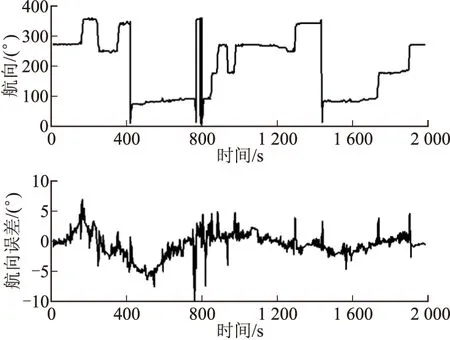
图4 航向及航向误差曲线2

导航算法位置精度/m速度精度/(m/s)航向精度/(°)12.87330.20220.962623.56780.21032.0309
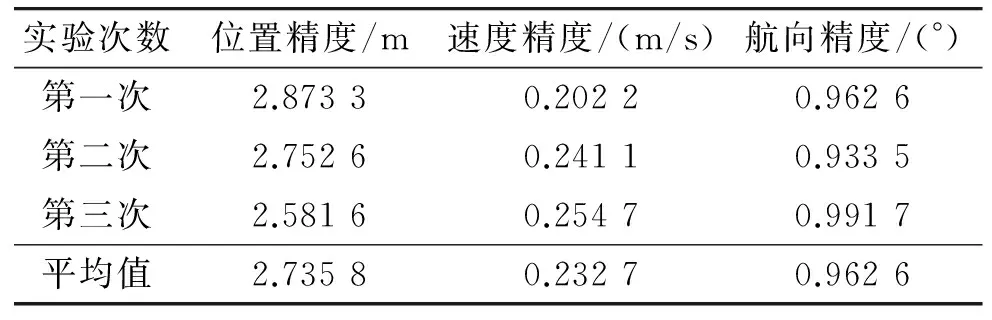
表2 系统测量精度
4 结论
文中针对低精度MIMU和GPS组合的测量技术在车载测量系统中的应用,提出在基于位置、速度组合的导航算法基础上,再添加基于位置、速度、航向组合的导航算法,根据当前系统的运动状态,实现两种导航算法之间的切换,以提高对汽车位置、速度、姿态的测量精度。通过进行实际跑车实验,以NovAtel公司的DL-V3型GPS接收机输出的数据作为参考基准,得到系统的位置精度为3 m(CEP),速度精度为0.25 m/s,航向精度为1°。相对采用单纯的位置、速度组合导航算法,采用文中所述的导航算法,系统的位置、速度、航向测量精度均有所提高,尤其航向测量精度提高了1倍。实验结果表明,文中所述的导航算法是有效的。
[1] 杨艳娟, 卞鸿巍, 田蔚风, 等. 一种新的INS/GPS组合导航技术 [J]. 中国惯性技术学报, 2004, 12(2): 23-26.
[2] 以光衢. 惯性导航原理 [M]. 北京: 航空工业出版社, 1987.
[3] 张小龙. 车辆主动安全性能道路试验系统及评价方法研究 [D]. 南京: 东南大学, 2006.
[4] 李倩. GPS/INS组合导航系统研究及实现 [D]. 上海: 上海交通大学, 2010.
[5] 秦永元, 张洪钺,汪叔华. 卡尔曼滤波与组合导航原理 [M]. 2版. 西安: 西北工业大学出版社, 2012.
Navigation Algorithm Design on Low-cost MIMU/GPS Integrated Measurement System for Vehicles
LIU Jiang,LYU Yanhong
(Beijing University of Aeronautics and Astronautics, Beijing 100191, China)
Integrated measurement system is used to measure vehicle’s position, velocity and attitude. To improve the measurement accuracy, a navigation algorithm is designed as follows:the algorithm based on position, velocity and yaw integration is used when the system is moving approximate linearly; If the system is turning, the algorithm based on position and velocity integration is applied. The car experiments show that the system’s measurement accuracy of positon is 3 m(CEP), that of velocity is 0.25 m/s and that of yaw is 1°. Compared with the navigation algorithm simply based on position and velocity integration, the designed navigation algorithm can achieve more accurate measurement. Especially, the measurement accuracy of yaw is doubling. The results indicate that the navigation algorithm designed is available.
micro-inertial measurement unit; yaw integration; Kalman filter; integrated navigation
2014-07-30
刘江(1989-),男,湖南人,硕士研究生,研究方向:惯性导航、组合导航。
V249.322
A
